Theory of Games has an impressive development during the last 70 years both as a domain of applied mathematics and a part of various important domains of human activity. It's somewhat strange that Mathematica doesn't include any functionality related to game theory. Our project intends to initiate a game theory Mathematica package.
At the first initiation stage of the project development, we consider strategic finite (multi-matrix) games and some solution concepts: Nash equilibrium, Stackelberg equilibrium, and MaxMin strategies:
Game statement
A strategic game is defined by the tuple: $$\Gamma = \langle N, \{X_i\}_{i\in N}, \{f_i (x)\}_{i\in N}\rangle,$$ where $N=\{1,2,...,n\}$ is a set of players, $X_i$ is a set of strategies of player $i\in N$ and $f_i:X\rightarrow R$ is a player's $i\in N$ payoff function defined on the Cartesian product $X = \times_{i \in N} X_i$. Elements of $X$ are called outcomes of the game (strategy profiles).
An outcome $x^*\in X$ of is a Nash equilibrium (shortly NE) of $\Gamma$ if $$f_i ( x_i, x_{-i}^*) \le f_i ( x^*_i, x_{-i}^* ), \forall x_i \in X_i,\,\, \forall i \in N,$$ where $$x_{-i}^* = (x^*_1, x^*_2, ..., x^*_{i-1}, x^*_{i+1}, ..., x^*_n),$$ $$x_{-i}^* \in X_{-i}=X_1 \times X_2 \times ... \times X_{i-1} \times X_{i+1} \times ... \times X_n,$$ $$(x_i,x_{-i}^*) = (x^*_1, x^*_2, ..., x^*_{i-1},x_i, x^*_{i+1}, ..., x^*_n)\in X.$$
We study Nash equilibrium sets as an intersection of best response mapping graphs [5,1, 2], i.e. the intersection of the sets: $$Gr_i=\{(x_i,x_{-i})\in X: x_{-i}\in X_{-i}, x_i\in {\rm Arg}\max_{x_i\in X_i} f_i(x_i,x_{-i})\},\,\, i\in N.$$
Theorem 1. The outcome $x^*\in X$ is a Nash equilibrium if and only if $x^*\in \bigcap_{i \in N}Gr_i$.
Theorem 1 stands for a main method that we will use to find Nash equilibrium set. So, we are looking to finding Nash equilibrium sets as the intersection of best response mapping graphs, both in pure and mixed strategy games.
Package design
We have designed package structure and features that have to be applied to all its functions, their titles and options. Main functions of the package a GameTheory[] and GameTheoryPlot[]. There is an idea to recall them GameSolve[] and GameSolvePlot[]. Formal parameters of the functions are initial data of the games, as well all the concepts that specifies a concrete game theory problem:
testOptionValue["Criteria" -> crit, {"Maximize", "Minimize"}];
testOptionValue["Strategy" -> type, {"Pure", "Mixed"}];
testOptionValue["Concept" -> concept, {"NashEquilibrium", "MaxMin", "StackelbergEquilibrium"}]
We have created algorithms and corresponding codes that solve problems of Nash equilibrium set finding, as well as MaxMin solutions computing. In this context we need to mention the following functions:
pureNashEquilibria[matr_] := ...
maxMin[matr_] :=...
pureStackelbergEquilibria[matr_] :=...
We have also programmed the code that solves two-matrix mixed strategy games.
mixedNashEquilibria[m_] := ...
The package includes, withal, a function that plot Nash equilibrium set in $2\times 2$ mixed strategy games.
game2x2Plot[m_]:= ...
Some private functions and their application
For the problem of Nash equilibrium set computing the main function is:
bestResponse[m_]:=With[{ind=indexSets[Dimensions[m[[1]]]]},
Intersection@@Table[
Flatten[
Thread/@Table[
Replace[i, All:>maxPositions@m[[player,Sequence@@i]], {1}],
{i, Tuples[ind[[player]]]}
],
1
],
{player, Length[m]}
]
]
The notation m is for payoff matrices of the players. Length[m] gives the number of players. Tuples[] gives all possible tuples formed by player strategies. maxPositions[] gives positions on which maximal values are obtained. The intersection of all Length[m] lists of players offers the set of Nash equilibria.
In practice, this function is called by GameTheory[] as in the following examples:
In[1]:= Clear[a, b]
a = {{2, 2, 3}, {7, 2, 2}, {1, 1, 4}};
b = {{5, 6, 1}, {5, 2, 3}, {3, 5, 7}};
MatrixForm /@ {a, b};
In[2]:= GameTheory[{a, b}, Method -> {"Criteria" -> "Maximize", "Concept" -> "NashEquilibrium", "Strategy" -> "Pure"}]
Out[2]= {<|"Player 1" -> 1, "Player 2" -> 2|> -> {2, 6}, <|"Player 1" -> 2, "Player 2" -> 1|> -> {7, 5}, <|"Player 1" -> 3, "Player 2" -> 3|> -> {4, 7}}
Another private function is:
(* ------ MaxMin strategies ------ *)
maxMin[matr_]:=Module[{dim=Dimensions[matr[[1]]], min, ind, tuples, payoffTuples},(*matr\[LeftDoubleBracket]1\[RightDoubleBracket] has the same dimensions as all other m\[LeftDoubleBracket]2\[RightDoubleBracket],...,m\[LeftDoubleBracket]n\[RightDoubleBracket]*)
Table[
min=Table[0,dim[[player]]];
Do[
ind=Table[Range[dim[[j]]],{j,Length[matr]}]; (* list of strategy sets *)
ind[[player]]={str}; (* strategy set of the player is set simply formed by one element: {str} *)
tuples=Tuples[ind]; (* generate the tuples *)
payoffTuples=Table[matr[[player,Sequence@@t]],{t,tuples}]; (* the variable player gives the matrix of the player; other indeces give the payoff value *)
min[[str]]=Min[payoffTuples], (* for every player *)
{str,dim[[player]]}
];
"Player "<>ToString[player] -> <|"Strategy"->maxPositions[min],"Payoff"->min[[maxPositions[min]]][[1]]|>,
{player,Length[matr]}
]
]
It is used to compute MaxMin strategies. This concept is more simple in comparison with the Nash equilibrium. It needs finding for every fixed strategy of the player the worst response of the other players. After knowing all such worst responses, every player computes the best from them, that being the MaxMin strategy.
The following example illustrates how the function is applied really for the same above matrices:
In[3]:= GameTheory[{a, b},
Method -> {"Criteria" -> "Maximize", "Concept" -> "MaxMin",
"Strategy" -> "Pure"}]
Out[3]= {"Player 1" -> <|"Strategy" -> {1, 2}, "Payoff" -> 2|>,
"Player 2" -> <|"Strategy" -> {1}, "Payoff" -> 3|>}
Sure, the function solves the above problems for an arbitrary number of players:
------------------------------------------------------------------ 5 player game ---------------------------------------------------------------
In[4]:= Clear[a, b, c, d, e]
a = RandomInteger[{-10, 1000}, {5, 5, 5, 5, 5}];
b = RandomInteger[{-10, 1000}, {5, 5, 5, 5, 5}];
c = RandomInteger[{-10, 1000}, {5, 5, 5, 5, 5}];
d = RandomInteger[{-10, 1000}, {5, 5, 5, 5, 5}];
e = RandomInteger[{-10, 1000}, {5, 5, 5, 5, 5}];
MatrixForm /@ {a, b, c, d, e};
In[5]:= GameTheory[{a, b, c, d, e},
Method -> {"Criteria" -> "Maximize", "Concept" -> "MaxMin",
"Strategy" -> "Pure"}]
Out[5]= {"Player 1" -> <|"Strategy" -> {5}, "Payoff" -> -7|>,
"Player 2" -> <|"Strategy" -> {1, 5}, "Payoff" -> -7|>,
"Player 3" -> <|"Strategy" -> {2}, "Payoff" -> -7|>,
"Player 4" -> <|"Strategy" -> {4}, "Payoff" -> -8|>,
"Player 5" -> <|"Strategy" -> {3}, "Payoff" -> -8|>}
In[6]:= GameTheory[{a, b, c, d, e},
Method -> {"Criteria" -> "Maximize", "Concept" -> "NashEquilibrium",
"Strategy" -> "Pure"}]
Out[6]= {<|"Player 1" -> 1, "Player 2" -> 1, "Player 3" -> 2, "Player 4" -> 2,
"Player 5" -> 4|> -> {807, 935, 772, 829, 986}, <|"Player 1" -> 3,
"Player 2" -> 1, "Player 3" -> 5, "Player 4" -> 5,
"Player 5" -> 3|> -> {824, 939, 621, 776, 874}}
It is important to remark here that not all pure strategy games have Nash equilibria. But, all mixed-strategy games have Nash equilibria.
Next private function solve the problem of Nash equilibrium set finding in two-matrix mixed-strategy games:
mixedNashEquilibria[m_]:=With[{a=m[[1]],b=m[[2]]},
NESet={};
Do[
\[DoubleStruckCapitalU]=Range[i+1,Dimensions[a][[1]]];
Do[
Do[
If[X[b,i,j,\[DoubleStruckCapitalI],{}]==0,Break,Continue];
\[DoubleStruckCapitalV]=Range[j+1,Dimensions[a][[2]]];
Do[
If[Y[a,i,j,\[DoubleStruckCapitalI],\[DoubleStruckCapitalJ]]!=0&&X[b,i,j,\[DoubleStruckCapitalI],\[DoubleStruckCapitalJ]]!=0,
NESet=AppendTo[NESet,{XOut[b,i,j,\[DoubleStruckCapitalI],\[DoubleStruckCapitalJ]],YOut[a,i,j,\[DoubleStruckCapitalI],\[DoubleStruckCapitalJ]]}],
Break
],
{\[DoubleStruckCapitalJ],Subsets[\[DoubleStruckCapitalV]]}
],
{j,Dimensions[a][[2]]}
],
{\[DoubleStruckCapitalI],Subsets[\[DoubleStruckCapitalU]]}
],
{i,Dimensions[a][[1]]}
];
DeleteDuplicates@NESet
]
The intersection method used for two-matrix mixed strategy games is described in details in [2]. Next, we illustrate its working out in the above form codding:
Clear[a, b]
a = {{2, 2, 3}, {7, 2, 2}, {1, 1, 4}};
b = {{5, 6, 1}, {5, 2, 3}, {3, 5, 7}};
MatrixForm /@ {a, b};
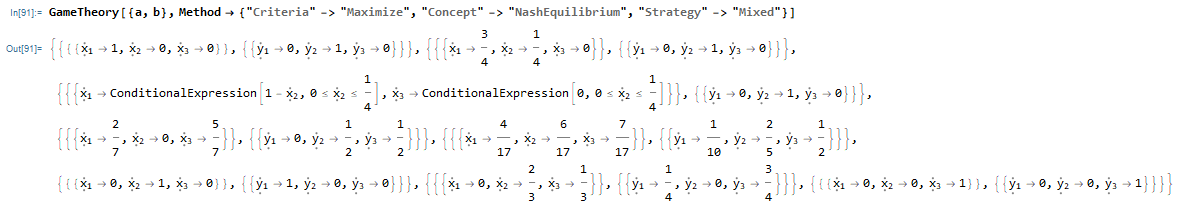
For some strategic games it is possible to present graphically the set of Nash equilibria [6].
All the code is very large, so we present here only on function used to manipulate all graphics objects appearing in the final image:
game2x2Plot[m_]:=Module[{matr=m},
{{{\[DoubleStruckA]11,\[DoubleStruckA]12},{\[DoubleStruckA]21,\[DoubleStruckA]22}},{{\[DoubleStruckB]11,\[DoubleStruckB]12},{\[DoubleStruckB]21,\[DoubleStruckB]22}}}=matr;
Manipulate[
Grid[{{Graphics[{Thick,
Blue,g1[a11-a12-a21+a22,a12-a22],
Green,g2[b11-b12-b21+b22,b21-b22],
Red,PointSize[Large],nes[a11-a12-a21+a22,a12-a22,b11-b12-b21+b22,b21-b22]},
PlotRange->{{0,1},{0,1}},Axes->True,AxesLabel->{"\!\(\*SubscriptBox[\(x\), \(1\)]\)","\!\(\*SubscriptBox[\(y\), \(1\)]\)"},
ImageSize->{300,300}]},{" "},{Text@Style["Reference Nash Equilibria",Bold]},
{Text@Style[nes[a11-a12-a21+a22,a12-a22,b11-b12-b21+b22,b21-b22][[1,1]],Bold]}},ItemSize->{Automatic,{10,1,1,3}},Alignment->{Center,Top}
],
Style["Matrix A",Bold],
{{a11,\[DoubleStruckA]11,"\!\(\*SubscriptBox[\(a\), \(11\)]\)"},-10,10,1,Appearance-> "Labeled",ImageSize->Tiny},
{{a12,\[DoubleStruckA]12,"\!\(\*SubscriptBox[\(a\), \(12\)]\)"},-10,10,1,Appearance-> "Labeled",ImageSize->Tiny},
{{a21,\[DoubleStruckA]21,"\!\(\*SubscriptBox[\(a\), \(21\)]\)"},-10,10,1,Appearance-> "Labeled",ImageSize->Tiny},
{{a22,\[DoubleStruckA]22,"\!\(\*SubscriptBox[\(a\), \(22\)]\)"},-10,10,1,Appearance-> "Labeled",ImageSize->Tiny},
Delimiter,{{NonAntagonistic,True, "NonAntagonistic"},{True,False}},
Delimiter,Style["Matrix B",Bold],
{{b11,\[DoubleStruckB]11,"\!\(\*SubscriptBox[\(b\), \(11\)]\)"},-10,10,1,Enabled->NonAntagonistic,Appearance-> "Labeled",ImageSize->Tiny},
{{b12,\[DoubleStruckB]12,"\!\(\*SubscriptBox[\(b\), \(12\)]\)"},-10,10,1,Enabled->NonAntagonistic,Appearance-> "Labeled",ImageSize->Tiny},
{{b21,\[DoubleStruckB]21,"\!\(\*SubscriptBox[\(b\), \(21\)]\)"},-10,10,1,Enabled->NonAntagonistic,Appearance-> "Labeled",ImageSize->Tiny},
{{b22,\[DoubleStruckB]22,"\!\(\*SubscriptBox[\(b\), \(22\)]\)"},-10,10,1,Enabled->NonAntagonistic,Appearance-> "Labeled",ImageSize->Tiny},
Delimiter,
Style["Matrices A and B",Bold],
Dynamic[
TableForm[
{{ToString[a11]<>" , "<>ToString[If[NonAntagonistic,b11,b11=-a11]],
ToString[a12]<>" , "<>ToString[If[NonAntagonistic,b12,b12=-a12]]},
{ToString[a21]<>" , "<>ToString[If[NonAntagonistic,b21,b21=-a21]],
ToString[a22]<>" , "<>ToString[If[NonAntagonistic,b22,b22=-a22]]}},
TableHeadings->{{"1","2"},{" 1"," 2"}},
TableSpacing->{2,2}
]
],
SaveDefinitions->True
]
]
In practice, the function is used at it follows:
Clear[a, b]
a = {{5, 3}, {7, 2}};
b = {{3, 6}, {5, 3}};
MatrixForm /@ {a, b};
GameTheoryPlot[{a, b}]
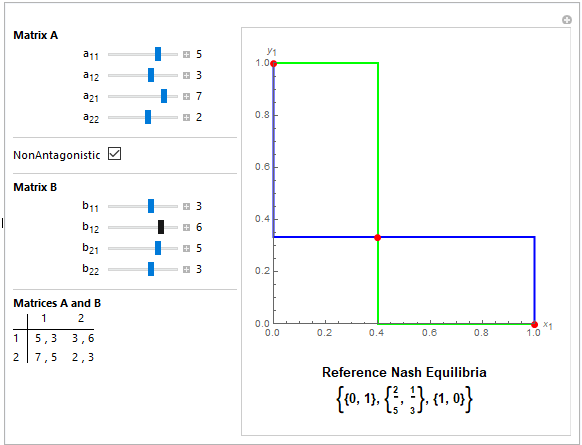
Conclusions
We have passed only a first pre-initial state of the package construction. There is a lot of things that must be done to establish a successful game theory package. We can only emphasised here some other stages. So, we intend to develop the package in several successive stages and directions:
- At the first initiation stage we plan to enlarge the number of strategic form game theory problems solved by the package, and to include more plotting possibilities.
- At the second stage we intend to develop package functionality in order to solve extensive form games, and to include their abundant plotting functionality.
- At the third stage, we are considering adding support for cooperative games.
- At the fourth stage, we plan to consider differential games and control.
- Next stages will include multi-criteria mixtures of simultaneous and sequential games, as well as a lot of applied problems from all the human activity.
Bibliography
- Ungureanu, Valeriu, Nash equilibria set computing in finite extended games, CSJM, 2006, Vol. 14, No. 3 (42), pp. 345-365.
- Ungureanu, Valeriu, "Pareto-Nash-Stackelberg Game and Control Theory", Springer International Publishing, 2018, XXI + 343 pp.
- Ungureanu, Valeriu, Nash equilibrium set function in dyadic mixed-strategy games, CSJM v .25, n .1 (73), 2017.
- Nash J.F., Noncooperative game, Annals of Mathematics, 54, 1951, pp. 280-295.
- Sagaidac, M., and Ungureanu, V., Operational research, Chi\sinau, CEP USM, 2004, 296 p. (in Romanian)
- Ungureanu, V., Nash Equilibrium Sets in Dyadic Bimatrix Mixed-Strategy Games,