Empirically derived conditional distribution of System symbols
Range->Length->Part is commonly found in:
Given that Mathematica is a symbolic language it would be interesting to view the relationships between these symbols e.g. Length[List[1,2,3]] implies a relationship of Length -> List.
Since we do not know this information, we will have to retrieve it. For that, I headed to GitHub. Note: GitHub's public api limits the rate you can query to $1$ query every $30$ seconds (so the crawl takes many hours).
(* Get repositories marked with Mathematica as a language *)
githubResults = SearchRepositories["Mathematica"];
"8586 public repositories with language(s): Mathematica.
Only the first 1000 are available via the public api."
(* Get repository names *)
repositoriesWithMathematica = Normal[githubResults[All, "full_name"]];
(* Search for .nb files in these repos *)
notebookResults = SearchNotebooks[repositoriesWithMathematica];
"3525 notebooks found."
(* Now go download all of those .nbs *)
files = DownloadRawURLs[notebookResults, CreateDirectory[]]
With our $3,525$ notebooks, we are ready to try and extract the Symbol->Symbol relationship (thanks to Carl Woll for helping with this part):
Test for system symbol
SetAttributes[systemSymbol, {Listable, HoldFirst}]
systemSymbol[Symbol[_String]] = False;
systemSymbol[s_Symbol] := Context[s] === "System`"
systemSymbol[_] = False;
Extract symbol relationships
Note, we replace all non system symbols with a placeholder "NonWolfram".
NBExpressionRelations[file_] := Module[
{
nb = NotebookImport[file, "Input"],
expr =
Cases[nb,
p : _Symbol?systemSymbol[s_Symbol, ___] :> Hold[p], {3, Infinity}]
},
Cases[nb,
p_Symbol?systemSymbol[s_Symbol[___], ___] :>
If[Context[s] === "System`", RuleDelayed[p, s],
RuleDelayed[p, "NonWolfram"]], {3, Infinity}]
]
Just loop this over all the files to get the data, and then
(* if you want to keep them by file *)
results = AssociationThread[fileNames, expressionData]
(* or *)
data = Flatten[expressionData]
Explore System symbol relationships
(* Tally over the keys (symbols used as Heaed) *)
tally = Tally[data[[;; , 1]]];
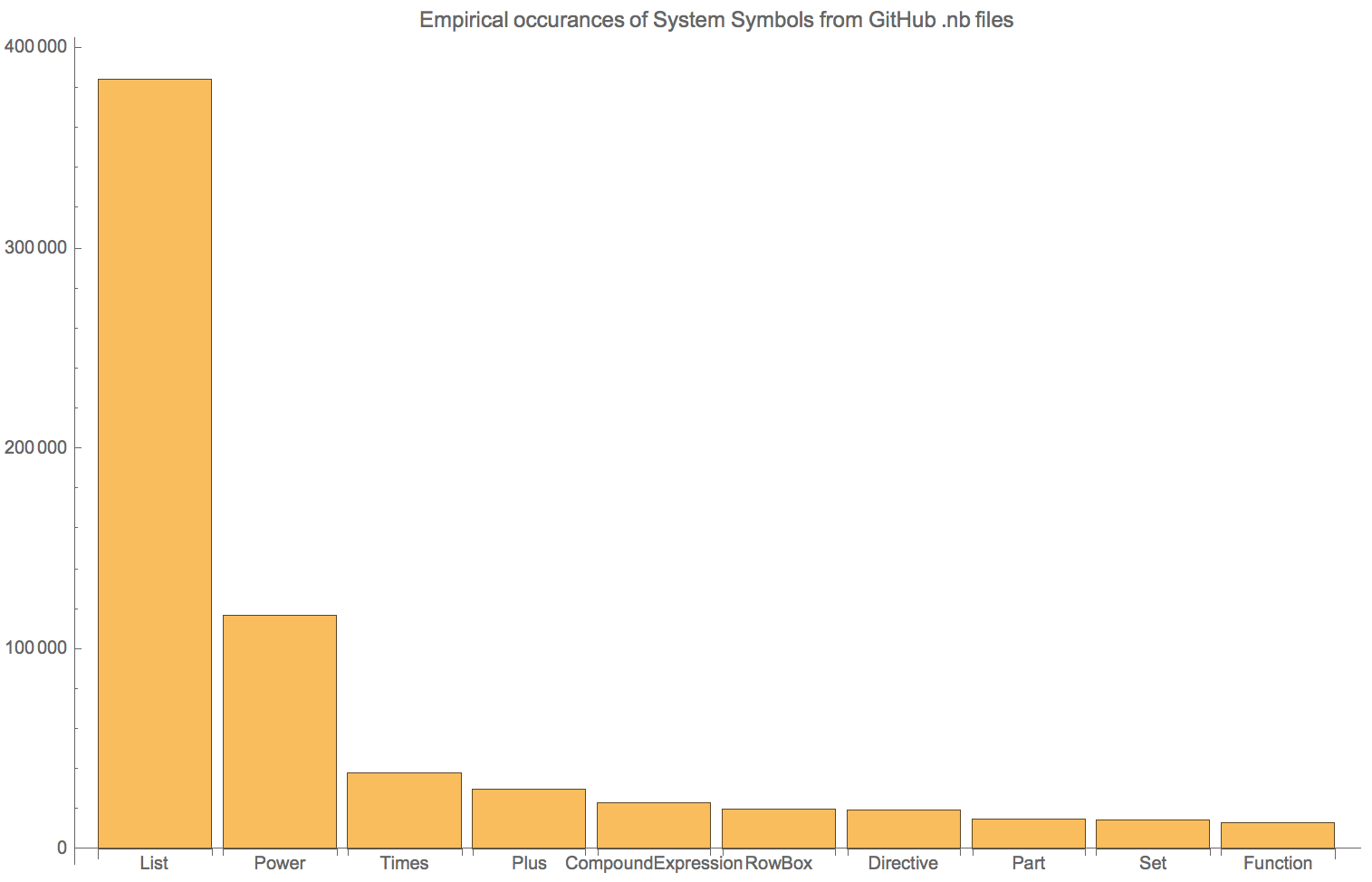
If we just look at the symbols by occurrence, we see that unsurprisingly List is the most prominent:
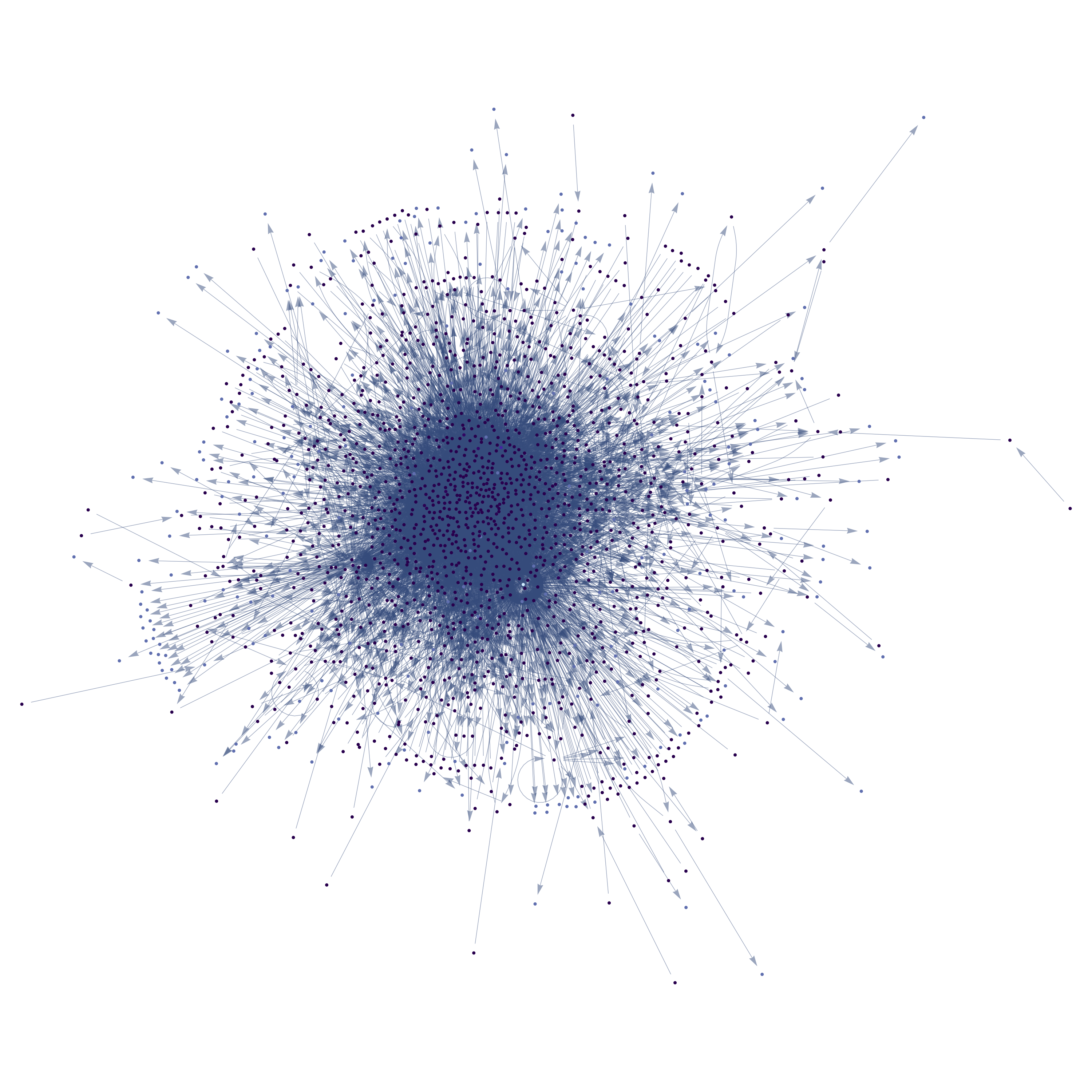
We can view the interaction network as well, where the vertices are colored and sized by occurrence.
ToString[#[[1]]] \[DirectedEdge] ToString[#[[2]]] & /@ data;

The light blue dot near the center is List.
This isn't all that informative, but we can make the frequency distribution of the symbols
NormalizeAssociation[assoc_] :=
With[{tots = Total[assoc]}, Reverse[Sort[Map[N[#/tots] &, assoc]]]]
(* Occurances of symbols *)
symOccur = Association @@ Rule @@@ tally;
(* Probability of symbols *)
symProb = NormalizeAssociation[symOccur];
and then the conditioned distribution
(* Conditional occurances of symbols *)
symCondOccur =
Map[Association @@ Rule @@@ Tally[#[[;; , 2]]] &,
GroupBy[Rule @@@ data, First]];
(* Conditional probability of symbols *)
symCondProb = Map[NormalizeAssociation, symCondOccur];
with this we can traverse our network (in this case we take only the most likely at each step, which may not be the best approach overall)
nextSymbol[symbol_] := Module[
{
dist, max, sel, key
},
If[symbol == Nothing, Return[Nothing]];
dist = symCondProb[symbol];
(* Maybe we never saw this symbol as head in our data *)
If[MissingQ@dist, Return[Nothing]];
max = Max[symCondProb[symbol]];
sel = Select[dist, max == # &];
(* Likewise perhaps selection failed as it was not connected to anything *)
If[sel == <||>, Return[Nothing]];
key = First@Keys[sel];
(* Since we always take max,
if key\[Equal]symbol we will go in circles *)
If[key == symbol, Return[Nothing]];
Return[key];
]
```
Now we can see some promising results:
NestList[nextSymbol[#] &, Range, 5] `` yields:{Range, Length, Part}`
NestList[nextSymbol[#] &, Import, 4]
yields: {Import, StringJoin, NotebookDirectory, EvaluationNotebook}
so it seems people tend to write Range[Length[Part[...]]] e.g. Range@Length@myData[[;;,1]] and Import[StringJoin[NotebookDirectory[],...]]
Whats next?
Next it would be interesting to throw these notebooks into a language model.
Code
Attached is the code for crawling, everything else of relevance is above.
 Attachments:
Attachments: