Introduction
The tropical semi-ring is the set R of real numbers equipped with the operations of tropical addition and tropical multiplication, which corresponds to classical minimum and addition respectively. The min-plus algebra comprises one half of tropical mathematics. The other semi-ring is max-plus algebra where the tropical addition is classical maximum. The goal of my project is to implement and investigate arithmetic and matrix algebra over tropical semi-rings using Wolfram Language and explore some of its applications.
I started by implementing the basic functions to compute linear algebra operations and then extended it for computing the general matrix operations over tropical semi-ring. Let's start with some function definitions for matrices:
Matrix operations
Determinant
TropicalDeterminant[a_List] := With[{n = First[Dimensions[a]]},
Min[Total[Table[Extract[a, Thread[{Range[n], perm}]], {perm, Permutations[Range[n]]}], {2}]]] /; SquareMatrixQ[a] == True
Singularity
TropicalSingularQ[a_List] :=
With[{terms = Table[Extract[a, Thread[{Range[First[Dimensions[a]]], perm}]],
{perm, Permutations[Range[First[Dimensions[a]]]]}]},
If[First[Counts[Sort[Total[terms, {2}]]]] > 1 , True, False]] /; SquareMatrixQ[a] == True
Tropical Rank
TropicalRank[a_List] := ( r = First[Dimensions[a]]; minor = Table[Flatten[Minors[a, i, Identity], 1], {i, r}];
While[AllTrue[minor[[r]], TropicalSingularQ], r--];
r ) /; SquareMatrixQ[a] == True
Adjoint matrix
TropicalAdjointMatrix[a_List] := With[{n = First[Dimensions[a]],
m = Minors[a /. {Infinity -> w}, First[Dimensions[a]] - 1, Identity]},
Transpose[Partition[TropicalDeterminant/@(Flatten[Reverse[Reverse[m,n-1]],1] /.{w -> Infinity}),n]]]/;SquareMatrixQ[a]==True
Pseudo Inverse
TropicalMatrixInverse[a_List] := TropicalAdjointMatrix[a] - TropicalDeterminant[a] /; SquareMatrixQ[a] == True
Tropical polynomials
Variable is a matrix
TropicalPolynomial[p_List, x_List] := ( n = First[Dimensions[x]];
temp = First[p] + TropicalIdentityMatrix[n];
For[i = 0, i < Length[p], i++,
temp = TropicalPlus[TropicalMatrixTimes[(temp), x], (p[[i + 1]] + TropicalIdentityMatrix[n])];];
temp
)
Variable is a number
f[a_, b_] := tropicalPlus[tropicalTimes[a, x], b]
TropicalPolynomial[p_List, x_] :=
Fold[ f, p] /. {tropicalPlus -> Min, tropicalTimes -> Plus}
Polynomial multiplication
TropicalPolynomialTimes[a_, b_, x_] := Expand[a*b] /. {Plus -> Min, Times -> Plus, x^n_ -> n*x}
Applications of tropical algebra
While exploring about tropical algebra, I came across some of its interesting applications in graph theory and cryptography which I implemented using the package I developed. Here are a few examples of them.
Shortest path using Tropical Algebra
Given a directed graph G = {V, E} of n vertices and a transition cost matrix $C\in \mathbb{R}_{\text{nxn}}$ where $C_{\text{ij}}$ the weight of every edge (i, j). In tropical algebra, $C^m{}_{\text{ij}}$ = minimum cost of moving from vertex i to vertex j in at most m steps.
Let's first take a graph with non negative elements.
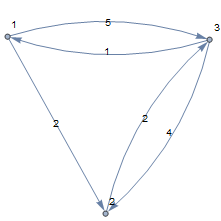 $$ C = \left( \begin{array}{ccc} 0 & 2 & 5 \\ \infty & 0 & 2 \\ 1 & 4 & 0 \\ \end{array} \right) $$
$$ C = \left( \begin{array}{ccc} 0 & 2 & 5 \\ \infty & 0 & 2 \\ 1 & 4 & 0 \\ \end{array} \right) $$
Square of the matrix C will give the shortest path between every pair of vertices in the graph.
TropicalMatrixSquare[c] // MatrixForm
$$ \left( \begin{array}{ccc} 0 & 2 & 4 \\ 3 & 0 & 2 \\ 1 & 3 & 0 \\ \end{array} \right) $$
In the case where not all elements are non-negative, $C^m{}_{\text{ij}}$ is the minimum cost of moving from vertex i to vertex j in at most m steps.
Note: If all the elements in the cost matrix are positive, then $C^m = C^2$ for m >= 2, since any trip of size 3 or more steps contains a circuit.
Key generation for encryption
Let R be the tropical algebra of square matrices of size n over integers. Let A, B R be public matrices such that $A\otimes B \neq B \otimes A$ :
Let's say Alice selected two random polynomials p1 and p2 and Bob selected two random polynomials q1 and q2. Alice sends $p1[A] \otimes p2[B]$ to Bob.
p1[A] = TropicalPolynomial[p1, A];
p2[B] = TropicalPolynomial[p2, B];
p = TropicalMatrixTimes[p1[A], p2[B]];
Bob sends $q1[A] \otimes q2[B]$ to Alice.
q1[A] = TropicalPolynomial[q1, A]
q2[B] = TropicalPolynomial[q2, B];
q = TropicalMatrixTimes[q1[A], q2[B]];
Now Alice computes$ p1[A] \otimes q \otimes p2[B] $ and Bob computes $q1[A] \otimes p \otimes q2[B]$:
keyA = TropicalMatrixTimes[TropicalMatrixTimes[p1A, q], p2B]
keyB = TropicalMatrixTimes[TropicalMatrixTimes[q1A, p], q2B]
Due to the properties of tropical semi-rings, keyA and keyB are equal and hence a secure private key. The range for variables I selected typically produces a key of size 10^30. To break the cryptosystem based on this key, one has to solve a system of tropical polynomials which is proved to be an NP hard problem. Infeasibility of such a computation makes this cryptosystem much more secure and invulnerable to the known linear attacks. Moreover at no point in the key generation process one is performing classical multiplication because only minimum and addition are the two operations used, which means this algorithm is more efficient. A key produced by this algorithm produces a key like:

Future Work
Since tropical algebra itself is a new branch of mathematics, much of its applications are not known to us. Due to the efficiency of matrix multiplication in tropical algebra, some interesting results for graph theory can be derived and possibly a deeper connection between graph theory and tropical algebra can be established. Other than graph theory applications, NP Hardness of solving systems of linear equations can be used as the basis of creating much stronger cryptosystem than already existing. Tropical algebra is an integral part of geometric combinatorics and algebraic geometry. Tropical geometry is a branch of geometry manipulating with certain piecewise-linear objects that take over the role of classical algebraic varieties. Tropical algebra can hence be used to understand the discrete event dynamic system (DEDS). With the package developed for the tropical algebra, implementation for such systems will become much easier.
The tropical algebra package can be installed via https://github.com/RajAnjali/Summer2018Starter-master/blob/master/Summer2018Starter-master/StudentDeliverables/Tropical%20Algebra.m