Introduction
My project for Wolfram Summer School is creating a network that can lean the pattern of the input image data and generate new images that follow the same pattern. The model is based on this paper [1], where the authors illustrated the idea of Variational Autoencoders. The value of Image data is represented as a multi-dimensional probability distribution. Each pixel value on the image is a point sampled from a probability distribution. For instance, a greyscale image of 28*28 resolution is a 784-dimension probability distribution. Variational Autoencoders maps the images high dimensional space into a lower dimension space, and can also recover the image data back to the high dimension from that lower dimension space. The model consists of three parts: the encoder layer, reparametrize layer and the decoder layer. Here is an image of how it works.
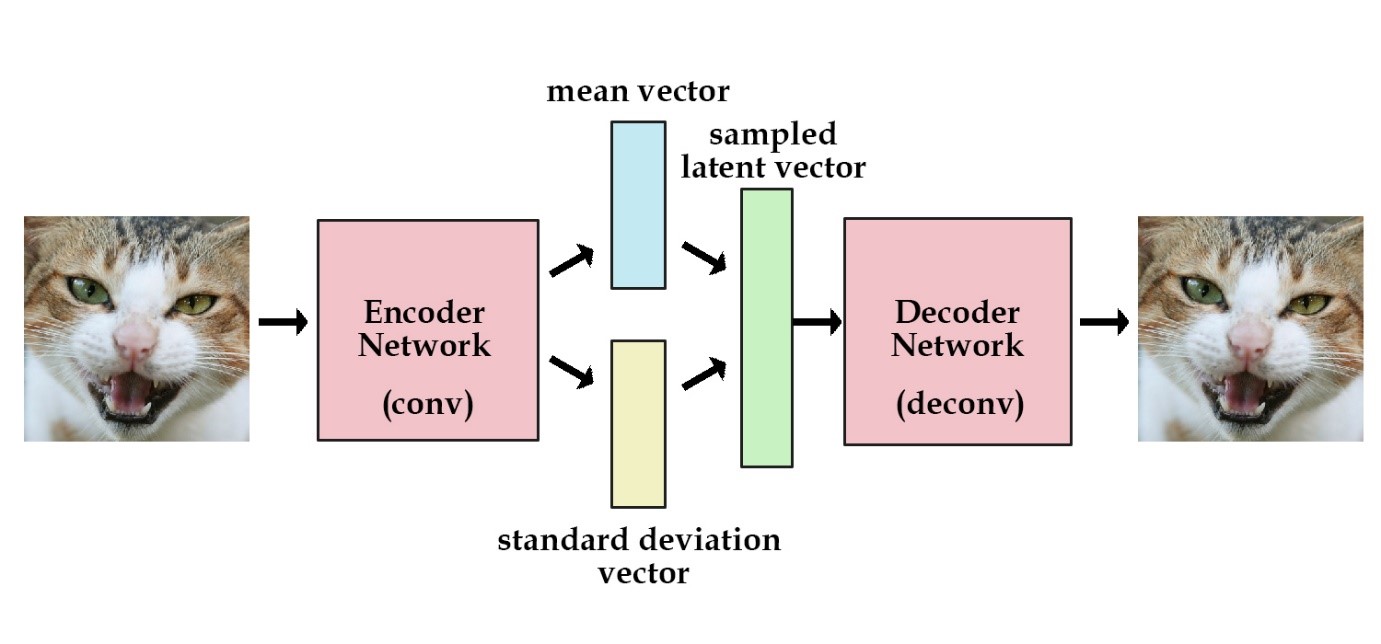
In other words, the network is trying to do two things:
- Find the distribution of latent vector (z), given the input image. q(z|x)
- Recover the distribution of the image, given the latent vector (z). p(z|x)
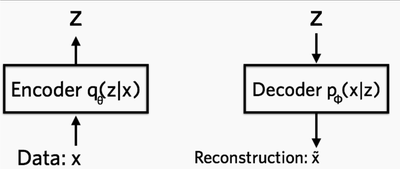
Network Implementation
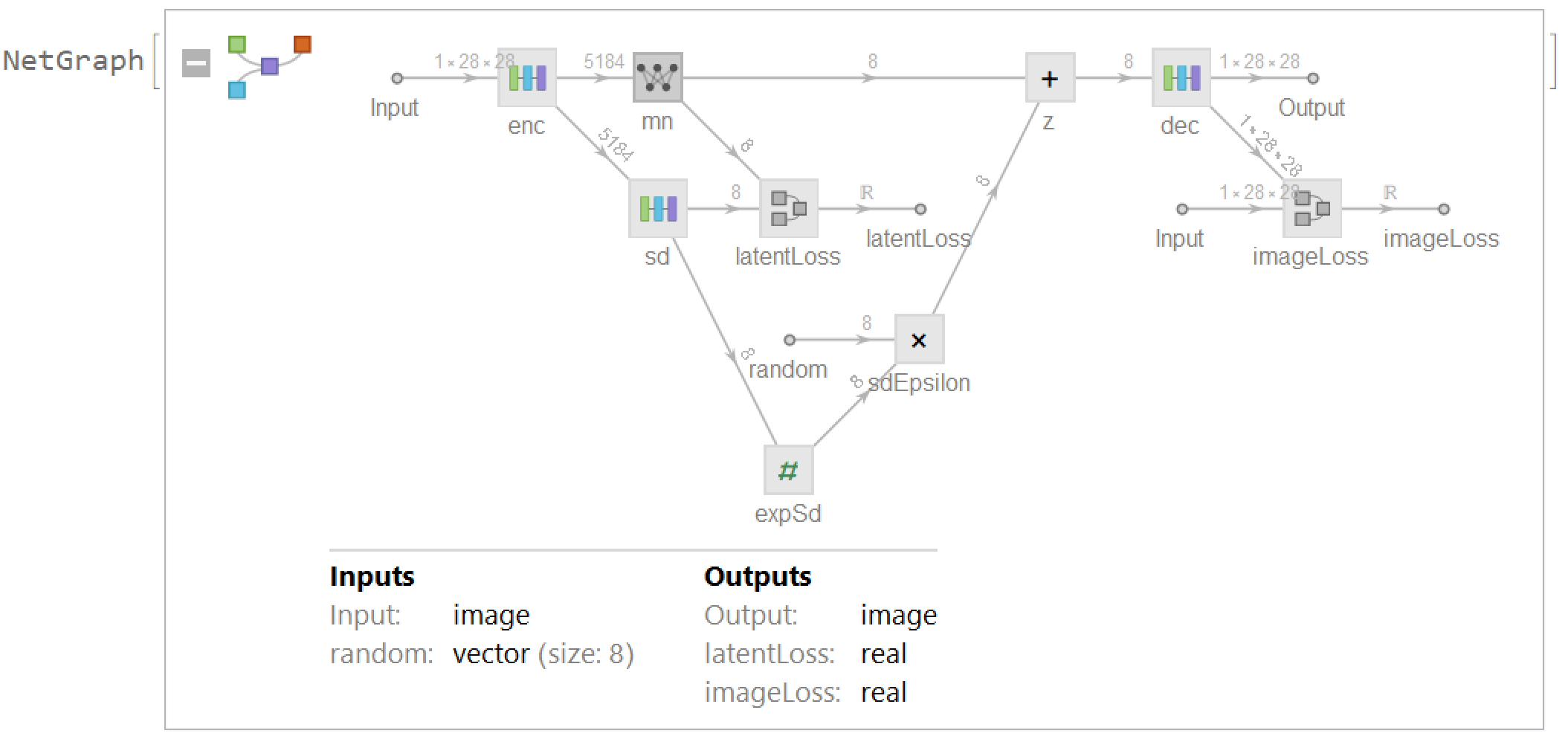
Variational Autoencoders consists of 3 parts: encoder, reparametrize layer and decoder. Encoder is used to compress the input image data into the latent space. Decoder is used to recover the image data from the latent space. Reparametrize layer is used to map the latent vector spaces distribution to the standard normal distribution. We trained the network on the MNIST handwritten digits dataset using a latent vector of size 8.
Encoder Layer
Encoder Layer Encoder layer consists of 3 convolution layer extract the data from the input image data, then flatten it at the end with an output size of 5184. The output will be connected to the reparametrize layer to map to the latent vector space.
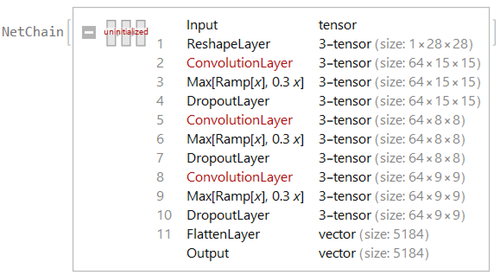
Decoder Layer
Decoder layer takes a vector of length 8 from the latent vector space, then recreates the image using deconvolution layer. The net model is as followed:
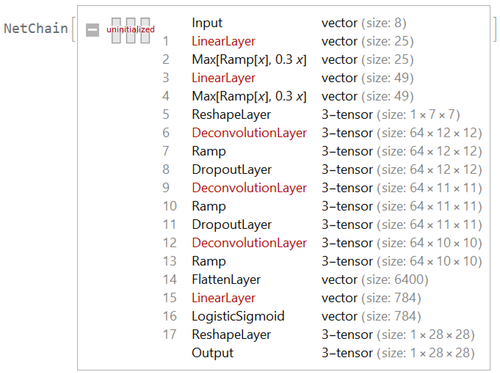
Reparametrize Layer
In the reparametrize layer, we try to find the mean vector and standard deviation vector for each sample input to the encoder layer. We therefore use dense layer to find them from the output of the encoder layer so that we can map this output to the standard normal distribution.
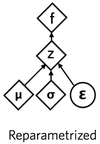
Here is the Network.
mn = LinearLayer[nlatent]
sd= NetChain[{LinearLayer[nlatent],ElementwiseLayer[#*0.5&]}]
expSd = ElementwiseLayer[Exp[#]&]
z =TotalLayer[];
Loss Layer
We use two loss functions. One is the mean squared loss layer, which is used to measure the difference between the reconstructed images and the input images. Notice the output is times by 12828 as we want the total loss of two images
Another lost function is KL-Divergence which is a measure of how similar wo distributions are, so that we can map the distribution of latent vector space to normal distribution. The formula for KL-Divergence is:
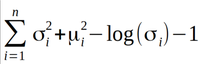
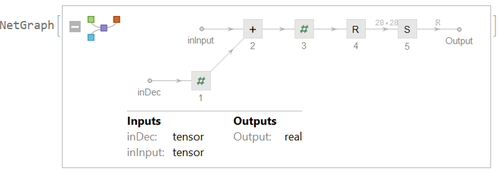
Here is the network implementation:
latentLoss = NetGraph[
{ElementwiseLayer[-0.5*# &], TotalLayer[],
ElementwiseLayer[-(#^2) &], ElementwiseLayer[-Exp[2*#] &],
ElementwiseLayer[1 + 2*# &], SummationLayer[]},
{
NetPort["mn"] -> 3,
NetPort["sd"] -> 4,
NetPort["sd"] -> 5,
{3, 4, 5} -> 2 -> 6 -> 1
}
]
Full network model:
Generating image
In order to sample images using Variational Autoencoders model, we extract the decoder part of the model. To generate new images, we feed decoder with vectors of length 8 that are sampled from the standard normal distribution.
Result
We have successfully trained a model that produce recognisable MNIST handwritten digits.

Results from training on 1072 Monet's paintings:

Conclusion
The network was trained on MNIST datasets which consists of 60000 images. The model was trained for 2000 iterations using a batch size of 32, with ADAM Method and a learning rate of 0.0005. The training takes 10 hours to finish. The result we obtained are showed in the section above and are quite good.
Open Problems
The Variational Autoencoders model is efficient only for generating small images. As indicated in [[2]], for synthesizing images of resolution $k^2$, we need $O(k^2)$ number of parameters and the computational complexity is $O(k^2)$. The VAE model could be useful for generating small-scale images such as handwritten digits. But for higher resolution, it tends to produce blur images and network trains inefficiently.
Future Developments
The encoder and reparametrized layer of the Variational Autoencoders can also be combined to predict the probability of the input image, given the distribution of the training data. This can be used for application such anomaly detection. Moreover, to generate higher resolution images, we can try to combine the Variational Autoencoder model (VAE) and Generative Adversarial Network model (GAN). This type of model is called CVAE-GAN, studied in [[3]]. It combines the capability of VAE, which often produces images that follow the input data distribution yet blur, and the advantage of GAN, which produces sharp images yet deviate from the input data distribution.
References
[1] Doersch, C. (2016). Tutorial on variational autoencoders. arXiv preprint arXiv:1606.05908.
[2] Simonovsky, M., & Komodakis, N. (2018). GraphVAE: Towards Generation of Small Graphs Using Variational Autoencoders. arXiv preprint arXiv:1802.03480.
[3] Bao, J., Chen, D., Wen, F., Li, H., & Hua, G. (2017). CVAE-GAN: fine-grained image generation through asymmetric training. CoRR, abs/1703.10155, 5.