A Discourse Language for Card Games
This project aims at constructing a platform to define any card game for Mathematica and further process, play and analyze the game.
We have implemented a simple structure to introduce game state, perform actions on the game state based on defined rules, play and visualize the game automatically, and construct the game tree of possible moves.
The full code notebook, including examples can be found here!
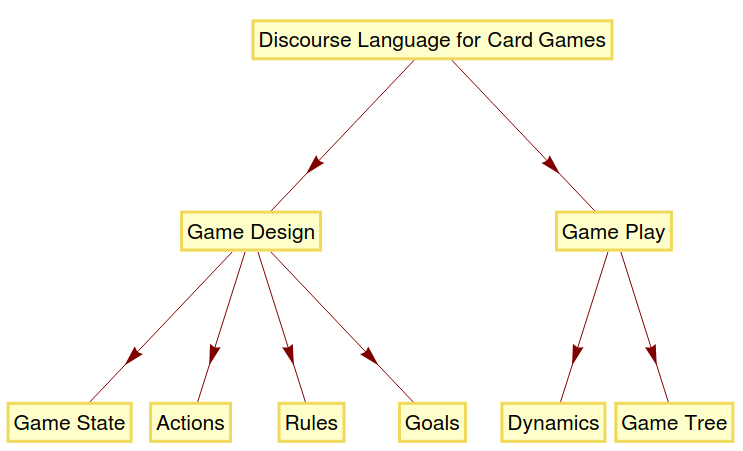
Game Design
In our data structure, there are four main parts of game design: game state, action, rule, and goal
Game State
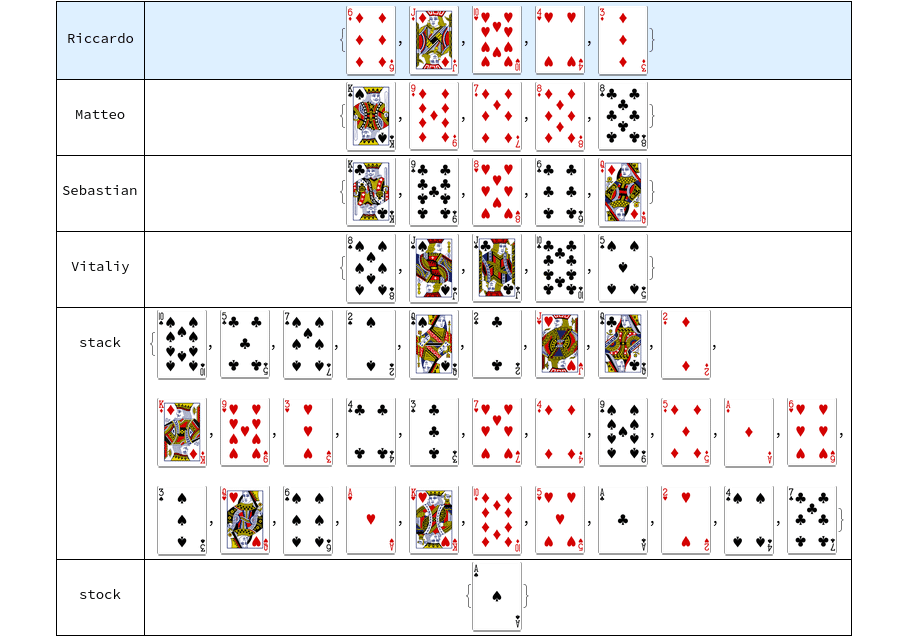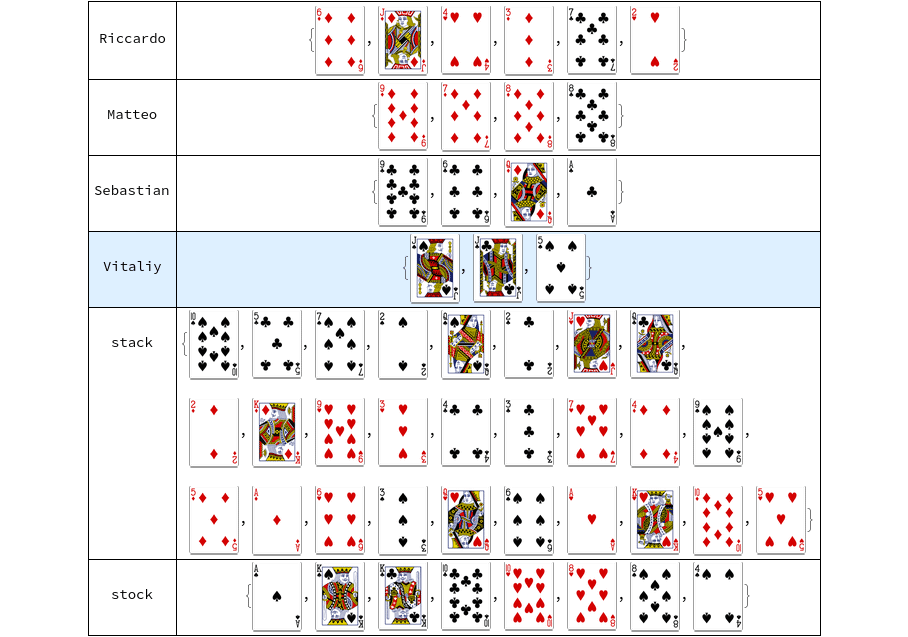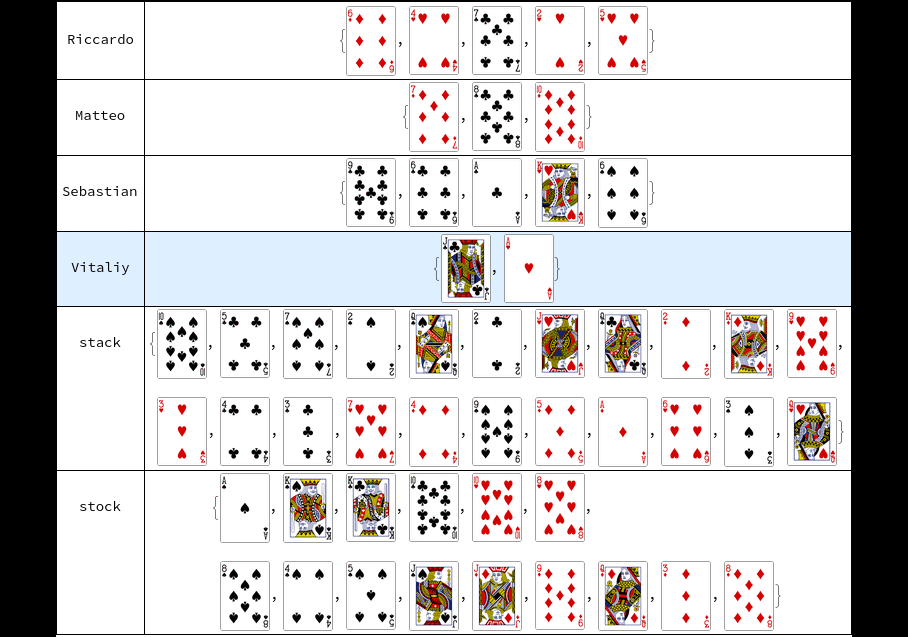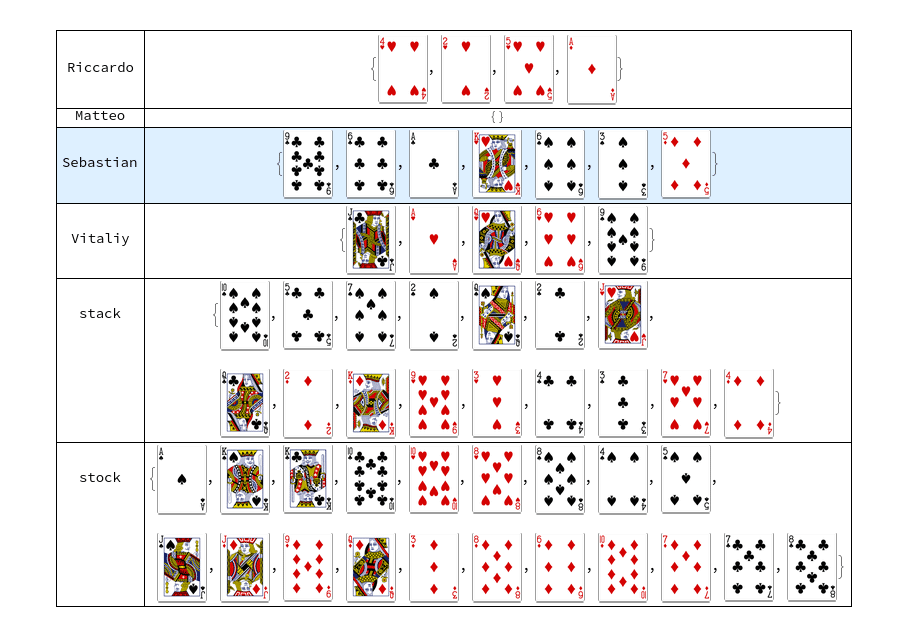
Game state is an association with all needed information in one step of the game. It consists of players and other hands related to a list of cards, and also a control state, showing who controls the game at that step. A game state can be made using implemented functions and can be designed to a specific game:
playersList = {"Riccardo", "Matteo", "Sebastian", "Vitaliy"};
handsN = 5;
initialState = CreateGameState[playersList, handsN];
initialState // VisualizeCardGame

Actions
Actions are functions that map a game state to another one. A simple implemented action is CardMove:
CardMove[hand1_->hand2_, card_][gameState_] := gameState//CardTake[hand1, card]//CardDrop[hand2];
Rules
Rules have a "rule delayed" structure (LHS /; conditions :> RHS), in which the LHS is an association pattern, conditions are the game rules, and RHS is an action. As an example, imagine a this rule: The player in control of the game drops one of his card to stock in case the card has the same suit or same number as the card on top of the stack. This rule can be implemented as follows:
rule1 = gameState:<|___,player_->{___,card1_,___},___,"stock"->{___,card2_},___|> /; (PlayerTurnQ[player][gameState] && SameSuitOrNumberQ[card1,card2]) :> (gameState//CardMove[player->"stock", card1]//NextPlayer);
This structure can easily reproduce next step using Replace function. A list of all possible moves in a game with three rules can be reproduced by:
rules = {rule1, rule2, rule3}
possibleMovesList = ReplaceList[gameState, rules]
Goals
Goal part computes the score and checks the end of the game. The function EndGameQ gets a game state as input and outputs True if it is end of the game state. For instance, if the game ends when a player runs out of cards, this function can be coded as:
EndGameQ[gameState_]:= AnyTrue[gameState/@playersList, (#=={})&];
Furthermore, scores and winners can be defined as a function on gamestate or they might be updated during the game.
Game Play
Dynamics
After the game is designed, it can be played by Mathematica. In a random play, the next game state is selected with equal probability from all possible allowed game state. Then a list of game states is created, representing the game play. The function "PlayRandomList" creates this list till the game ends or to a maximum steps, whichever comes first!
playList = PlayRandomList[initialState, rules, maxsteps];
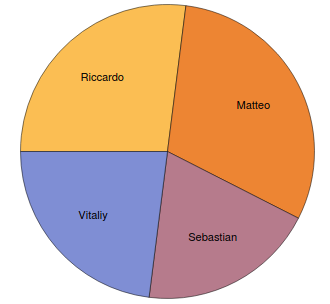
Using this function, statistical analysis on a random play can be generated, such as the probability of wining the game for players. Here is an example of game similar to Crazy Eights. In this game each player at his turn should drop a card on stock with the same suit or same number as stock top. Otherwise, the player draws a card from stack and the game goes to the next player. The goal is to finish cards as soon as possible.
initialStateList = Table[CreateGameState[playersList, handsN], 200];
WinnersList = WinnerofRandomPlay[#, rules] & /@ initialStateList;
PieChart[AssociationMap[Count[WinnersList, #] &, playersList], ChartLabels -> Automatic]
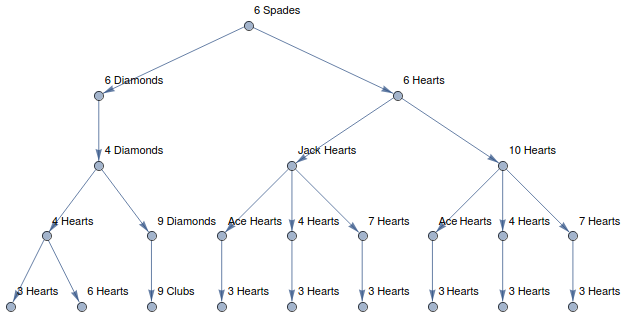
Game Tree
Finally, a game tree of all possible moves from an initial state can be generated. "GameTree" function creates a directed graph of certain depth, using initial state, rules, and depth of the graph. In this graph each vertex is a game state and they are connected in case they are reachable by game rules. PlotGameTree can be designed to plot the graph with vertex labeling of needed information. Here, it labels the vertices with last card in the stock in a tree of the game described above, with depth 4.
graph = GameTree[initialState, rules, 4];
PlotGameTree[graph]
Future Directions
There are several other functions that can be implemented in the game. One of them is a function that outputs the information that each player has at any game state. With this add-on, and also designing a reward or score function, the game can be trained to a neural net and a professional computer game player can be developed. Also, a more general game implementation can be followed using the same method.