Computational Methods for Analyzing Diophantine Equations

The goal of this project was to investigate the solvability of specific cases of Diophantine equations through several forms. In general, it is quite difficult to find generalizable methods for Diophantine equations. As a result, the vast majority of methods used are only useful with regards to strict, specific cases of equations. I wanted to see if, through Mathematica, I could study these methods and discover some sort of pattern which might only arise through empirical investigation.

Definitions of Functions

These functions are used in conjunction to ultimately produce the simple function $Grid[eqnFindSolutions[#, vars] & /@ setofEqns]$ which takes a set of variables and a set of equations and returns a nicely formatted table of the results of the attempts to find solutions. One of three outputs is possible for every equation: either a smallest solution is returned, or No Solution is returned, or Unknown is returned.

$eqnVars[eqn]$ lists the variables in the equation $eqn$.

eqnVars[eqn_]:=Variables[Subtract @@ eqn];

$varsPositive[{x,y,z}]$ outputs $x>0 && y>0 && z>0$. This condition restricts the variables to positive values.

varsPositive[vars_]:=And @@ Map[#>0&,vars];

$eqnResolve[eqn,vars,cond]$ attempts to determine whether the Diophantine equation $eqn$ with variables $vars$ has any positive solutions that satisfy the condition $cond$.

eqnResolve[eqn_,vars_,cond_:True] :=
 Resolve[Exists[vars, eqn && varsPositive[vars] && cond], Integers];

$eqnFindInstance[eqn,vars,cond]$ attempts to find one positive solution to the Diophantine equation $eqn$ with variables $vars$ that satisfies the condition $cond$.

eqnFindInstance[eqn_,vars_,cond_:True] :=
 vars/.Flatten[FindInstance[eqn && varsPositive[vars] && cond,vars, Integers]];

$solSmallerCondition[\{1,2,3\},\{x,y,z\}]$ outputs $(x<1|y<2||z<3)&&(x<=1&&y<=2&&z<=3)$. This condition defines a solution smaller than {1,2,3}.

solSmallerCondition[sol_,vars_]:=
 Or@@MapThread[#1<#2&,{vars,sol}] && And@@MapThread[#1<=#2&,{vars,sol}];

Assuming that a solution exists, $eqnFindSmallestSolution[eqn,vars,cond]$ attempts to find the smallest positive solution to the Diophantine equation $eqn$ with variables $vars$ that satisfies the condition $cond$.

eqnFindSmallestSolution[eqn_,vars_,cond_:True]:=
 NestWhile[
  eqnFindInstance[eqn,vars,solSmallerCondition[#,vars]&&cond]&,
  eqnFindInstance[eqn,vars,cond],
  eqnResolve[eqn,vars,solSmallerCondition[#,vars]&&cond]&
 ];

Given a Diophantine equation $eqn$ with variables $vars$, $eqnFindSolutions[eqn,vars,f]$ attempts to find a smallest positive solution, if one exists. If it can be shown that no solutions exist, then the string No Solution is output. Otherwise, if it cannot be determined whether $eqn$ has a positive solution, then $f[eqn,vars]$ is output. And if the argument $f$ is omitted, then $f$ is assumed to be the constant function that outputs the string Unknown.

eqnFindSolutions[eqn_, vars_, f_:("Unknown"&)] := 
 Switch[
  eqnResolve[eqn, vars], 
  True, 
  {eqn, Flatten[eqnFindSmallestSolution[eqn, vars]]},
  False,
  {eqn, "No Solution"},
  _,
  {eqn, f[eqn,vars]}
 ]

Finding the Smallest Solutions to Diophantine Equations

Case 1. Let's look at the case of $$2x + 3y = n, \ \text{for} \ \ n \in {1, ... ,15 }$$ Start with defining some variables.

vars={x,y};
setofEqns= 2 x + 3 y == # &  /@ Range[1,15];

Now, run eqnFindSolutions.

Grid[eqnFindSolutions[#, vars] & /@ setofEqns]

Case 2. Now, let's look at a more challenging example.

Consider Mordell's equation for specific cases of $n$: $$x^{2} = y^{3} + n , \ \text{for} \ \ n \in {-20, ... ,20 }$$

Again, we will define our variables:

vars = {x,y};
setofEqns= x^2==y^3+ # &  /@ Range[-20,20];

This time, Mathematica's built-in functions don't find all the solutions. Instead, we must use an external resource and the special-case functionality of of our own functions. Listed below are specific values of $n$ which according to the Online Encyclopedia of Integer Solutions here, here and here do not have any solutions.

MordellNoSol = {-3, -5, -6, -9, -10, -12, -14, -16, -17, 6, 7, 11, 13, 14, 20};
MordellNonPos = {4, 5, 10, 16};

In addition, according to this page, when $n=-8$ there is exactly one solution. Evidently, this is the solution $\{x,y\} = \{0,2\}$, which is non-positive. The next function definition provides us with a way to handle these special cases through our standard function.

eqnMordellTest[eqn_, {x,y}]:=
 If[MemberQ[x^2==y^3+ # &  /@ Join[MordellNoSol, MordellNonPos, {-8}], eqn],"No Solution","Unknown"];

Now, to obtain our answers:

Grid[eqnFindSolutions[#, vars, eqnMordellTest] & /@ setofEqns]

And the output will continue further down. Without the special function, the No Solution outputs would be instead Unknowns, since Mathematica's built-in functions can't recognize these cases.

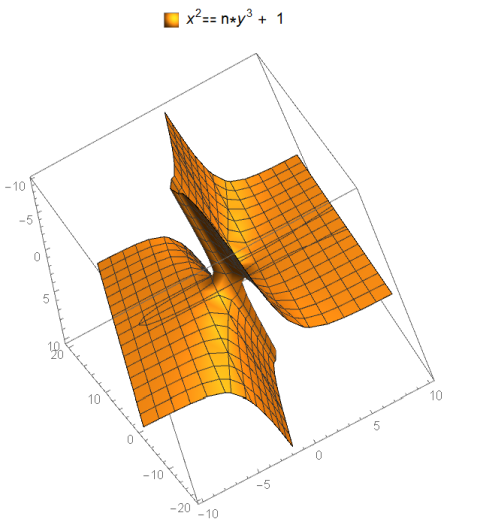
Here is a visualization of Mordell Equations: (Note that a single equation exists for a particular choice of $n$. The plot below graphs many values of $n$ simultaneously to permit the viewer to intuitively understand the range of forms Mordell equations take.)

ContourPlot3D[ x^2==y^3+ n ,{x,-10,10},{y,-10,10}, {n,-20,20}, PlotLegends->Placed[{"x^2==y^3+ n"},Above]]

A Large-Scale Empirical Investigation

An additional section of my project is available to read about on my github. I searched through 1.02 million cases of Diophantine equations to see what patterns would arise.

Future

Empirical investigation has the potential to expose insights about the broad and far-reaching structures underlying the set of these equations. Future work can expand the empirical search in the space of all Diophantine equations and identify threads of decidability which may arise. If anyone else is interested in this topic, message me!