Introduction
Do you remember the experience when you were first introduced to the Nintendo game "Super Mario"? How did you learn to play that game? You were only given 4 keys representing 4 directions to go. You tried them out. You walk, you jump, you get killed by mushrooms, turtles, plants, you fall down the cliff. You restarted again and again. But soon you find that you can kill them by jumping on them, you learned that Mario grows up by eating mushrooms, you even found out ways to skip levels because you accidentally press the down button on a pipe. You gain experience about what gives you a higher reward.
Humans learn from mistakes. By repetitively trying we find out what brings us the highest reward. This is brings the inspiration to the idea of Reinforcement learning for AI. In reinforcement learning, we don't teach the agent what is the correct thing to do, instead we let the agent take in information from the environment, explore the action space, and return the reward for each action it took. The agent will be encouraged to take actions with higher reward. This is the basic idea of reinforcement learning.
There are many types of Reinforcement learning. The one I used is Policy Gradient. The main work that I have done is implementing simple Policy Gradient method into Wolfram Language. On top of that, I tried to implement Advantage Actor Critic (A2C) style Policy Gradient in the hope of speeding up the training process. I used both method to train neural network to play "CartPole", one of the classic problems of Reinforcement learning, which is available in OpenAI Gym, in Wolfram Mathematica and get a average survival time of over 195, where problem is considered to be solved. I wrote a package that can easily be used on any OpenAI Gym environment, which contains both Simple Policy Gradient and A2C method of training in Mathematica.
Theory
Policy Gradient
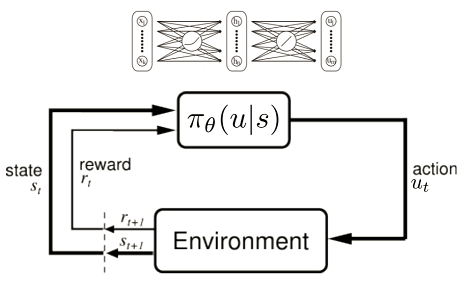
In Policy Gradient, The input to the network is the "observation" from the environment, the output of the network is "action" that the agent is going to take next. After one game (Episode) is over, a discounted reward
$R_t=\sum_{k=0}^\ r_{t+k} \gamma^k$.
$\gamma$ is the discount factor. Discounted reward basically means how much future reward you can get in total if you take a certain step at a certain time. In simple policy gradient method, we also call this discounted reward a "advantage" denoted with $A_i$
We then define a loss function
$L = -\sum_i A_i \log{(P(x_i\|y_i))}$
When we say "the network returns an action", what we are saying is that the network choose an action from a probability distribution of actions. What network actually returns is a list of probability (which is also called a probability vector) of taking different actions. $P(x_i \|y_i) $ denotes the probability in the probability vector that correspond to the action actually taken, which is of course a number smaller than 1. The further $P(x_i \|y_i) $ is to 1, the bigger $ -\log{(P(x_i\|y_i)} $ is. Thus for an action that gets a high reward $A_i$, the further away $P(x_i \|y_i) $ is to 1, the less likely the system will take that action, and the larger the loss will be.
From this point of view, it's not difficult to under stand what this loss function does: when the agent missed the choice of high reward, this loss function is higher, so the agent gets penalized. Since the goal of training a network is to minimize the loss function, this encourages the agent to take actions that grants them higher rewards.
Advantage Actor Critic
Continue the thought from Policy Gradient, let's say you have a observation $S_i$, under this situation, if we choose an action randomly, our average reward $ V^*_i$. But we are taking action according to what our network tells me to, so our actual advantage should be $A_i = R_i - V^*_i$, instead of just $A_i = R_i$. Because we are comparing our result with a baseline to see how much better it is than our baseline.
From this point, let's consider, if we have an estimate of how good our situation is, and we want to find out which step can make the situation better, we need two networks, one is to estimate what is the expected total reward of the current situation, the other finds out which action to take that should lead us a better situation (i.e. leads to a reward that is better than expected reward). This is the basic idea of Advantage Actor Critic method.
Advantage Actor Critic, or A2C, contains two parts, actor and critic. Most commonly, these two parts are included in two different networks. One is the actor network, which gives the optimized action, the other is the critic network, which evaluates the expected reward from current situation. The good thing about A2C is that it makes the network to converge much faster.
Implementation of RL into Wolfram Language
To run the following code and any code from the RLPackage.wl in my github, you need new Neural Network package that is available on Github page linked at the beginning of the article.
Policy Gradient
The cleanest way of implementing Policy Gradient into Mathematica neural network is use LossFunction. We are using a NetChain of Linear Layer and Tanh Elementwise Layer as our policy network. for cartpole, it intakes a vector of 4, which denotes the observation to the environment, and gives a output of an action chosen from 0 (left) and 1 (right)
PolicyNet[]:=
Module[{},
NetInitialize@NetChain[{
LinearLayer[64], Tanh,
LinearLayer[64], Tanh,
LinearLayer[], SoftmaxLayer[]},
"Output"->NetDecoder[{"Class", {0, 1}}], "Input"-> 4]
]
We use following loss function, as I wrote in the "Theory" part.
PolicyLoss[]:=
Module[{},
NetGraph[{
CrossEntropyLossLayer["Index"], ThreadingLayer[#1*#2&]},
{NetPort["Advantage"]->2, 1->2}, "Target"-> NetEncoder[{"Class", {0, 1}}]]
]
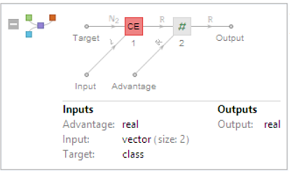
When training the network, we use following:
NetTrain[Policynet[],
GeneratorFunction[*],
LossFunction -> PolicyLoss[], BatchSize -> 32, MaxTrainingRounds -> *]
This allows us to use loss function that we constructed on our own.
A2C
The A2C case is slightly more complicated, because we need to train two nets at the same time. Thus we have to use NetGraph to help us combine the two networks.
The actor network, is actually policy network and will be identical to the previous part. but we have to combine the actual network and the loss together:
FullPolicy[policynet_, policyloss_]:=
Module[{},
NetGraph[
<|"policynet"->policynet, "policyloss"->policyloss|>, {
NetPort["Advantage"]-> NetPort["policyloss", "Advantage"],
NetPort["policyOutput"]-> NetPort["policyloss", "Target"],
"policynet"-> NetPort["policyloss", "Input"]}]
The other net is the critics net, or we can call it a "value net", the loss we use here is mean square loss, again, we have to combine the actual value net and the loss together:
ValueNet[] :=
Module[{},
NetInitialize@NetChain[{
LinearLayer[64], Tanh,
LinearLayer[64], Tanh,
LinearLayer[]},
"Output" ->"Scalar", "Input"-> 4]
]
ValueLoss[]:=
Module[{},
NetGraph[<|"valueloss" -> MeanSquaredLossLayer[]|>, {
NetPort["valueOutput"]->"valueloss" -> NetPort["ValueLoss"]}]
]
FullValue[valuenet_, valueloss_]:=
Module[{},
NetGraph[<|"valuenet"->valuenet, "valueloss"->valueloss|>, {
{"valuenet", NetPort["valueOutput"]}->"valueloss"-> NetPort["ValueLoss"]}]
]
Finally we have to combine the action and critic net together
FullNet[Model_,
policynet_:FullPolicy[PolicyNet[], PolicyLoss[]],
valuenet_:FullValue[ValueNet[], ValueLoss[]]] :=
Module[{fullnet},
If[Model == "PG",
fullnet = PolicyNet[]];
If[Model == "A2C",
fullnet = NetInitialize@NetGraph[{
valuenet, policynet}, {
NetPort["Advantage"]-> 2, 1-> NetPort["ValueLoss"], 2-> NetPort["PolicyLoss"]}]];
fullnet
]
Let's have a look at what our network looks like
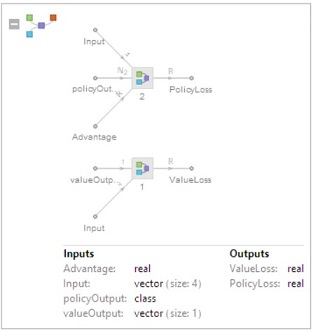
Note that we have multiple loss output in this net, so we need to use LossFunction-> {"lossname"->Scaled[weight]} to help us control the final total loss.
traineda2c =
NetTrain[FullNet[]
GeneratorFunction[*],
LossFunction -> {"PolicyLoss", "ValueLoss" -> Scaled[0.3]},
BatchSize -> 32, MaxTrainingRounds -> *]
Generator Function and data manipulation
The key thing about reinforcement learning is that it generates data using the network that it's training at the same time. We realize this by writing a generator function, which allows us to generate new data periodically every certain amount of batches.
GeneratorFunction[env_, model_, dataperiod_,maxstep_,numEpisode_, gamma_, ports_]:=
Module[{dataoutput, rawdata, roundnumber, policynet, valuenet},
Clear[dataoutput];
If[
Mod[#AbsoluteBatch,dataperiod]==0,
roundnumber = Floor[#AbsoluteBatch/dataperiod];
Clear[rawdata, prepro];
If[model == "PG",
policynet = #Net;
valuenet = 0];
If[model == "A2C",
(*In A2C case, we need to extract the actual actor net and critic net from the full net to use it for prediction*)
policynet =
NetReplacePart[
NetExtract[
NetExtract[#Net,2],1],
"Output"-> NetDecoder[{"Class",{0,1}}]];
valuenet =
NetReplacePart[
NetExtract[
NetExtract[#Net,1],1],
"Output"->NetDecoder["Scalar"]];
];
rawdata = Gameplay[env, policynet, roundnumber, maxstep,numEpisode];
prepro = Prepro[rawdata, gamma, model, valuenet];
];
dataoutput = DataGenerator[prepro,ports,#BatchSize];
dataoutput
]&
When we are using NetTrain in the form of:
NetTrain[net, GeneratorFunction[*]]
it is essentially a loop. For each recursion, NetTrain function takes in a batch of data that generates by GeneratorFunction, use that batch of data to train the net, and then update the net. This updated net will be assigned as an attribute of GeneratorFunction so that it can be called and extracted.
The GeneratorFunction generates data and feed it into NetTrain Function batch by batch, instead of just throw in a complete dataset. Function NetTrain has gives GeneratorFunction three attributes: #BatchSize, #AbsoluteBatch and #Net. #BatchSize denotes the length of data that NetTrain intakes every time as one batch, #AbsoluteBatch denotes the number of batches of data that NetTrain already took in. #Net denotes the neural net that is currently being trained in the NetTrain function.
GeneratorFunction generates new data every dataperiod batches of data. Gameplay function uses the current policy net to play the game and return a list of data in the form of
data = {{observations},{actions},{rewards}}
Prepro function takes in the data generated from Gameplay and calculate discounted reward and advantage,
preprodata = {{observations}, {actions}, {discounted rewards}, {advantage}}
DataGenerator function randomly choose data from preprodata and turn it into the form of association so it can be directly fed into NetTrain function.
feeddata = `<|"Observation"-> {...}, "Action" -> {...}, "Rewards" ->{...}, "Advantage" ->{...}, ...|>`
Performance on CartPole
Use Simple Policy Gradient to train CartPole. Normally the time it takes to get a reward of around 150 is 2000 batches, depending on how well the network is initialized. As is shown in following performance curve diagram, one can see that the performance increase steadily. Considering the uplimit of reward is set to be 200 in actual training so the performance is actually quite good. From second graph, one can see that after 3000 batches of training, most network gets a reward of higher than 180. In practice, one can get a network that can get an average reward of above 190 fairly easily.
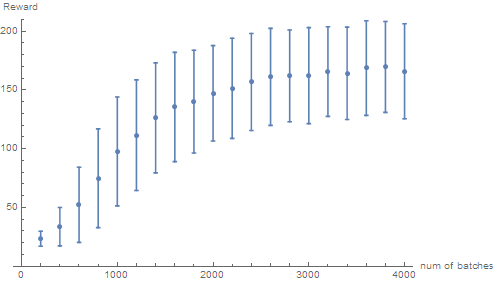
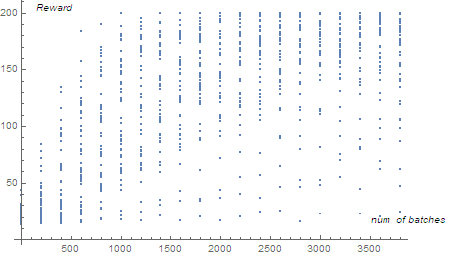
Situation for A2C is less satisfying. The performance of A2C network I implemented is very unstable, overall it trains fast, the network usually converges within 300 batches of training data. But more than often the network will converge into a non-optimal state. The average reward of the converged state can be all sorts of numbers, from 30, 80 to 190 are all possible. When I track the Advantage $A_i$ , I found that it usually decrease very fast, which means the predicted reward is close to actual reward, but usually it does not necessarily mean that reward is getting better. In a word, it still needs further improvement.
Following is an example of CartPole agent before training and after simple Policy Gradient Training. First GIF represents a policy network without training, second GIF shows network after 3000 batch of simple Policy Gradient training, third GIF shows network after 400 batch of A2C style Policy Gradient training.
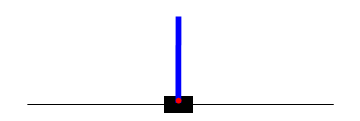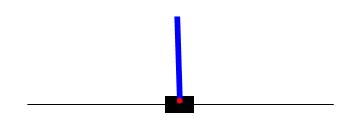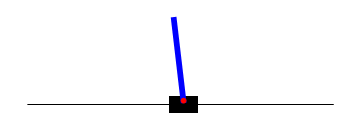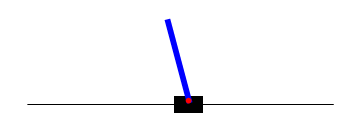
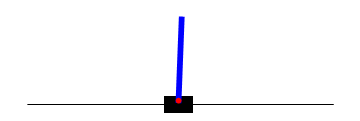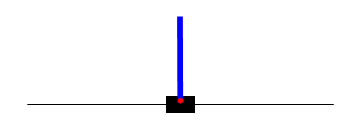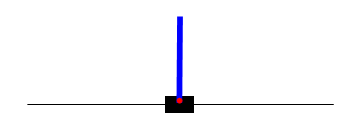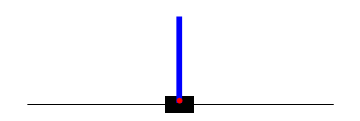
Future Work
The A2C style Policy Gradient that I implemented into the wolfram language is not having a good enough performance as expected, I will have to continue working on that and find potential source of error.
Also, I have started to train the network to play something more exciting than CartPole -- the Atari 2600 games. Currently, I'm using simple Policy Gradient in training agent to play "Pong". The difficulty in training it to play "Pong" comes from two aspects:
- The input from the environment is much bigger than Cartpole
- The game is much longer than CartPole and data generation is much slower.
- The reward in "Pong" is too sparse, the agent may generate thousands of observations and actions without a getting single positive rewar
There is a version of "Pong" on OpenAI gym: "Ram-Pong-v0" that did some pre-process of pixel image and turns every frame of image into a 128 vector, which makes the input much less complicated. However, it's still not easy enough for the network. What I tried is, instead of feeding the network the actual 128-vector of each frame, I took difference in between two frames so that most of the element in the 128-vector becomes zero. The next thing to try is to use a convolution layer instead of linear layer so that only important information (non-zero elements) will be kept.
I don't have enough time to complete the Policy Gradient training on Pong or other Atari games during this summer school. But the path is lit, that would be something interesting to do.