Chance Me: Predicting Chances of Getting Into Colleges Using Machine Learning and Clustering Techniques 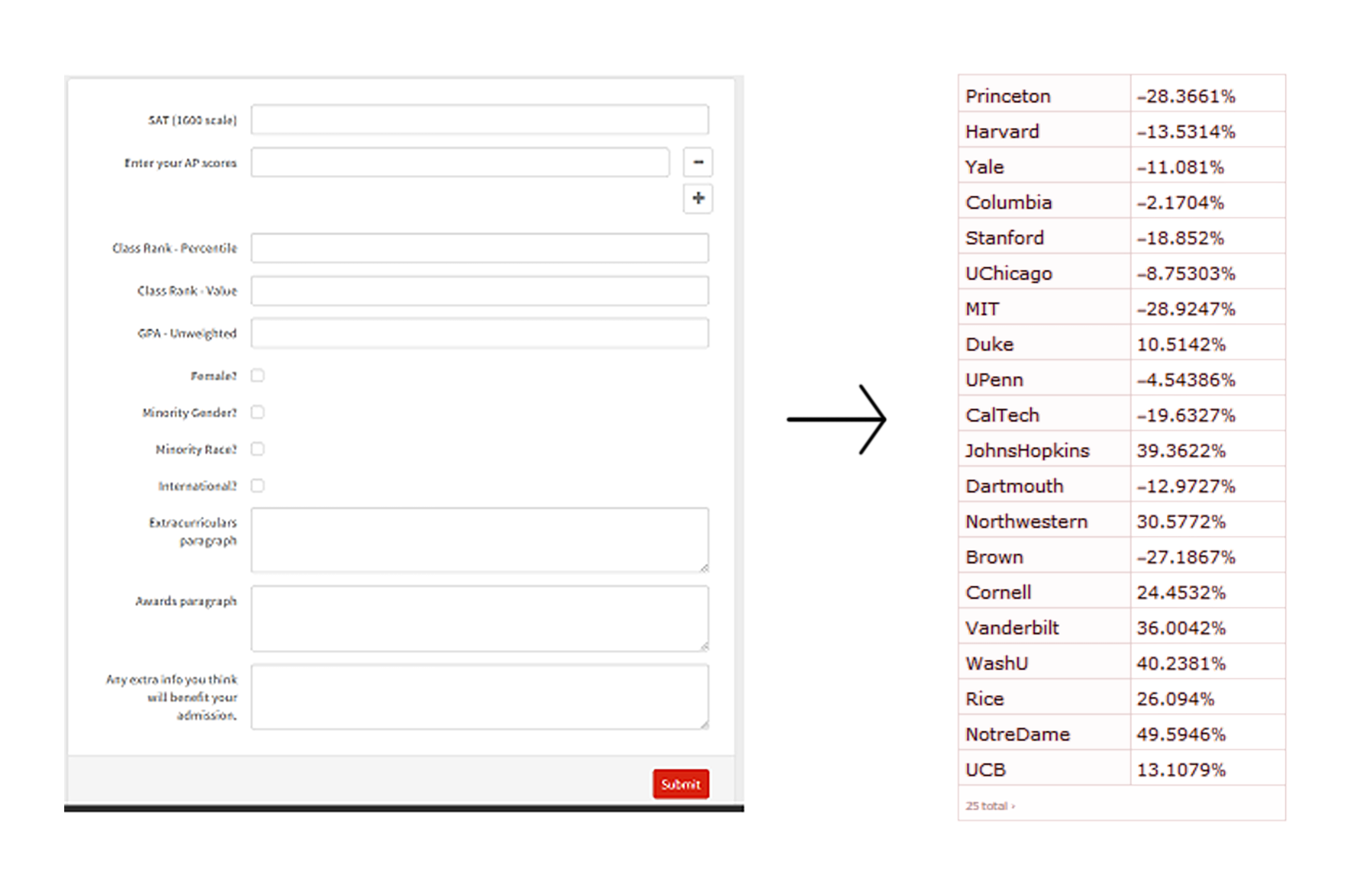
Goal of this project
Link to micro site to be added in future
The goal of this project is to predict acceptance into top colleges based on a variety of quantitative stats like SAT scores, GPA, AP scores, class rank, as quantitative data such as extracurriculars and awards using clustering techniques. Many teenagers are always very stressed about college admissions. This micro site and algorithm aim to decrease this stress by adding a way to quantitatively estimate the "chance" one has of getting into a specific college, as well as the predicted "accept"/"deny" status. Currently, there are very many websites that can do this similar prediction feature, but to my knowledge, there is not a single website that aims to incorporate non quantitative data (extra curriculars, awards..). In order to overcome limitations in neural network training because of over fitting, I propose a method that involves clustering data points using Word2Vec algorithm and the subsequent tally of data, which is further explained in the post below.
We will begin this problem by importing the datasets with the name of "students", "results", "collegesD". The format of these variables are lists of lists.
Next, the header is taken from the past results.
header = students[[1]]
header2 = results[[1]]
header3 = collegesD[[1]]
Next, we establish the data for the preparation of dataset.
data = students[[2 ;;]];
data2 = results[[2 ;;]];
data3 = collegesD[[2 ;;]];
To form the final dataset used for computation, the headers are taken and threaded onto the headers in order to create organized datasets.
studentsDataset = Thread[header -> #] & /@ data // Map[Association] ;
resultsDataset = Thread[header2 -> #] & /@ data2 // Map[Association] ;
collegesDataset = Thread[header3 -> #] & /@ data3 // Map[Association];
Next, some lookups are created to aid data processing.
lookup[__] = Null;
lookup2[__] = Null;
lookup3[__] = Null;
colleges = DeleteDuplicates[resultsDataset[All, "collegeID"]] ;
s = Map[#["studentID"] & , Normal[Dataset[studentsDataset][All, {1}]]];
c = Normal[colleges];
studentsDataset = Map[Association, Normal[studentsDataset]]
collegesDataset = Map[Association, collegesDataset];
Do[lookup[assoc["studentID"]] = assoc;, {assoc, Normal[studentsDataset]}]
Do[lookup3[assoc["collegeID"]] = assoc, {assoc , collegesDataset}]
Do[lookup2[assoc["studentID"]] = assoc, {assoc, studentsDataset}]
After that, functions for the bag of words are established. This method cleans data and creates a list of the most used words, sans the most common words. Originally, the algorithm didn't make use of any textual data, and RandomForest was only getting about a 68% accuracy. In order to improve the performance of the data, I opted to start increasing the usage of the extra data fields I have. However, these fields cannot be passed into the prediction function, as feature extraction is very difficult for large paragraphs. Therefore, a more advanced clustering method is adopted and described more in detail below.
bag[{KeyValuePattern[key_ -> _Missing]}, key_] := {}
bag[data__, part__] :=
Reverse[First /@
Sort[Tally[
DeleteStopwords[
Map[StringTrim[
StringDelete[
StringTrim[#], {"(", ")", "!", ".", "-", "_", ";", ",", "/", ":",
"'", "¡", "\t", "\r", "\n", "92s", "?s"}]] &,
Flatten[ToLowerCase[
StringSplit[
Flatten[Values[KeyTake[#, {part}] & /@ data]], {" ", ";", ":", "/",
"*"}]]]]]], #1[[2]] < #2[[2]] &]];
The bags are made for each of our text categories in the studentsDataset
bagOfWords = bag[Normal@studentsDataset, "activities"][[;; 10000]];
bagOfWordsAwards = bag[Normal@studentsDataset, "awards"][[;; 5000]];
bagOfWordsAdd = bag[Normal@studentsDataset, "addInfo"][[;; 5000]];
Next, clusters are made with these bags, and using the features found from Word2Vec. To increase the speed in the cloud, the 50 dimensional GloVe model is utilized, rather than the 300 dimensional Word2Vec model.
clusterModel =
ClusterClassify[bagOfWords, 300,
FeatureExtractor :>
NetModel["GloVe 50-Dimensional Word Vectors Trained on Tweets"]];
clusterModelAwards =
ClusterClassify[bagOfWordsAwards, 300,
FeatureExtractor :>
NetModel["GloVe 50-Dimensional Word Vectors Trained on Tweets"]];
clusterModelAdd =
ClusterClassify[bagOfWordsAdd, 300,
FeatureExtractor :>
NetModel["GloVe 50-Dimensional Word Vectors Trained on Tweets"]];
Next, a variable is assigned for the finalDataSet to be processed, as well as some data cleaning rules. Also, the finalDataSet is established with the data from the previously created lookups.
finalDataSet = <||>
resultsDataset = Map[Association, Normal@resultsDataset]
Do[
temp = clusterModel[bag[{lookup2[assoc["studentID"]]}, "activities"]];
temp2 = clusterModelAwards[bag[{lookup2[assoc["studentID"]]}, "awards"]];
temp3 = clusterModelAdd[bag[{lookup2[assoc["studentID"]]}, "addInfo"]];
finalDataSet[assoc["studentID"] <> assoc["collegeID"]] =
Merge[{lookup2[assoc["studentID"]], assoc,
lookup3[assoc["collegeID"]], <|
"act" -> Map[Count[temp, #] &, Range[300]]|>, <|
"awa" -> Map[Count[temp2, #] &, Range[300]]|>, <|
"addIn" -> Map[Count[temp3, #] &, Range[300]]|>}, Identity],
{assoc, resultsDataset}]
The data is cleaned using replacement rules.
replacements = {
{expr : _String | _Integer | _Real | _} :> expr,
s_String :> StringTrim[s],
s_String /; StringMatchQ[s, DigitCharacter ..] :>
RuleCondition@ToExpression[s],
s_String /;
StringMatchQ[s, DigitCharacter ... ~~ "." ~~ DigitCharacter ..] :>
RuleCondition@ToExpression[s],
s_String /;
StringMatchQ[s, DigitCharacter .. ~~ "." ~~ DigitCharacter ...] :>
RuleCondition@ToExpression[s],
"" -> Missing[],
Null -> Missing[],
s_String /; StringMatchQ[s, "Top " ~~ DigitCharacter .. ~~ "%"] :>
RuleCondition[
100 - ToExpression[
StringReplace[s, "Top " ~~ d : DigitCharacter .. ~~ "%" :> d]]],
s_String /; StringMatchQ[s, "Bottom " ~~ DigitCharacter .. ~~ "%"] :>
RuleCondition[
ToExpression[
StringReplace[s, "Bottom " ~~ d : DigitCharacter .. ~~ "%" :> d]]],
s_String /; StringContainsQ[s, "> 6"] :> 4.0,
i_Integer :> RuleCondition@N@i,
<|a___, "activities" -> x_Real, b___|> :> <|a, "activities" -> "", b|>,
"Doesn't Rank" | "No" | "Yes" -> Missing[],
l_List /; Total[l] == 0 :> Missing[]
};
cleanedUpData =
Values[KeyTake[#, inKeys]] -> Values[KeyTake[#, outKeys]] & /@
Values[Normal[finalDataSet]] //. replacements;
The data is split into a train and test list. Next, predict is used to create machine learning algorithm to do the actual prediction. Random Forest is used because it offers the best balance between over fitting and accuracy.
predict = Predict[train, Method -> "RandomForest"]
Discussion
Because the data for this problem is very prone to over fitting, the neural network was not an optimal fit for this problem. Therefore in order to generate quantifiable information out of the textual data, another method was used. In this specific option, a clustering method was chosen in order to create quantifiable information for the algorithm.
This process involves taking the most common words in each textual field and making a "bag" out of them. Then each bag is taken and features are extracted from the words using Word2Vec techniques. After that, the features taken out of the bag of words are clustered using the in built Mathematica function, which is applying K-means clustering to the set.
After these clusters are determined, the bag of words is no longer pertinent to the rest of the problem.
For the training set for the algorithm, the same "bag" algorithm is used to extract all of the pertinent words from the text fields. Finally, after the bag algorithm returns, it is once again clustered with the features extracted from the Word2Vec algorithm, in the clusters established earlier. Then the occurrences of each cluster are counted and encoded into a vector of 1 x N (clusters) and fed into the machine learning algorithm.
Conclusion
Using the clustering technique along with Random Forest algorithm, accuracy reached ~75-76 percent, which can be further increased by optimizing cluster sizing and bag sizing and word dimensional sizing. The project is deployed to a Wolfram Micro Site and is accessible to whoever would like to calculate their chances of getting into specific colleges.
Other Attempts
Originally, I attempted to gather data from College Confidential and parse through everyone's paragraphs in order to get the data for my machine learned algorithm. However, this became very difficult because formatting was very different for everybody. I was able to get the SAT/ACT/GPA scores, but anything beyond that was proving to be very challenging.
References: