Economics of Cryptokitties
Executive Summary
Cryptokitties is an online game run on the Ethereum blockchain that sells virtual cats with different "cattributes" (cat attributes). The goal of this project is to analyze what factors affect the price of a cryptokitty. The results from the gathered data show that certain cattributes can affect the price of a cryptokitty, but the scarcity of that cattribute does not seem to play a factor in determining a cryptokitty's price. The time a kitty was sold can be a contributor to the price of a cryptokitty, with cryptokitties that were sold soon after the game's launch tending to have higher prices than kitties sold at later times. Also, a kitty is most likely to be sold within the first two weeks of its birth.
Introduction
What are Cryptokitties?
Cryptokitties are virtual cats sold online using the Ethereum blockchain. Each cryptokitty has a certain set of cattributes, which is determined by their online genetic code. One cryptokitty is released every 15 minutes by the owners of Cryptokitties. While cryptokitties may be released by the company, cryptokitties can also breed, mixing up their genetic code and be creating new kitties that share cattributes passed down from its parents, and possibly even have a mutation that creates a new cattribute. When a person buys a cryptokitty online they own the rights to the genetic code of the cryptokitty, but the company owns the rights to all the images of the cryptokitty and all the programming that went into creating the virtual cat. One can buy a cryptokitty by visiting the Cryptokitties website and having an Ethereum wallet and buy a cryptokitty using ether, the Ethereum cryptocurrency.
Why should I care?
Blockchain technology will be an up-and-coming innovation that will change the way that people do online transactions. Blockchain technology is not just limited to the use of currency but can be applied to many different online fields, such as for games like Cryptokitties. Analyzing the economics Cryptokitties can help predict what a new wave of Blockchain games will look and operate like.
Gathering the data
To gather the data, I accessed the CryptoKittyDex website[1] and shifted between kitties by changing the cryptokitty's index number which is the last number in the URL.
ImportCryptoKittiesDB["Web", range_] :=
importRawKittiesData /@ (Range @@ range)
ImportCryptoKittiesDB["File", filepath_] := Import[filepath];
importRawKittiesData[id_] :=
Block[{request =
HTTPRequest[
URLBuild[{"https://cryptokittydex.com/kitties/", ToString[id]}]],
result},
result = URLRead[request];
If[result["StatusCode"] == 200, Import[result, "Data"]]
]
An obstacle I faced while doing this is that if I try to mass import cryptokitties, after some number of kitties there would be an error in importing data from a webpage, causing any importation after the failed import to never happen. To combat this problem I imported all kitties in random sets of eleven consecutive kitties and then pause for a few seconds before importing another set of kitties. This allowed for a break in the importation making new sets not crash due to and importation failure in an earlier set of kitties. I would flatten the gathered data so it'd be usable later, and then saved the data in a file in the case of my kernel crashing.
ranges = Table[With[{n = RandomInteger[825000]}, {n, n + 10}], 10];
sample72 = With[{range = #},
Pause[5];
ImportCryptoKittiesDB["Web", range]
] & /@ ranges;
cryptokittiesSample72 = Flatten[sample72, 1];
Save["/Users/kylekotanchek/Documents/CryptokittiesDatabases/\
CryptokittiesSample72.wl", cryptokittiesSample72]
Once a enough sets of data were gathered, I put them all into a database after deleting duplicates and any cases of failed imports which occurred in the form of Null.
database =
DeleteCases[
DeleteDuplicates[
Join[cryptokittiesSample1, cryptokittiesSample2,
cryptokittiesSample3, cryptokittiesSample[40],
cryptokittiesSample41, cryptokittiesSample42,
cryptokittiesSample43, cryptokittiesSample44,
cryptokittiesSample45, cryptokittiesSample46,
cryptokittiesSample47, cryptokittiesSample48,
cryptokittiesSample49, cryptokittiesSample50,
cryptokittiesSample51, cryptokittiesSample52,
cryptokittiesSample53, cryptokittiesSample54,
cryptokittiesSample55, cryptokittiesSample56,
cryptokittiesSample57, cryptokittiesSample58,
cryptokittiesSample59, cryptokittiesSample60,
cryptokittiesSample61, cryptokittiesSample62,
cryptokittiesSample63, cryptokittiesSample64,
cryptokittiesSample65, cryptokittiesSample66,
cryptokittiesSample67, cryptokittiesSample68,
cryptokittiesSample69, cryptokittiesSample70,
cryptokittiesSample71, cryptokittiesSample72]], Null];
Compiling the data
Once all the data was together, I was able to take certain parts of all of the data of the individual kitties and compile it in a usable way. I found the time a kitty was born, the generation of the kitty, the cattributes of the kitty, and the price and time the kitty was sold. A struggle found was that a kitty could have never been sold, sold once, or sold multiple times. Originally I ignored the cryptokitties that had never been sold, but later changed it to making their price zero after realizing this was causing price inflation in determining the average cost of a cryptokitty. Since every cat needed a time that it was sold at, I made cats that were never sold to have a selling data in 2016, which was before Cryptokitties was launched, so that it'd have no effect in analyzing the time vs. price distribution of sold cats. For every cryptokitty I paired the mean of all the prices a kitty was sold and paired that with each of its cattributes. I also made a function to see the average price value of a cattribute by taking the mean of all the prices of the cryptokitties that have the same cattribute. I dropped the last 15 items in the variable MeanCattributePrice because of some random kitties that never had their cattributes appear on the CryptoKittyDex website.
getPriceInfo[rawdata_] :=
Block[{data =
Cases[rawdata, {x_String, _} /; !
StringFreeQ[x, "Sold for"], \[Infinity]], rawprices, rawdates,
prices, dates}, rawprices = data[[All, 1]];
rawdates = data[[All, 2]];
prices =
Quantity[
ToExpression@
First[StringCases[#,
RegularExpression["Sold for ([[:print:]]+) ETH"] -> "$1"]],
"Ethers"] & /@ rawprices;
dates = DateObject /@ rawdates;
MapThread[List, {prices, dates}]]
GetKittyData[database_, id_Integer] :=
Catch[Block [{KittyData, KittySoldPrice, KittyBorn, KittyGeneration,
Cattributes, priceInfo},
(*832250 kitties*)
KittyData = database[[id, 2]];
priceInfo = getPriceInfo[KittyData];
If[priceInfo === {},
<|
KittyBorn ->
DateObject@
StringDrop[
StringReplace[KittyData[[1, 2]], "Born: " :> ""], -4],
KittyGeneration ->
StringReplace[KittyData[[1, 3]], "Generation: " :> ""],
Cattributes ->
StringSplit[
StringReplace[
StringReplace[KittyData[[1, 7]], "Cattributes: " :> ""],
" " :> ""], " , "],
KittySoldPrice -> {Quantity[0.0, "Ethers"],
DateObject[{2016, 1, 1}]}
|>,
<|
KittyBorn ->
DateObject@
StringDrop[
StringReplace[KittyData[[1, 2]], "Born: " :> ""], -4],
KittyGeneration ->
StringReplace[KittyData[[1, 3]], "Generation: " :> ""],
Cattributes ->
StringSplit[
StringReplace[
StringReplace[KittyData[[1, 7]], "Cattributes: " :> ""],
" " :> ""], " , "],
KittySoldPrice -> priceInfo
|>
]
]
]
CattributePricePK[database_, x_Integer] :=
Block[{list, price, kittydata = GetKittyData[database, x]},
If[Lookup[kittydata, KittySoldPrice] === {Quantity[0.`, "Ethers"],
DateObject[{2016, 1, 1}, "Day", "Gregorian", -4.`]},
{#, Quantity[0.`, "Ethers"]} & /@
First[StringSplit[Lookup[kittydata, Cattributes], ","]],
list = StringSplit[First[kittydata[[3]]], ","];
If[Length[ kittydata[[4]]] == 1, price = kittydata[[4, 1, 1]],
price = Mean[
Table[kittydata[[4, n]], {n, Length[kittydata[[4, 1]]]}][[All,
1]]]];
Table[{n, price}, {n,
If[Length[ kittydata[[4]]] == 1,
StringSplit[First[kittydata[[3]]], ","], list]}]
]
]
CryptoKittiesData[database_, id_, "FullInfo"] :=
GetKittyData[database, id]
CryptoKittiesData[database_, id_, "CattributesPrice"] :=
CattributePricePK[database, id]
CryptoKittiesData[database_, "CattributesMeanPrice"] :=
Block[{cattributesSet, cleandb = DeleteCases[database, Null],
dblength},
dblength = Length[cleandb];
cattributesSet =
Flatten[CryptoKittiesData[cleandb, #, "CattributesPrice"] & /@
Range[dblength], 1];
Mean[#[[All, 2]]] & /@ GroupBy[cattributesSet, First]
]
MeanCattributesPrice =
CryptoKittiesData[database, "CattributesMeanPrice"][[1 ;; -15]];
Finding Patterns
The first pattern I wanted to find was to see was if the scarcity of a cattribute is what determines the average value of the cattribute or if the scarcity of the cattribute isn't related to the cattribute's price. Due to some string importation errors in cattributes while compiling the cattribute-price relations, I had to find the cattributes that appeared in both the cattribute-price relations and in the cattribute-scarcity relation. Once I did that I then applied that intersection list to the cattribute-price and cattribute-scarcity relations to get two other lists that contained all of the cattributes shared between the two original lists.
completeCryptokittiesZeroSampleCounts =
Counts[Sort[
Flatten[Table[
Table[StringSplit[
StringSplit[
StringReplace[
StringReplace[database[[y, 2, 1]],
"Cattributes: " :> ""], " " :> ""], " , "][[7, 1]],
","][[x]], {x,
Length[StringSplit[
StringSplit[StringReplace[StringReplace[database[[y
, 2, 1]], "Cattributes: " :> ""], " " :> ""],
" , "][[7, 1]], ","]]}], {y, Length[database]}],
1]]][[15 ;; 198]]
listofSampleZeroCounts =
Table[{Keys[database][[x]], Values[database][[x]]}, {x,
Length[database]}]
listofSampleZeroMeanPrices =
Table[{Keys[MeanCattributesPrice][[x]],
Values[ MeanCattributesPrice][[x]]}, {x,
Length[MeanCattributesPrice]}]
intersectionofLists =
Intersection[listofSampleZeroCounts[[All, 1]],
listofSampleZeroMeanPrices[[All, 1]]]
intersectionofSampleZeroMeanPrices =
SortBy[Flatten[
Table[If[MatchQ[yay[[1]], nay], yay, Nothing], {yay,
listofSampleZeroMeanPrices}, {nay, intersectionofLists}], 1],
First]
intersectionofSampleZeroCounts =
Flatten[Table[
If[MatchQ[yay[[1]], nay], yay, Nothing], {yay,
listofSampleZeroCounts}, {nay, intersectionofLists}], 1]
Then I graphed the two resulting list by sorting all the cattributes in alphabetical order and placing it on the x-axis. For the first graph I showed the price in ethers on the y-axis, and in the second graph I showed how common each cattribute was on the y-axis.
BarChart[Transpose[intersectionofSampleZeroMeanPrices][[2]],
ChartLabels -> Automatic]
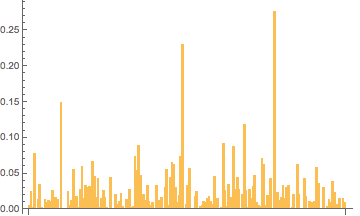
BarChart[Transpose[intersectionofSampleZeroCounts][[2]]]
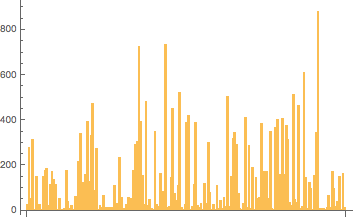
My hypothesis assumed that the two graphs would show an inverse relationship and that the price of a cattribute would originate from its scarcity, however the graphs showed no patterns between the two, proving my hypothesis to be wrong and proving there is no relationship between the scarcity of a cattribute and the cattribute's price.
We can also see Benford's Law apply to the first digit of the prices of the cryptokitties that were sold.
allPrices =
Flatten[Table[
If[getPriceInfo[database[[n]]] == {}, Nothing,
getPriceInfo[database[[n]]]], {n, Length[database]}], 1][[All,
1, 1]];
Histogram[
First@First[RealDigits[FractionalPart[#]*10]] & /@ allPrices]
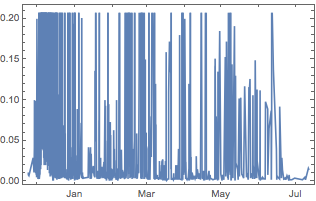
We can also see the price of cryptokitties sold over time. In the graph, we can see that cryptokitties sold soon after the game's release in November 28, 2017 to about January 2018 tended to be sold for higher prices than kitties sold in times after that period.
sortedDatesSold =
SortBy[Flatten[
Table[If[getPriceInfo[database[[n]]] == {}, Nothing,
getPriceInfo[database[[n]]]], {n, Length[database]}], 1], Last]
DateListPlot[
Thread[{sortedDatesSold[[All, 2]], sortedDatesSold[[All, 1]]}]]
Here is a microsite for looking up a cattribute and seeing what it's average price is and how common it is among kitties.
Link to Finding a Cattribute's Price and Commonality
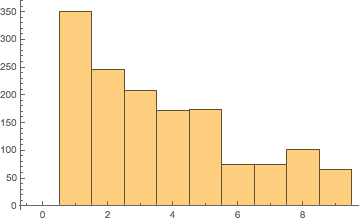
Some more information was found by Christian Pasquel using the same data and analyzing the time difference between when a kitty was born and sold. The variable data is the same thing as database, which was a variable used earlier.
data = Import[
FileNameJoin[{NotebookDirectory[], "cryptokittiesData01.wl"}]];
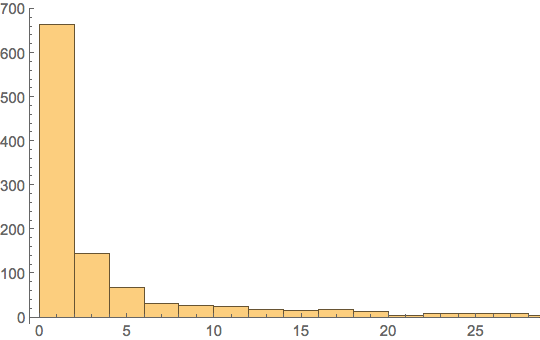
He then deleted all the kitties that had never been sold before and found the difference between the time that the kitty was born and the kitty was sold. The mean time of the difference of a kitty being born and sold was almost nine days, with many kitties being sold the same day they're born and some taking half a year to be sold since their birth; the longest difference in our dataset was 164 days. The histogram below shows the distribution of differences of cats being sold since being born.
In[170]:= soldCryptokitties =
DeleteCases[
data, <|__,
KittySoldPrice -> {Quantity[0.`, "Ethers"],
DateObject[{2016, 1, 1}, "Day", "Gregorian", -4.`]}|>];
Computing the time they stayed with her owners
In[171]:= timeBeforeLeaving =
Function[ck, (First[Sort[#[[2]][[All, 2]]]] - #[[1]]) &@
Lookup[ck, {KittyBorn, KittySoldPrice}]] /@ soldCryptokitties;
MinMax values
In[172]:= N@UnitConvert[MinMax[timeBeforeLeaving], "Days"]
Out[172]= {Quantity[0., "Days"], Quantity[164.849, "Days"]}
Mean time
In[173]:= UnitConvert[Mean[timeBeforeLeaving] // N, "Days"]
Out[173]= Quantity[8.93256, "Days"]
Histogram (in days)
In[174]:= Histogram[UnitConvert[timeBeforeLeaving, "Days"]]
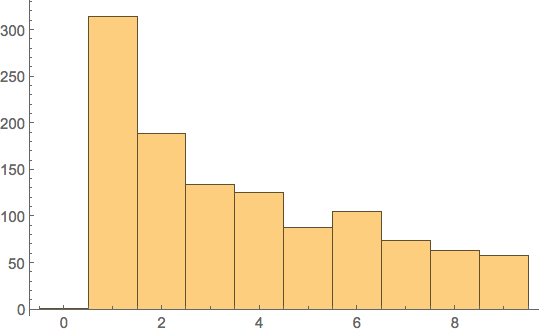
And Benford's Law still applies to the born-sold distribution.
Histogram[First[IntegerDigits[#[[1]]]] & /@ timeBeforeLeaving]
Future Work
Gathering more data into the dataset will be beneficial. Currently, there are only 3,112 cryptokitties inside the database, which are trying to represent over 840,000 kitties. Also looking more deeply into the relationships different traits that cryptokitties have will show more complex patterns. Some of these traits include whether the kitty has parents or not, what generation it is, the genetic code of the kitty, the kitty's description, and more.
Reference and other lists