I was assigned by Stephen Wolfram to create a sorting a network that could sort a specific list. To do this, I started by analyzing the optimal sorting network for a list of 16 items, which is in fact, the largest solution that humanity has found so far.

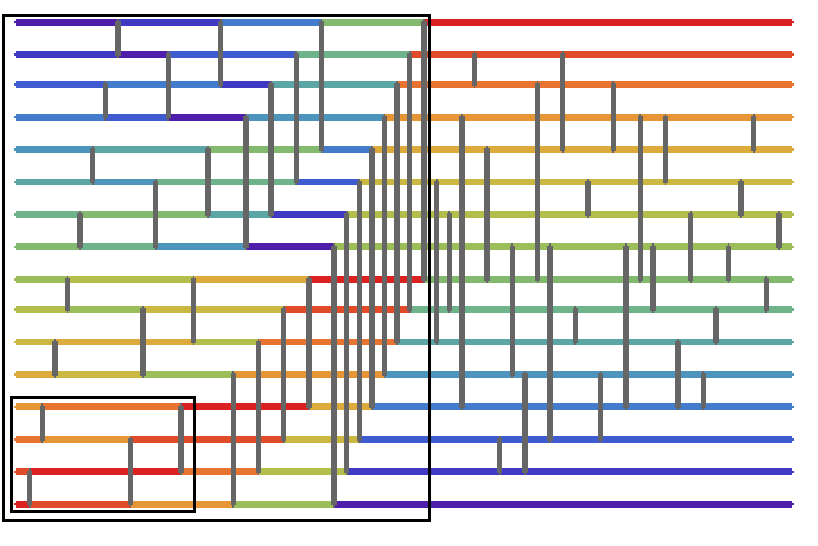
in the image above, there are two boxes, I noticed the pattern in the smallest of the two first, which in every optimal sort I checked, was used off the bat to group up sets of 4.

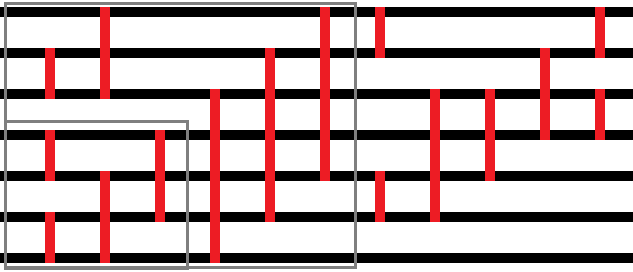
Next, by analyzing 14,15 and 16, 14, and 15 shown below.

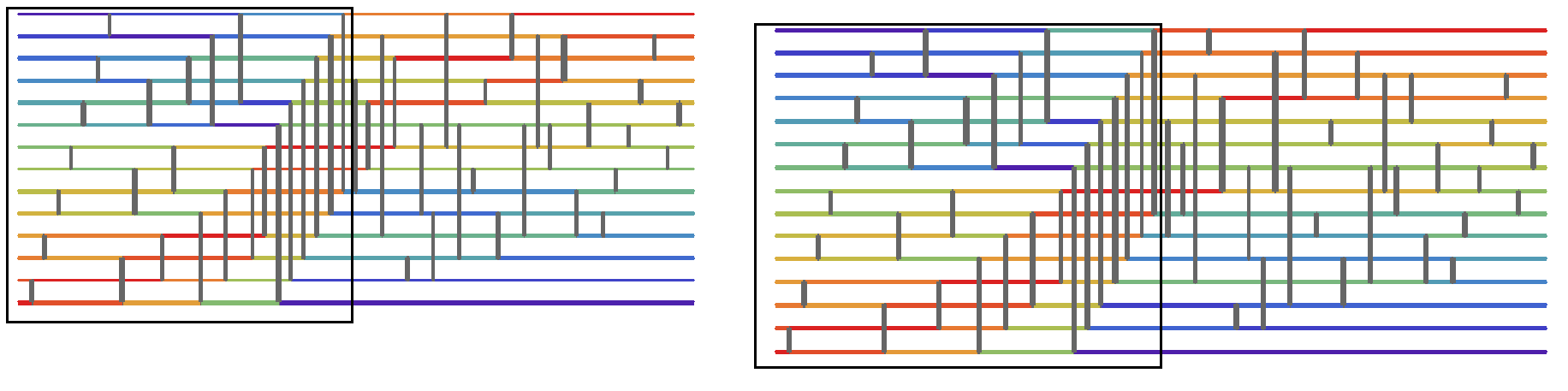
I derived a pattern for what was happening in the larger boxes, namely, there are beams of length 2^n or of the form {1+c,2^n+c} where c mod(2^(n+1)) <2^n. After this, I was prompted to create an algorithm that could automatically create a list of list of pairs that specified these connections. Essentially, I was looking for something of the form {{1,2},{3,4},{5,6},{7,8},{1,3},{2,4},{5,7},{6,8},{1,5},{2,6},{3,7},{4,8}}. The code to do this was complicated, though through perseverance I successfully did it. The code is shown below:

function1[distanceBetweenEle_, list_, finalList_] :=
 (Module[{arc, apair, apairamid, pairs},
   Partition[list, distanceBetweenEle, distanceBetweenEle];
   apair = 
    Part[Partition[list, distanceBetweenEle, distanceBetweenEle], 
     Span[1, -1, 2]];
   Map[{#, # + distanceBetweenEle} &, Flatten[apair]];
   apairamid = Map[
     Function[
      {itemInList},
      {itemInList, itemInList + distanceBetweenEle}
      ],
     Flatten[apair]
     ];
   pairs = Select[
     apairamid,
     Function[
      {item},
      Not[Part[item, 2] > Length@list]
      ]
     ];
   arc = Join[finalList, pairs];
   If [(Length[list] + 1 > distanceBetweenEle*2), 
    function1[distanceBetweenEle*2, list, arc], Return[arc];
    ]]) 

This was a great start. Though we now had to figure out what to do for the second half of the list. So let us take a look at the ends of the optimal algorithm for 14th 15 and 16 elements.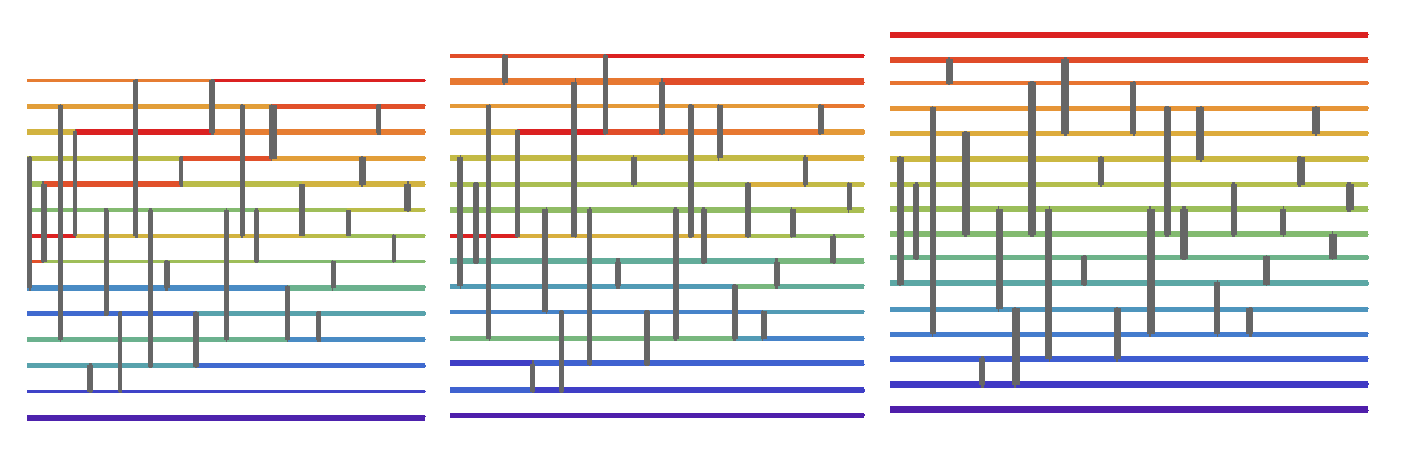

The first thing that most people should notice is that the connections follow no clear pattern. Despite this, there is one portion we will be able to exploit. If you look at the images above, you will notice that all new connections originated from the new segments. We can exploit this and proceed to only check connections from the old segment. The code for how I did this is below.

ClearAll[thingsToCheck]
thingsToCheck[L_, list_List, nope_] :=
Insert[list, {L, nope}, {#}] & /@ 
Prepend[(First /@ Position[list, L | 1] + 1), 1]
ClearAll[mainFunction]
mainFunction[L_, list_List] := 
Select[Flatten[thingsToCheck[#, list, L] & /@ Range[1, L - 1], 1] // 
DeleteDuplicates, Length[#] === Length[Split[#]] &]

Finally, I needed to implement a checker to check if the list could be sorted. No exploits were used for this segment, though in the future, presorting the first half could simplify the checker and would allow for greater number of checked permutations. The code is shown below.

ClearAll[swap]
swap[list_, {n_, m_}] :=
 If[list[[n]] > list[[m]],
  ReplacePart[
   list,
   {n -> Part[list, m],
    m -> Part[list, n]}
   ],
  list
  ]

ClearAll[allSwapInstructions]
allSwapInstructions[swapInstruc_, id_] :=
 Fold[swap, id, swapInstruc]

ClearAll[checker]
checker[swapInstruc_, L_, id_] :=
 Range[L] === allSwapInstructions[swapInstruc, id]

Finally, we devised a final code snippet that connected all previous codes segments together:

ClearAll[theOnesThatWork]
theOnesThatWork[list_List, len_, id_, firstHalf_] :=
 SelectFirst[Join[firstHalf, #] & /@ list,
  checker[#, len, id] &]

And we were done. Some testing is shown below:

id = {5, 2, 4, 1, 3}; step1 = mainFunction[5, {{2, 3}}] theOnesThatWork[step1, 5, id, function1[1, Range@5, {}]] step2 = Flatten[mainFunction[5, #] & /@ step1, 1]; theOnesThatWork[step2, 5, Reverse[Range[5]], function1[1, Range@5, {}]]

Special thanks to http://demonstrations.wolfram.com/SortingNetworks/