
Project Description
Graph coloring is an NP-complete problem that asks for the minimum number of colors required to color a graph such that no two adjacent vertices can have the same color. Because this is such a well-known topic, a lot of research has been done on it. However, not much study has been done on fractional colorings, which is simply a generalized graph coloring. What makes the fractional coloring problem complicated is that in addition to the problem constraint, each vertex is assigned a list of colors. So, the problem statement is as follows: "What is the minimum number of colors such that no two adjacent vertices have any colors in common?" Because each vertex can have varying number of colors, the infamous problem of fractional graph coloring is NP-complete. However, it can be reasonably approached through linear programming. In fact, the minimum real number to color a fractional graph while still satisfying the problem's constraints can be obtained as a solution to a linear program. In this project, I will be comparing two versions of the graph coloring problem: integral and fractional.
Definitions
$\textbf{Chromatic Number}$ [ $\chi(G)$ , $\chi^F(G)$]: Minimum number of colors required to color a graph while satisfying the coloring problem's constraints.
$\textbf{Chromatic Polynomial}$ [ $P(G, z), P(G^F, z)$]: Polynomial of order $n$ that counts the number of colorings as a function of the number of colors. Therefore, the minimum value that makes the function positive is the chromatic number.
$\textbf{a:b-coloring}$: Coloring that uses $a$ available colors to color a graph with $b$ vertices.
$\textbf{Graph Homomorphism}$: Mapping between two graphs that respects their structure.
$\textbf{Vertex-transitive graph}$: Graph such that every pair of vertices is equivalent under some element of its automorphism group.
Basic Methods
Below are the elementary methods purely pertaining to graph colorings:
ValidColoring[g_, c_] :=
AllTrue[Table[
Intersection[{c[[i]]}, c[[AdjacencyList[g, i]]]] == {}, {i, 1,
VertexCount[g]}], TrueQ];
ChromaticNumber[g_] :=
MinValue[{z, z > 0 && ChromaticPolynomial[g, z] > 0}, z, Integers];
The $\textit{ValidColoring}$ method ensures that the current list of colors satisfies the problem's constraint that no two adjacent vertices can have the same colors. It does so by checking that there are no intersections between each pair of adjacent vertices. The $\textit{ChromaticNumber}$ method goes through all integer values that make the chromatic polynomial of a graph positive and takes the minimum out of those values.
Fractional Colorings in Terms of Independent Sets
$I(G)$: set of all independent sets of vertices in $\textit{V(G)}$
$\textit{I(G,u)}$: set of all independent sets of vertices containing the vertex $u$
In this context, a fractional coloring is a mapping $f$: $I(G) \rightarrow$ [0, 1] with the property that, for every vertex $u$, $\sum_{J \in I(G,u)} f(J) \ge 1$. Then, the sum of the function values over all independent sets is called the weight of the fractional coloring. Therefore, the fractional chromatic number is the infimum of all the sums of the fractional coloring weights. To see the connection between fractional colorings and independent sets, one must note that each color class is an independent set belonging to $I(G)$. Then, define $f$: $I(G) \rightarrow$ [0, 1], mapping each color class to 1 and every other independent sets to 0. Next, suppose that a graph $G$ has a proper a:b-coloring. In this case, if one defines a function that sends each color class to $\frac{1}{b}$ and every other independent set to 0, it is true that $\sum_{J \in I(G,u)} f(J) = 1$ for every vertex $u$, which then leads to a fractional coloring with weight $\frac{a}{b}$.
Linear Programming Formulation
Below are the methods used to compute the fractional chromatic number:
independentSets[G_] := FindIndependentVertexSet[G, Infinity, All]
A[is_, G_] :=
Table[If[MemberQ[is[[i]], j], 1, 0], {i, Length[is]}, {j,
VertexCount[G]}]
OneVector[N_Integer] := Table[1, N]
y[one_, A_, R_] := LinearProgramming[one, Transpose[A], R]
From the relationship between chromatic numbers and independent sets, one can formulate a matrix $A(G)$ such that its columns are indexed by $V(G)$ and that its rows are indexed by $I(G)$. When formulating this matrix, entries are 1 if they are in the independent set represented by the column and 0 if they are not. Doing so essentially gives a characteristic function of the vertices' corresponding independent sets. Next, make a variable vector $y(G)$ that is indexed by $I(G)$. Then, the task reduces to minimizing the sum of the variables in the vector $y(G)$ (weighted coloring of graphs), subject to the set of constraints that each entry in $y(G)^T A(G) \ge 1$ and that all elements in $y(G)$ fall in the interval [0, 1].
Coloring the Graph
Idea
The $k$-fold chromatic number is given by $\chi(G) = \frac{1}{k}\chi(G')$, where $G'$ has each vertex in $G$ replaced with $k$ copies, and each edge $(u',v')$ in $G'$ is formed if the original vertices of both $u'$ and $v'$ in $G$ are the same or incident. This transformation is called strong graph product, which 'decomposes' each vertex into a complete graph $K_{k}$,while maintaining the overall structure of $G$. After coloring $G'$, group back all vertices that belong to the same 'super-vertex', which will lead $G$ to have multiple colors contributed by the sub-vertices in $G'$.
Methods
explodeGraph[g_, 1] := g
explodeGraph[g_, k_] :=
Graph[Union @@ newEdges[k] @@@ EdgeList[g]]
newEdges[k_][v1_, v2_] :=
With[{nv1 = Thread[{v1, Range[k]}], nv2 = Thread[{v2, Range[k]}]},
UndirectedEdge @@@ Join[
Tuples[{nv1, nv2}],
Subsets[nv1, {2}],
Subsets[nv2, {2}]
]
]
mapping[n_, g_, vstyle_, newmapping_] :=
Sort[Table[{newmapping[vstyle[[i]][[1]]], vstyle[[i]][[2]]}, {i,
Length[vstyle]}]]
FractionalColoring[n_Integer, m_Integer, cmaplist_] :=
Table[Graphics[{EdgeForm[Black],
Table[{cmaplist[[z]][[k]],
Disk[{0, 0},
1, {-\[Pi]/2 + 2 \[Pi]*(k - 1)/m, -\[Pi]/2 +
2 \[Pi]*k/m}]}, {k, 1, m , 1}]}], {z, 1, n, 1}]
Example with a cycle graph of 5 vertices ( $C_{5}$): 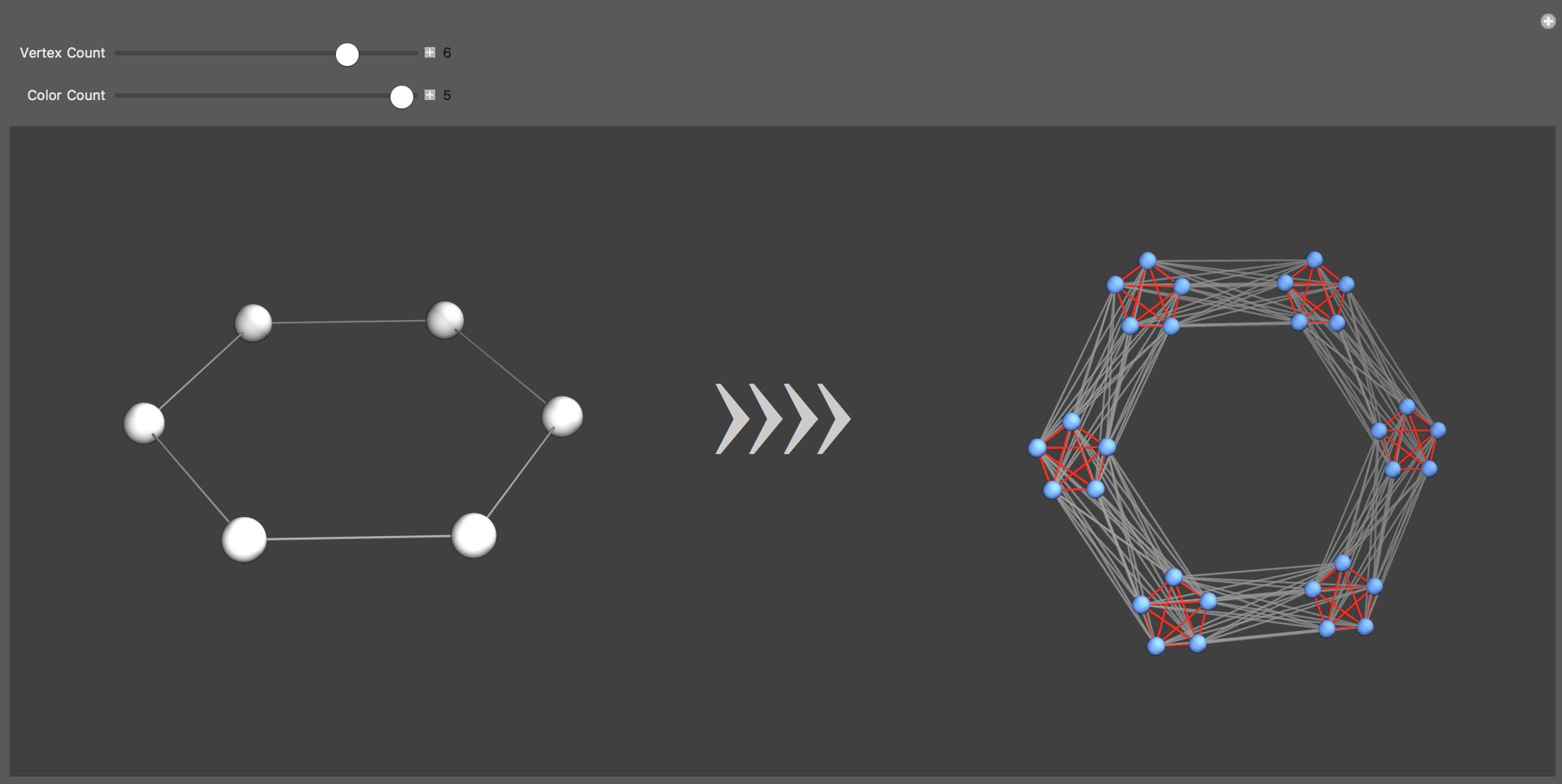
Special Graphs
Cycle Graph
Denoted by $C_{n}$, a cycle graph is a graph on $n$ nodes containing a single cycle through all nodes. Below is a cycle graph with 8 vertices. 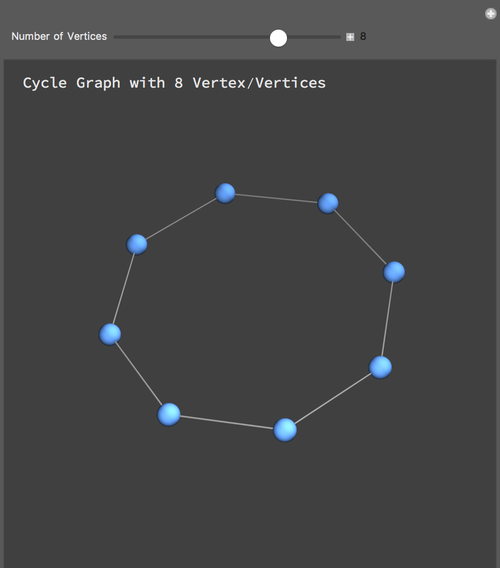
In a cycle graph, it is quite obvious that $i)$ if there are even number of vertices, then the chromatic number is 2, and $ii)$ if there are odd number of vertices, then the chromatic number is 3.
However, fractional graph coloring is slightly different. Although $\chi(G) = \chi^F(G)$ for even cases, that is not true for odd cases. In fact, $\chi^F (C_{2n + 1}) = 2 + \frac{1}{n}$. The fractional chromatic number in a cycle graph must be greater than 2 because four "one-half" colors must be used in any vertex triplets. Below is an example of 5:2-coloring of a cycle graph. 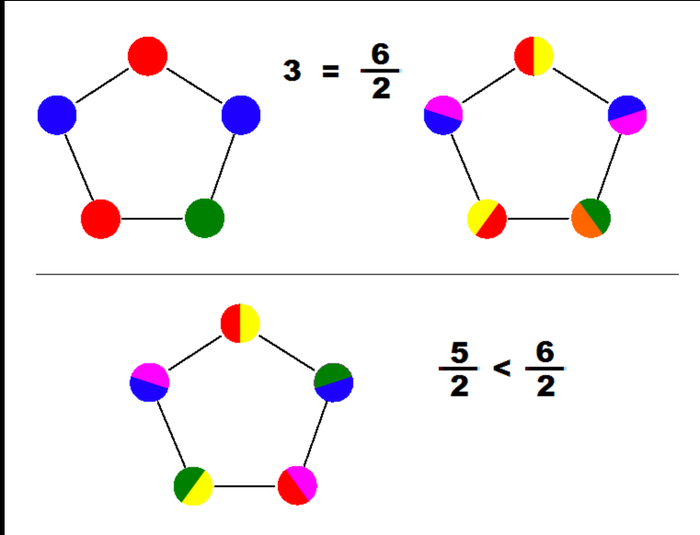
Kneser Graph
In a Kneser graph $K_{a:b}$, the vertices are $b$-element subsets of a fixed set $\{1, 2, ...., a\}$ and the edges exist between the vertices if and only if the subsets represented by them are disjoint. Therefore, by definition, if $b$ = 1, the graph becomes $K_{a}$, which is a complete graph with a vertices. The connection between graph coloring and graph homomorphism is that a graph is a:b-colorable if and only if there is a homomorphism $\phi : G \rightarrow K_{a:b}$.
Erdos-Ko-Rado Theorem states that: if $a$ and $b$ are positive integers with $a \ge 2b$, then independence number $\alpha(K_{a:b}) = {a-1\choose b-1}$. It is true that for any graphs, $\chi^F(K_{a:b}) \ge \frac{|V(K_{a:b})|}{\alpha(K_{a:b})}$. In the special case where the graph is vertex-transitive, $\chi^F(K_{a:b}) = \frac{|V(K_{a:b})|}{\alpha(K_{a:b})}$. Since there are ${a\choose b}$ vertices in a Kneser graph, $\chi^F(K_{a:b}) = \frac{{a\choose b}}{{a-1\choose b-1}} = \frac{a}{b}$.
Demonstration
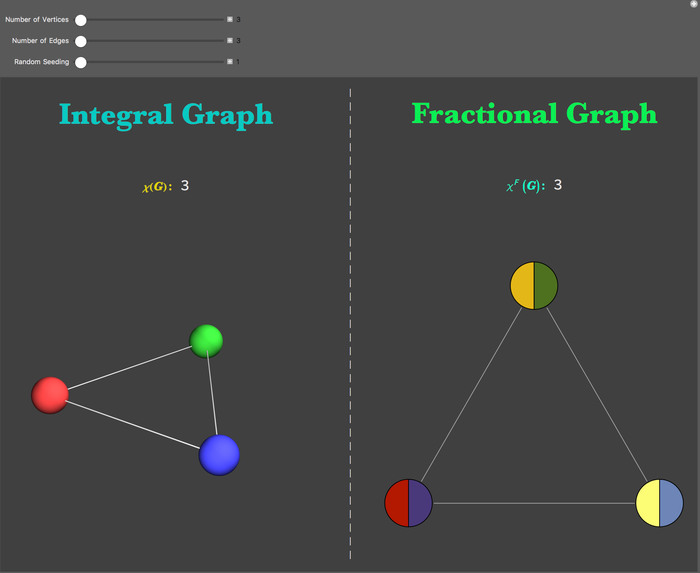
Below is the code for the Manipulate function that compares integral and fractional graph colorings:
Manipulate[
Module[{graph, graph2, chrom, colorings, sol, palette, cg, vL,
fracColoring, is, matrix, yV, fracChrom, fracG, vlist, map, fracC,
vstyle, newvl, newmapping, cmap, cmaplist},
SeedRandom[s];
graph = RandomGraph[{n, m}, VertexSize -> Medium];
graph2 = graph;
(* Integral Coloring *)
vL = VertexList[graph];
chrom = ChromaticNumber[graph];
colorings = Tuples[Table[i, {i, 1, chrom}], VertexCount[graph]];
sol = SelectFirst[colorings, ValidColoring[graph, #] &];
palette = discreteColors[chrom];
Do[PropertyValue[{graph, v[[1]]}, VertexStyle] = v[[2]], {v,
Table[{i, palette[[sol[[i]]]]}, {i, 1, VertexCount[graph]}]}];
(*Fractional Coloring *)
fracG = explodeGraph[graph2, 2];
vlist = VertexList[fracG];
newmapping =
Association[
Table[2*(vlist[[i]][[1]] - 1) + vlist[[i]][[2]] ->
vlist[[i]][[1]], {i, Length[vlist]}]];
newvl =
Table[2*(vlist[[i]][[1]] - 1) + vlist[[i]][[2]], {i,
Length[vlist]}];
fracG =
Graph @@ ({vlist, EdgeList[fracG]} /. Thread[vlist -> newvl]);
fracC = brelaz[fracG];
vstyle = MapIndexed[First[#2] -> ColorData[61, #1] &, fracC];
map = mapping[2, fracG, vstyle, newmapping];
cmap = Table[map[[i]][[2]], {i, Length[map]}];
cmaplist =
Table[cmap[[2*(i - 1) + j]], {i, 1, VertexCount[fracG]/2}, {j, 1,
2}];
fracColoring =
FractionalColoring[VertexCount[graph2], 2, cmaplist];
is = independentSets[graph];
matrix = A[is, graph];
yV = y[OneVector[Length[is]], matrix, OneVector[VertexCount[graph]]];
fracChrom = Total[yV];
Row[
{Column[{
Row[{Style["Integral Graph", Bold, RGBColor[0., 0.79, 0.76],
40, FontFamily -> "Baskerville"]}],
Row[{Style["Integral Chromatic Number: ", 15], Style[chrom, 20] }],
Graph3D[graph, ImageSize -> {400, 400},
EdgeStyle -> RGBColor[0.8, 0.8, 0.8]]
}, Center, 5],
Column[Table["|", {t, 1, 35}]],
Column[{
Row[{Style["Fractional Graph", Bold, RGBColor[0., 0.94, 0.33],
40, FontFamily -> "Baskerville"]}],
Row[{Style["Fractional Chromatic Number: ", 15], If[fracChrom < chrom, Style[fracChrom, 20, Bold, Pink],
Style[fracChrom, 20]]}],
Graph[graph2, ImageSize -> {400, 400},
VertexShape -> Thread[VertexList[graph2] -> fracColoring],
EdgeStyle -> RGBColor[0.8, 0.8, 0.8]]
},
Center, 5]},
" "
]
],
{{n, 3,
"Number of Vertices"}, 3, 7, 1, Appearance -> "Labeled"},
{{m, 3, "Number of Edges"}, 3, n*(n - 1)/2, 1,
Appearance -> "Labeled" },
{{s, 1, "Random Seeding"}, 1, 10000, 1, Appearance -> "Labeled"},
SaveDefinitions -> True
]
Future Work
First of all, the coloring process needs to be drastically optimized. Because the current algorithm is extremely slow, it cannot color a graph with more than 7 vertices. Initially, I hoped that I would be able to handle at least 100 vertices, but I realized that coloring a graph is not easy as it seems like. With further optimization, I hope to improve this project so that it can efficiently compute both integral and fractional chromatic number and optimally color both integral and fractional graphs almost instantly. Second of all, I wanted to explain the relationships between different topics of graph theory and graph colorings, but I was not able to do so because I spent too much time trying to figure out how to color a fractional graph. For instance, one of the most surprising characteristic of fractional chromatic number is that it is equal to the fractional clique number. Rigorously proving the previous statement requires deep insight into properties and characteristics of both fractional clique number and chromatic number, so doing so would make me digress and talk about tangential topics. Lastly, I want to handle more complicated fractional graphs, such as the ones that have more than just 2 colors assigned to them. In this project, each vertex is assigned 2 colors each. However, I want to expand on this project by having varying number of colors in each vertex. Moreover, the algorithm is not exact because I used the Brelaz heuristic, which is just an approximation of the coloring.
 Attachments:
Attachments: