Introduction

MMIX is a reduced instruction set computer designed primarily by Donald Knuth to use in his Art of Computer Programming. An MMIX computer contains 256 general registers labeled as register 0, register 1, register 2, register 3,....register 255. Each of the registers are used to store values from operations in programs. It also contains 32 special registers which each have a specific purpose unlike general registers which can be used to store values from any operation. For example the special register rR is used only for storing the remainder from the division operations. MMIX contains an array of $ 2^{64} $ byte. It has 256 built-in operation codes.

MMIX Architecture

The registers were represented as a list in which all values were initialized to 0.

registers={0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0}

The registers can be called on using the list take function. For example $0=registers[[1]] The special registers are also expressed as a 32 long list in which each of the values are initialized to 0. The special registers are called on using the list take function as well; each special register is associated with a position in the special registers list.

The memory is also represented as a 0 initialized list. Since $2^{64}$ is too large to make a list of that length and most programs don't use that much memory, the memory was set to $2^{16}$ bytes instead.

Each register can hold up to an octabyte(8 bytes) of memory.When a byte, wdye(2 bytes),tetra(4 bytes), or octa are represented by numbers,they are said to be either signed or unsigned. An unsigned byte is between $0$ and $2^8-1$, and a signed byte is between $-2^7$, and $2^7-1$. Similarly, an unsigned wyde is between $0$ and $2^{16}-1$, and a signed wyde is between $-2^{15}$, and $2^{15}-1$, an unsigned tetra is between $0$ and $2^{32}-1$, and a signed tetra is between$ -2^{31},$ and $2^{31}-1$, and an unsigned octa is between $0$ and $2^{64}-1$, and a signed octa is between $-2^{63}$, and $2^{63}-1$.

The operation codes can be split up into a few sections: Arithmetic, Bitwise operations, Bytewise operations, Floating Point operations and conversion, Conditional Branching, Loading and Storing, and Memory address operations. An example of a arithmetic operation code is addition. There are 4 operation codes for addition, each of which deal with different types of inputs. The addition operation codes deal with signed or unsigned numbers and also either a register or immediate value as the third argument. The addition operation codes are the following('U' stands for unsigned, and 'I' stands for Immediate 3rd argument.):

ADD is taking 3 register names, and setting the value of the first register to the sum of the 2nd and 3rd registers. ADDI does the same except the the 3rd argument is a number instead of a register name. Their unsigned counterparts do the same but cap the value of the first register at $2^{64}$.

Many of the Bit wise operations were emulated using the built-in bit functions of mathematica. These op-codes are the following:

A more unusual bitwise operation was the sideways add function which logically ands every bit of the 2nd argument with the complement of the 3rd argument and sets the result to the 1st argument which is a register name:

The bytewise operations deal with operating on corresponding bytes of two values. One example is the byte difference immediate function which sets the $jth$ byte of the first register to the difference of the $jth$ bytes of the second register and a constant:

An example of a float operation is square root: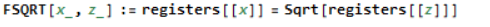

The loading functions load memory into the registers, and the storing operations do the opposite. Load byte is the following:

In MMIX there is the notion of a address in the location, and there is a current location in the memory. The variable 'location' is used to represent the current location. The operation LOC sets the current location in the memory which other operation codes use. The location of the specific strings are pre-defined locations in the memory.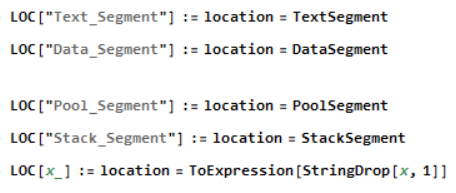

Run Program

That covers the architecture of the MMIX machine. The next step was creating a function that takes the MMIX code as a string and executes the code. To do this we needed a parse function; It splits the text at the line breaks and tabs:

Below is unparsed MMIX code, and then the parsed code in table form:

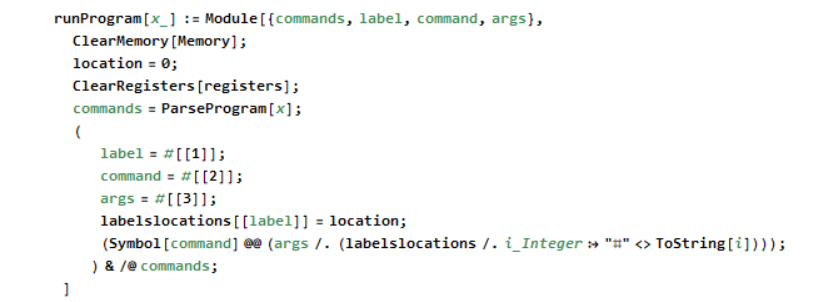
The parse program is used in the run program function. Run program splits the strings into the columns that MMIX code is in, and converts the strings of the operation codes and arguments into expressions and its evaluated:

Conclusions, Further Work

The successful part of this project was emulating the architecture of MMIX. All the main components of MMIX were implemented. The operation codes were not implemented completely, and the further work on this project will be to finish the rest of the operation codes, and see if there are any other ways of emulating the architecture of MMIX.