Let's share our Wolfram Language solutions of any arbitrary quiz/maths challenge which we found on the tube! I am not subscribed to such channels but once in a while, I would see a maths quiz video on my YouTube Recommendations page, for example, MindYourDecisions.
So how about this recent one: What Is The Area? "You Should Be Able To Solve This" 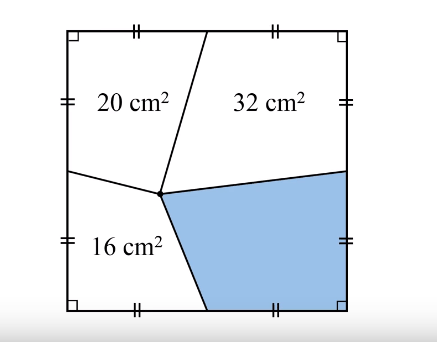
I am not interested in his analytical solution, tbh never watched the full video. I stopped the video right after the problem statement! I just want Mathematica to spit out the numerical (exact or approximate) solution. I've come so far:
In[1]:= r1 = Region@Polygon[{{0, 0}, {a/2, 0}, {x, y}, {0, a/2}}];
r2 = Region@Polygon[{{0, a/2}, {x, y}, {a/2, a}, {0, a}}];
r3 = Region@Polygon[{{a/2, a}, {x, y}, {a, a/2}, {a, a}}];
r4 = Region@Polygon[{{a/2, 0}, {a, 0}, {a, a/2}, {x, y}}];
eqs =
{Area[r1] == 16,
Area[r2] == 20,
Area[r3] == 32,
Area[r4] == a^2 - (16 + 20 + 32),
11 > x > 0, (* looking at the picture, I chose an estimated upper bound of 11 *)
11 > y > 0, (* bounding the variables should help the convergence of the numerical solver *)
11 > a > 0 (* but it is not always necessary to provide upper bounds *)
};
Then I've tried NSolve[ ], NMinimize[ ], FindInstance[ ], FindMinimum[ ] and only one of them worked. I must admit that I don't have much experience with these three functions and my PC's memory is limited too.
sol = FindMinimum[{0, eqs}, {x, y, a}, Reals] (* FAIL *)
sol = NSolve[eqs, {x, y, a}, Reals] (* FAIL *)
sol = FindInstance[eqs, {x, y, a}, Reals] (* FAIL *)
In[6]:= sol = Last@NMinimize[{0, eqs}, {x, y, a}, Reals] (* {x -> 2.44949, y -> 4.08248, a -> 9.79796}} *)
Out[6]= {x -> 2.44949, y -> 4.08248, a -> 9.79796}
In[7]:= Area[r4] /. sol
Out[7]= 28.
Whenever you come across a youtube quiz and solved it as a recreational task, please share it here, it's much fun!