I am using Mathematica 10.3. I want fo perform a computational analysis of the motion of the Earth around the sun based on Keplers laws. Here is my code so far.
eulerStep[{t_, state_List}, h_, f_List] := {t + h,
state + h Through[f[{t, state}]]}
solveSystemEuler [{t0_state0 _}, h_, n_Integer, f_List] :=
NestList[eulerStep[#, h, f] &, {t0, state0}, n]
midptStep[{t_, state_List}, h_, f_List] := {t + h,
state + h Through[
f[{t + 1/2 h, state + 1/2 h Through[f[{t, state}]]}]]}
solveSytemMidPt[{t0_, state0_}, h_, n_Integer, f_List] :=
NestList[midptStep[#, h, f] &, {t0, state0}, n]
L = 1/2 m (x'[t]^2 + y'[t]^2) + GMm/Sqrt[x[t]^2 + y[t]^2];
D[D[L, x'[t]], t] - D[L, x[t]] == 0
D[D[L, y'[t]], t] - D[L, y[t]] == 0
xdot[{t_, {x_, vx_, y_, vy_}}] := vx
vxdot[{t_, {x_, vx_, y_, vy_}}] := -x/(x^2 + y^2)^(3/2)
ydot[{t_, {x_, vx_, y_, vy_}}] := vy
vydot[{t_, {x_, vx_, y_, vy_}}] := -y/(x^2 + y^2)^(3/2)
start = {1, 0, 0, 1};
fcns = {xdot, vxdot, ydot, vydot};
orbit = solveSystemEuler[{0, start}, 0.01, 800, fcns];
<< Statistics`DataManipulation`
xypts = Column[Column[orbit, 2], {1, 3}];
ListPlot[xypts, PlotJoined -> True];
Running the program gave the following error messages. 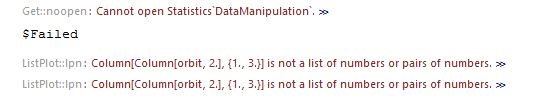
Please help me to fix my code.