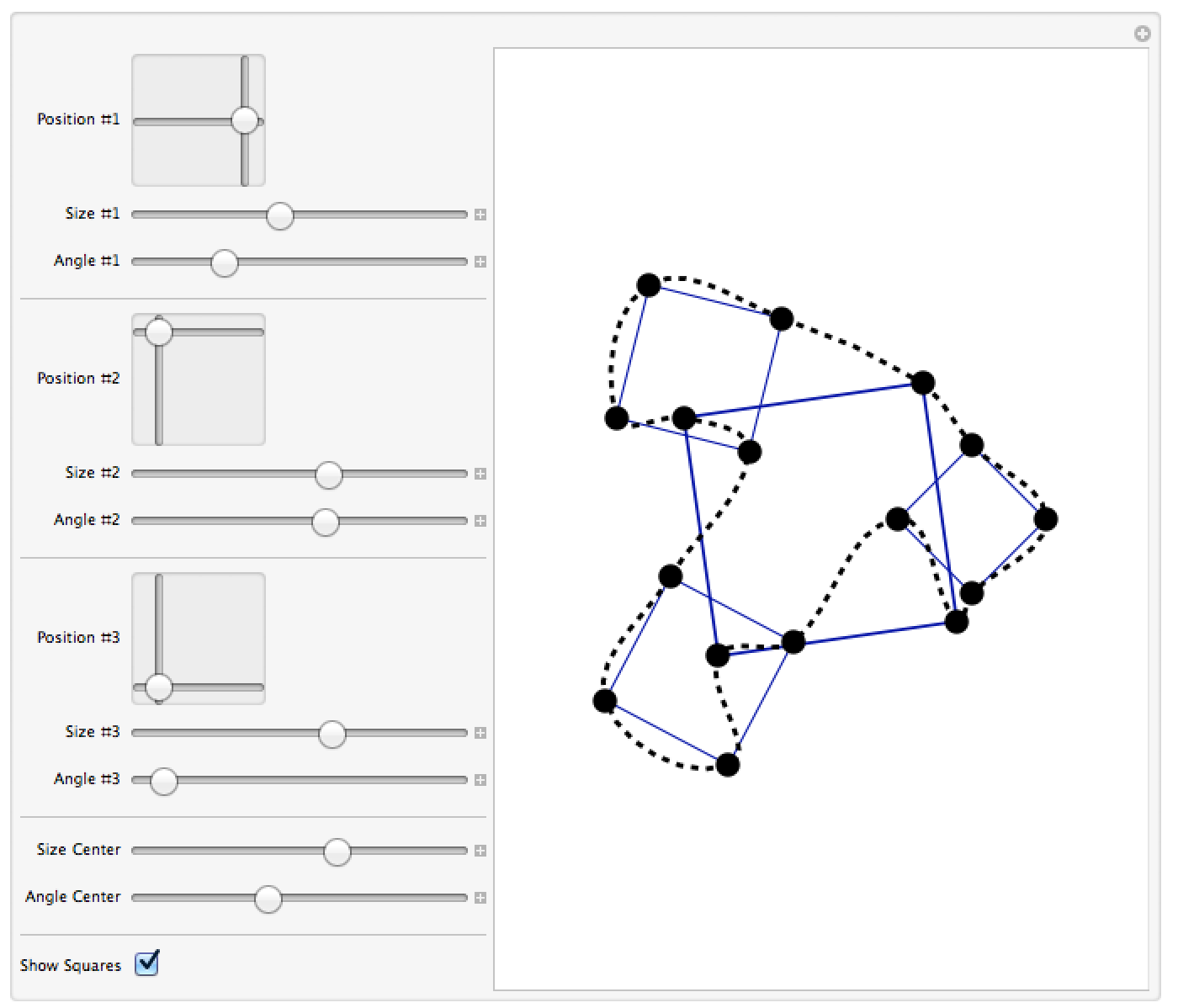
Here I made the interactive example:
ClearAll[CreateSquare,CreateScene]
CreateSquare[p:{px_,py_},L_,\[Theta]_]:=With[{\[Phi]=Range[0,3\[Pi]/2,\[Pi]/2]+\[Theta]}, {px+Cos[\[Phi]]L/2,py+Sin[\[Phi]]L/2}\[Transpose]]
CreateScene[p:{p1_,p2_,p3_},L:{l1_,l2_,l3_,l4_},\[Theta]:{\[Theta]1_,\[Theta]2_,\[Theta]3_,\[Theta]4_},showsqrs_]:=Module[{plg,allpoints,order,smooth},
plg=MapThread[CreateSquare,{Append[p,{0,0}],L,\[Theta]}];
allpoints=Flatten[plg,1];
order=FindShortestTour[allpoints][[2]];
allpoints=Part[allpoints,order];
smooth=BSplineCurve@{#2,#2+Normalize[#3-#] Norm[#3-#2]/3,#3-Normalize[#4-#2] Norm[#3-#2]/3,#3}&@@@Partition[allpoints,4,1,{2,2}];
If[showsqrs,
Graphics[{EdgeForm[{Darker@Blue,Thickness[0.003]}],FaceForm[None],Polygon[Most@plg],{EdgeForm[Thickness[0.005]],Polygon[Last@plg]},Black,PointSize[0.04],Point[allpoints],CapForm[None],Dashing[0.0125],Thickness[0.008],smooth},PlotRange->2]
,
Graphics[{Black,CapForm[None],Dashing[0.0125],Thickness[0.008],smooth},PlotRange->2]
]
]
Manipulate[
CreateScene[{p1,p2,p3},{size1,size2,size3,size4},{\[Theta]1,\[Theta]2,\[Theta]3,\[Theta]4},show]
,
{{p1,{1,0},"Position #1"},{-1,-1},{1,1}},
{{size1,0.98,"Size #1"},0.2,2},
{{\[Theta]1,1.57,"Angle #1"},0,2\[Pi]},
Delimiter,
{{p2,{-0.8,1},"Position #2"},{-1,-1},{1,1}},
{{size2,1.28,"Size #2"},0.2,2},
{{\[Theta]2,3.68,"Angle #2"},0,2\[Pi]},
Delimiter,
{{p3,{-0.8,-1},"Position #3"},{-1,-1},{1,1}},
{{size3,1.3,"Size #3"},0.2,2},
{{\[Theta]3,0.3,"Angle #3"},0,2\[Pi]},
Delimiter,
{{size4,2.25,"Size Center"},1,3},
{{\[Theta]4,0.21,"Angle Center"},0,2\[Pi]},
Delimiter,
{{show,True,"Show Squares"},{True,False}}
]
giving: