Recently
Ed Pegg shared an interesting research about
constriction of complex mazes by computers that are influenced by some human designs. I was curious how Mathematica will do in automated maze solving of this type. I grabbed a screenshot of the following maze:
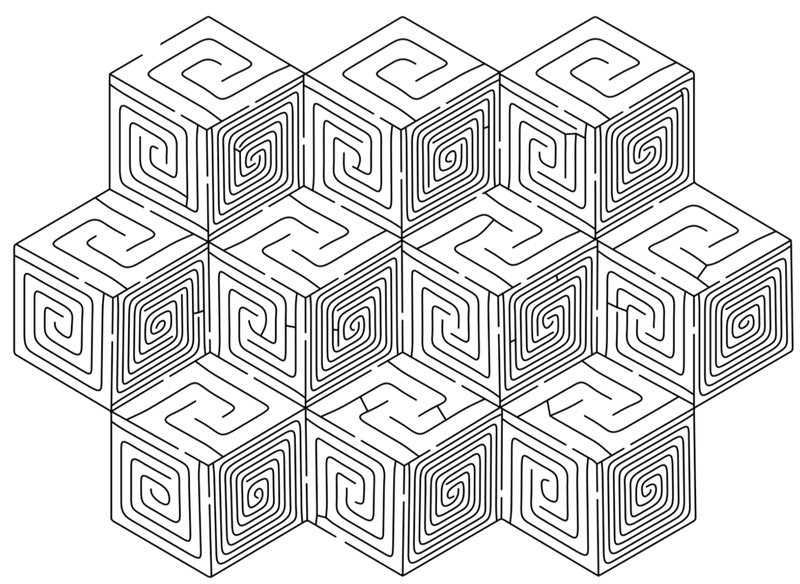
Because this image will now be stored on Wolfram Community servers we can use its URL to import it to Mathematica:
img = Import["http://goo.gl/IUUtVC"];
In WL I am aware of two ways to solve a maze: using
WatershedComponents and using
Pruning. The code is really minimal and here are the results:
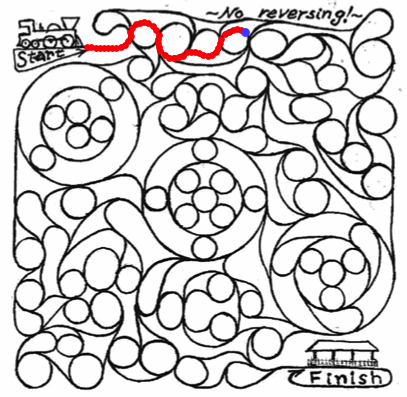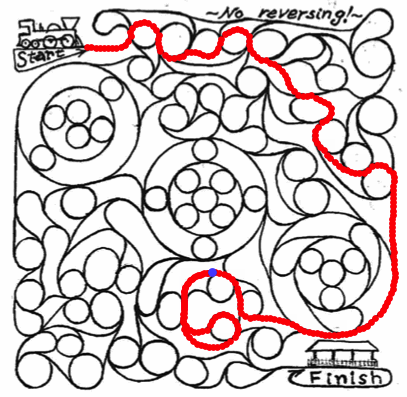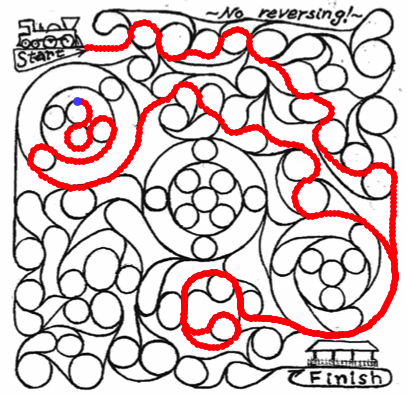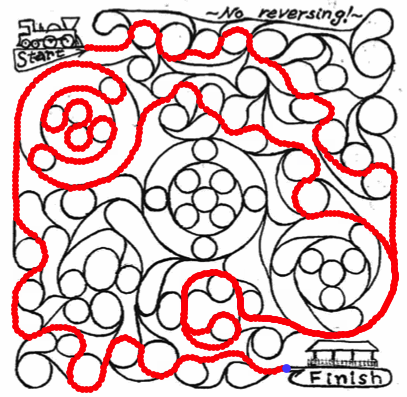
sol1 = Image[Clip[1 - WatershedComponents[Binarize@img], {0, 1}]];
HighlightImage[img, Dilation[sol1, 1], "HighlightColor" -> Red]

sol2 = Pruning[Thinning[Binarize@img], Infinity];
HighlightImage[img, Dilation[sol2, 1], "HighlightColor" -> Red]

These implementations find all possible solution paths and we can actually check that the solutions are identical:
HighlightImage[sol2, Dilation[sol1, 2]]

Is anyone aware of any other methods? By the way take a look at some
great maze Demonstrations our users crated. These include also maze-generation algorithms. A very memorable Demonstration is by Antonin Slavik and
Stan Wagon:
Penrose's Railway Mazes - see animation below. Share your own experience with WL and mazes!