For those of you who don't have an Arduino but are still willing to inject computation to Homer Simpson

I devised the following method to emulate an accelerometer using a webcam:
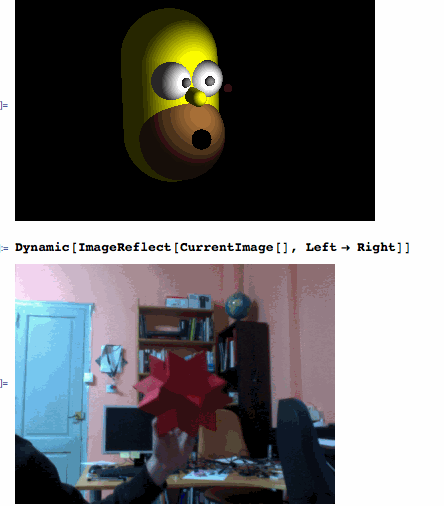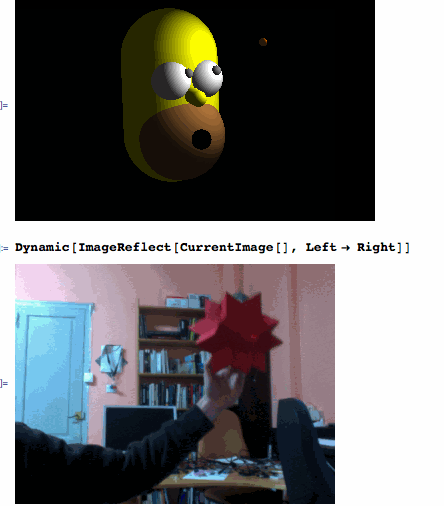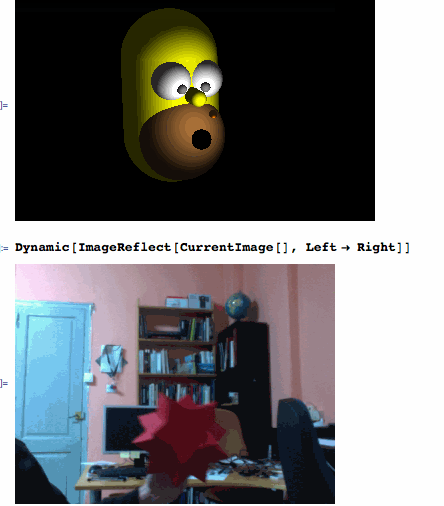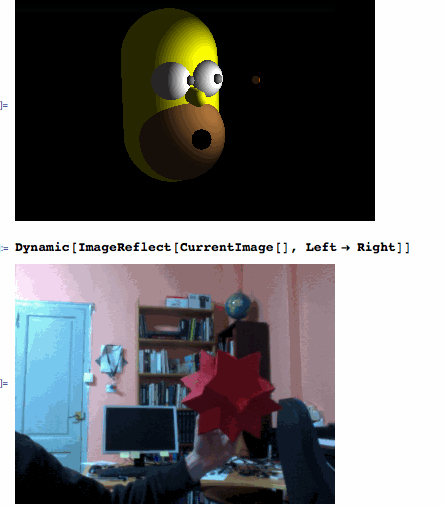
redXYZ[x_] := {Divide[35 - x[[2]], 35], Divide[50 - x[[1]], -35], Divide[20 - x[[3]], 20]}
RunScheduledTask[
bee = redXYZ[Flatten[ReplaceAll[1,
ComponentMeasurements[
ColorNegate[
CommonestFilter[
Binarize[
ImageApply[If[#[[1]] > #[[2]] + #[[3]], #, {1, 1, 1}] &,
ImageReflect[ImageResize[CurrentImage[], 100], Left -> Right]]
],2]],
{"Centroid", "EquivalentDiskRadius"}]]]], 0.4]
After filtering the red object from the CurrentImage[], ComponentMeasurements' "Centroid" is giving the XY coordinates and "EquivalentDiskRadius" provides the depth Z. Then, redXYZ[] calibrates the coordinates of the "bee" that is being refreshed every 0.4 seconds by the ScheduledTask.
If a red object is being detected correctly...
Dynamic[bee]
... then, you are ready to have fun playing with Homer:
Graphics3D[{Orange, Sphere[Dynamic[4*bee], 0.2], White, Sphere[eyeL = {0.1, 0.9, -2}, 1], Sphere[eyeR = {0.1, -0.9, -2}, 1], Gray, Sphere[Dynamic[Normalize[4*bee - eyeL] + eyeL], 0.25], Sphere[Dynamic[Normalize[4*bee - eyeR] + eyeR], 0.25], Yellow, Tube[{{-1, 0, -4}, {3, 0, -4}}, 2.5], Tube[{{0.8, 0, -1.8}, {1, 0, -0.8}}, 0.4], Brown, Sphere[{3, 0, -3}, 2.3], Black, Sphere[{3, 0, -0.65}, 0.5]}, Lighting -> {{"Ambient", GrayLevel[.15]}, {"Point", White, Dynamic[4.5*bee]}}, ViewPoint -> {-0.32, -1.8, 3.6}, ViewVertical -> {-1.44`, 0.12`, -0.2`}, PlotRange -> {{-4, 5.5}, {-7, 7}, {-7.5, 4}}, Background -> Black, Boxed -> False]