Probably it is worth to mention that with your approach you obtain an interpolated radial intensity values, not the actual pixel intensity values from the original image. This difference is subtle and may be OK or may be not depending on the final goal. Both my solutions produce radial profile consisting from actual pixel intensity values of the original image, no interpolation is used.

You may be interested in this solution which is also based on ImageTransformation but takes care to avoid interpolation. The only drawback is that it does not allow to get the actual distances between the pixels and the center (these distances are not uniform in the general case). Again, it may be OK depending on what the final goal is.

One thing that I suggest you to take into account is the color profile with which your image is encoded. For the applications in physics it is crucial whether the color intensity values of your image are proportional to the actual light intensities recorded by your photoelectronic device or they are transformed into a "gamma-corrected" and hence non-additive derivatives. With non-additive values any interpolation scheme produces misleading results.

Sorry for the lack of labels.... "a" is the angle of the line, "w" is the width (in degrees) of the section of the image. If you modify the parameters in the Manipulate, you will see immediately how they relate to the radial section of the image.

The curves are: Min, Max, and Mean of the data, summed over the angular width w, for each radius (from 0 to 500 here). The bottom curve (in red) is the Standard Deviation of the data for each radius.

The idea was to demonstrate that once the image is transformed in polar coordinates, you can compute a lot of useful radial information in real time.

Antonio,

Here is a solution based on the Bresenham's algorithm implemented by halirutan:

bresenham[p0_, p1_] := Module[{dx, dy, sx, sy, err, newp},
  {dx, dy} = Abs[p1 - p0];
  {sx, sy} = Sign[p1 - p0];
  err = dx - dy;
  newp[{x_, y_}] := 
   With[{e2 = 2 err}, {If[e2 > -dy, err -= dy; x + sx, x], 
     If[e2 < dx, err += dx; y + sy, y]}];
  NestWhileList[newp, p0, # =!= p1 &, 1]
];

Since Bresenham's algorithm requires integer pixel positions for both ends of the line we have to snap the line to the pixel grid in the coordinate system used by PixelValue which differs from the standard image coordinate system by 1/2:

\[Alpha] = Pi/4;
radius = 300;

crcl = ComponentMeasurements[RegionBinarize[Dilation[img, 3], {{600, 440}}, 0.5], 
   "Centroid"];
(* centroid in the standard image coordinate system *)
center = 1 /. crcl;
(*integer position of the central pixel in the coordinate system used by PixelValue*)
centralPixelPosition = Round@N[center + 1/2];
(*integer position of the ending pixel in the coordinate system used by PixelValue*)
endingPixelPosition = Round@N[AngleVector[centralPixelPosition, {radius, \[Alpha]}]];
radialPixelPositionsBresenham = bresenham[centralPixelPosition, endingPixelPosition];
radialProfileBresenham = 
  Transpose[{Map[N@EuclideanDistance[centralPixelPosition, #] &, 
     radialPixelPositionsBresenham], PixelValue[img, radialPixelPositionsBresenham]}];

model = a/b Erfc[(-x + \[Mu])/(Sqrt[2] \[Sigma])];
fit = FindFit[radialProfileBresenham, model, {a, b, \[Mu], \[Sigma]}, x];
Row[{Show[ListLinePlot[radialProfileBresenham, ImageSize -> Medium], 
   Plot[model /. fit, {x, 0, radius}, PlotStyle -> Red, PlotRange -> All, 
    Evaluated -> True]], 
  Show[img, Epilog -> {Red, Thickness[.01], 
     Arrow[{centralPixelPosition - 1/2, endingPixelPosition - 1/2}], 
     Circle[centralPixelPosition - 1/2, radius]}, ImageSize -> Small]}]

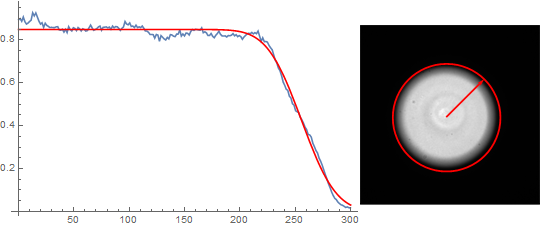
Also find attached updated version of your Notebook.

Attachments:

Dear Alexey, All solutions are good. If you allow me I would like to add one more requirement. I have tried, but my knowledge is still not enough to solve it in a short time. It would be interesting if it were possible to use the image center (prior calculation of the centroid). Also interesting would finish line profile in a circle of radius r. I have tried adapt a small routine in attachment without success until now. Thank you anyway

Antonio

Attachments:

Hi Antonio,

Here is one approach:

\[Alpha] = Pi/3;
id = ImageDimensions[img];
pr = {0, #} & /@ id;
center = Mean /@ pr;
gr = Graphics[{White, AbsoluteThickness[1], 
    Line[{center, AngleVector[center, {Norm[id], \[Alpha]}]}]}, Background -> Black, 
   PlotRangePadding -> None, ImageSize -> id, PlotRange -> pr, AspectRatio -> Automatic];
mask = Binarize@Rasterize[Style[gr, Antialiasing -> False], "Image"];
radialProfile = 
  PixelValue[img, SortBy[PixelValuePositions[mask, 1], N@EuclideanDistance[center, #] &]];
Row[{ListLinePlot[radialProfile, ImageSize -> Medium], Show[img, gr /. White -> Red]}]

I also attach updated version of your Notebook to this post.

Attachments: