Hi,

same idea. Again the right hand side has to be zero. The Bessel function does not make this easier, but it is possible to get this numerically.

It is a good idea to first plot the right hand side - setting x[t-15] and x[t] simply to x.

Plot[(1/4) BesselJ[1, x] - x/10, {x, -5, 5}]

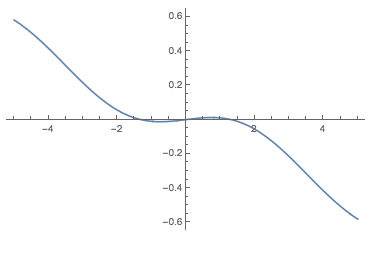
So, it looks as if there are three zeros: one at 0 one close to 1 and one close to -1.

We can get that in one line:

FindRoot[(1/4) BesselJ[1, x] - x/10 == 0, {x, {-1, 0, 1}}]

where the -1,0,1 are the starting values for our search. We obtain:

({x -> {-1.31102, 0., 1.31102}})

so three fixed points. If you are unhappy about guessing the first points, you can start at lots of random starting points:

ToExpression /@ DeleteDuplicates[ToString /@ Chop[FindRoot[(1/4) BesselJ[1, x] - x/10 == 0, {x, #}]] & /@ RandomReal[{-10, 10}, 100]]
(*{{x -> -1.31102}, {x -> 0}, {x -> 1.31102}}*)

The ToString and ToExpression step is not nice, but otherwise DeleteDuplicates does not work.

Cheers,

Marco