Supercapacitors, sometimes called ultracapacitors or electric double-layer capacitors (EDLC), have high power density and can charge and discharge very quickly if needed. This is a good thing if you are trying to capture the energy from a braking system, or if you only have a few minutes to charge a cell phone before heading out. Traditional Li-ion batteries have higher energy density, but lower power density and take a longer time to charge and discharge.
They have several applications such as electric vehicles, power tools, hand-held devices, uninterruptible power supplies, and many others. Thus it is very useful to be able to create re-usable mathematical models for them. In this post, I'll look at how we can create fast and versatile Modelica models for supercapacitor simulation and analysis with SystemModeler and Mathematica.
Let's dive in! The first basic model I'll create is one where we'll use a large capacitor, a resistor in series and a resistor in parallel.
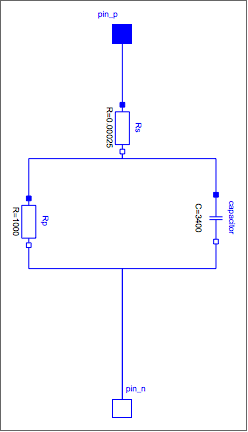
The resistor in series represents the internal resistance. The resistance in parallel represents the leakage current. This circuit is sometimes called the "Classical Equivalent Circuit".
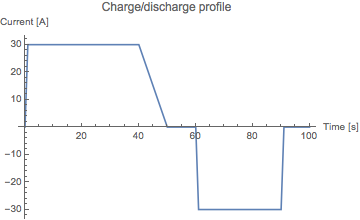
To test out the circuit I connect it to a charger that will charge it with the following profile:
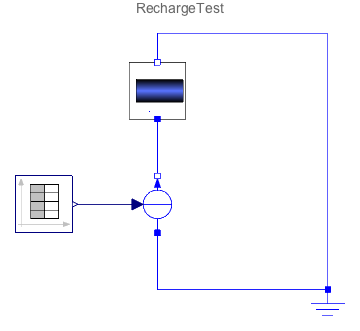
This is the schematic of the supercapacitor along with the charger:
A simulation of the circuit for 100 seconds we can see how the supercapacitor reaches the target 2.7 volt it was designed for after about 40 seconds. It then keeps it's charge for 20 seconds and then starts to discharge from 60 seconds until 90 seconds.
sim1 = WSMSimulate["RechargeTest", {0, 100}];
WSMPlot[sim1, "supercapacitorRechargable.pin_p.v",
PlotLegends -> Placed[{"Battery voltage"}, Below]]
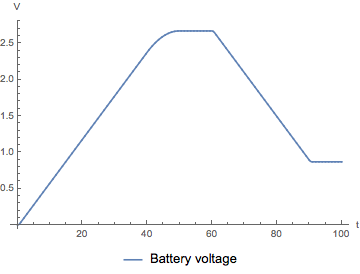
This is a good first circuit: it's easy to model and it simulates very quickly. In many applications this classical equivalent circuit is the right fidelity to capture the dynamics of the supercapacitor. One of the things this circuit is lacking is way to model the short-time transients in the charge and discharge behavior.
To capture the short-time transients we can add another branch in parallel with the main branch. We can also add a voltage dependence to the capacitor, since the behavior changes with the voltage level.
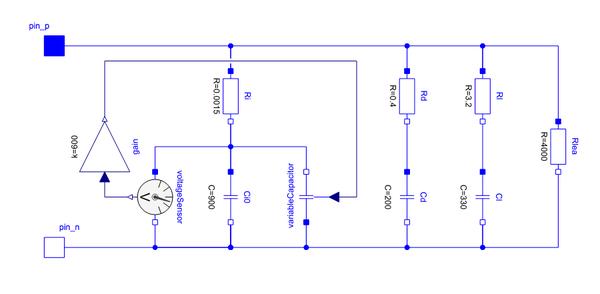
This model is from the paper "Characterization of double-layer capacitors for power electronics applications" by Zubieta and Bonert. It is sometimes called the "Toronto model".
Again I connect it to a current source to charge and discharge it:
sim2 = WSMSimulate["Supercapacitors.Examples.ZubietaDischargeTest470"];
WSMPlot[sim2, {"supercapacitor.pin_p.v"}, {0, 140},
PlotLegends -> Placed[{"Battery voltage"}, Below]]
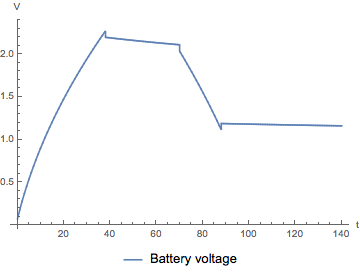
We can now see both the long term behavior (like in the first simulation), and the and short-time transients. The trade-off is that this model has higher complexity, and slightly lower simulation performance, with more circuit elements. More elements also means that more parameters need to be fitted in order to get a behavior that matches the real component.
One can of course go even further and add more branches, more components and get a higher fidelity model. The illustration below shows a summary of different models:
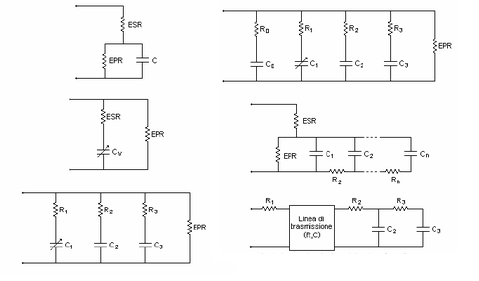
The models used in the post are available as an attachment. Give them a try, and let me know what you create!
References
- Faranda, R.; Gallina, M.; Son, D.T.; A new simplified model of Double-Layer Capacitors 2007; ICCEP '07. International Conference on Clean Electrical Power 21-23 May 2007 Pages:706-710
- Zubieta, L.; Bonert, Richard, "Characterization of double-layer capacitors for power electronics applications," in Industry Applications, IEEE Transactions on , vol.36, no.1, pp.199-205, Jan/Feb 2000
 Attachments:
Attachments: