Awhile ago I showed a Unit Distance Heawood Graph. Here is the McGee graph as a unit-distance graph.
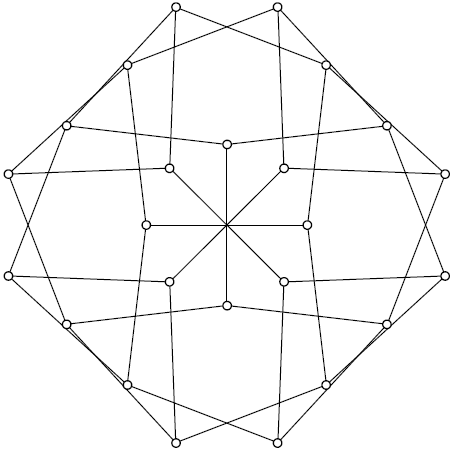
Here's some gory looking code for the points:
McGeePoints =RootReduce[{{0,1/2},{0,-1/2},{1/2,0},{-1/2,0},
{Sqrt[2]/4,Sqrt[2]/4},{-Sqrt[2]/4,Sqrt[2]/4},{Sqrt[2]/4,-Sqrt[2]/4},{-Sqrt[2]/4,-Sqrt[2]/4},
{Cos[a],1/2+Sin[a]},{-Cos[a],1/2+Sin[a]},{Cos[a],-1/2-Sin[a]},{-Cos[a],-1/2-Sin[a]},
{1/2+Sin[a],Cos[a]},{-1/2-Sin[a],Cos[a]},{1/2+Sin[a],-Cos[a]},{-1/2-Sin[a],-Cos[a]},
{Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7],Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8]},
{-Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7],Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8]},
{Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7],-Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8]},
{-Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7],-Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8]},
{Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8],
Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7]},
{-Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8],
Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7]},
{Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8],
-Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7]},
{-Root[81-2592 #1+24192 #1^2-81792 #1^3+149760 #1^4-215040 #1^5-1777664 #1^6+11354112 #1^7-23052288 #1^8+15728640 #1^9+6291456 #1^10-12582912 #1^11+4194304 #1^12&,8],
-Root[81+2592 #1+24192 #1^2+81792 #1^3+149760 #1^4+215040 #1^5-1777664 #1^6-11354112 #1^7-23052288 #1^8-15728640 #1^9+6291456 #1^10+12582912 #1^11+4194304 #1^12&,7]}
}/.a->ArcSin[Root[-71+624 #1+192 #1^2-2688 #1^3-1152 #1^4+3072 #1^5+2048 #1^6&,2]]];
The lines:
McGeeLines={{1,2},{1,9},{1,10},{2,11},{2,12},{3,4},{3,13},{3,15},{4,14},{4,16},{5,8},{5,17},{5,21},{6,7},{6,18},{6,22},{7,19},{7,23},{8,20},{8,24},{9,17},{9,23},{10,18},{10,24},{11,19},{11,21},{12,20},{12,22},{13,18},{13,21},{14,17},{14,22},{15,20},{15,23},{16,19},{16,24}};
That these are unit distance lines can be verified:
Select[McGeeLines, RootReduce[EuclideanDistance[McGeePoints[[#[[1]]]], McGeePoints[[#[[2]]]]]] == 1 &]
From the points and lines we can get the graphic.
Graphics[{Line[McGeePoints[[#]]]&/@McGeeLines,Black,Disk[#,.03]&/@McGeePoints, White,Disk[#,.02]&/@McGeePoints}]
To solve this, I started from
GraphData["McGeeGraph", "AllImages"][[1]]
and put an octagon of diameter 1 at the center. Then I added eight points of the form {Cos[a], 1/2 + Sin[a]}, reflected with mirror symmetries.
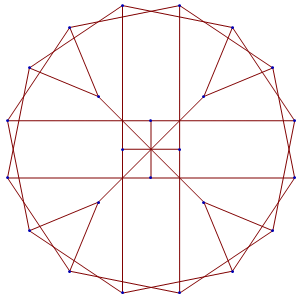
I needed a point at distance 1 from two of the points.
{x, y} /. FullSimplify[Solve[EuclideanDistance[{x, y}, #] == 1 & /@ {{Cos[a], 1/2 + Sin[a]}, {-1/2 - Sin[a], Cos[a]}}, {x, y}]]
The second solution in terms of "a" was the one I wanted. That point needed to be a distance of 1 from {Sqrt[2]/4,Sqrt[2]/4}, so I solved for "a" with NSolve to a thousand digits. RootApproximant didn't recognize it, but did recognize sin(a) as
Root[-71 + 624 #1 + 192 #1^2 - 2688 #1^3 - 1152 #1^4 + 3072 #1^5 + 2048 #1^6 &, 2]
Plugging that into the previous equation gave a pair of order twelve root objects as solutions. Done. More details are in the attached notebook.
 Attachments:
Attachments: