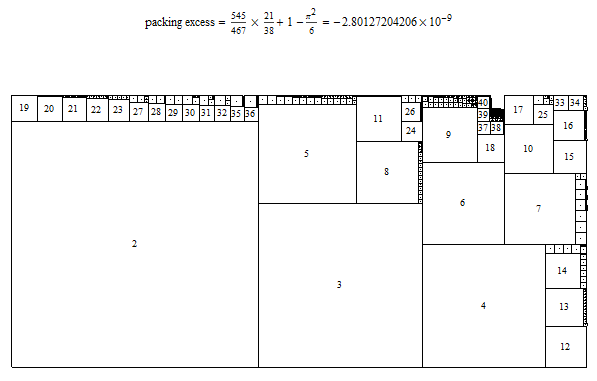
Awhile ago I wrote the Demonstration Packing Squares with Side 1/n. It is based on the Paulhus* method, which starts with a rectangle slightly larger than all the fractional squares, then packs all the squares into it via a clever method.
$$\sum\limits_{a=2}^\infty \frac{1}{a^2} = \frac{\pi^2}{6}-1 \approx 0.644934067 \approx 0.644934069 \approx \frac{545}{467} \times \frac{21}{38}$$
Oblongs of size $ \frac{1}{1} \times \frac{1}{2}$, $ \frac{1}{2} \times \frac{1}{3}$, $ \frac{1}{3} \times \frac{1}{4}$, $ \frac{1}{4} \times \frac{1}{5}$, ... have a total area of 1.
$\sum\limits_{a=1}^\infty \frac{1}{a (a+1)} =1$
I believe it's still an unsolved question whether the infinite rectangles can fit in the unit square. If it's been solved, I'd love to see the paper. Anyways, I haven't figured out how to modify my code to intelligently handle oblongs instead of squares. Can anyone figure that out and use the code to pack the first 2000 oblongs in the unit square?
(*) M. M. Paulhus, "An Algorithm for Packing Squares," Journal of Combinatorial Theory, Series A, 82(2), 1998 pp. 147157.