In this post I will try to explain how I improved my KenKen solver. On an older thread on this forum (here), I pasted my code but without any explanation. Here is an improved version, and with full explanations. The original problem was posted by @Frank Kampas and was about solving the following KenKen:

The goal of the puzzle (as seen above) is to fill the squares with numbers such that the mathematical operators and the solution match for each group of cells (outlines with dark lines). In addition, in each column and in each column you should see the numbers 1 to n, where n is the width/height of grid (this practically means that the numbers in each row or each column are unique). We know that the addition and multiplying are commutative operations. (2+3 = 3+2 and 23 = 32). However this does not hold for subtraction and division (2-3 != 3-2 and 4/2 != 2/4). For these operations the group of cells is considered solved when in one of the two ways the solution is found. i.e. the order of the numbers in the group of cells doesn't matter. I'm using the following indexing for my cells: starting from the top left I have cell 1,1 at the top right cell n,1 and 1,n at the bottom left, and finally 4,4 at the bottom right. So the first coordinate is the x coordinate starting at 1 and pointing to the right. And the y coordinate starts at the top at 1 and points downward.
We start off by defining the KenKen puzzle :
n = 4;
hints = {
{12, Times, {{1, 1}, {2, 1}, {2, 2}}},
{2, Divide, {{3, 1}, {4, 1}}},
{11, Plus, {{1, 2}, {1, 3}, {1, 4}, {2, 3}}},
{2, Minus, {{3, 2}, {3, 3}}},
{2, Plus, {{4, 2}}},
{4, Plus, {{4, 3}, {4, 4}}},
{3, Minus, {{2, 4}, {3, 4}}}
};
Here the syntax is as follows: n gives the size of the box, and for the hints the first parameter is the result of group of cells, the second parameter the operation (multiply, divide, add or subtract), and the last parameter is a list of cells. The basic approach for this solver is as follows: We have an n*n grid of cells. Each cell starts with n candidates (1,2,3...n-1,n). We iteratively cross out candidates until we have only one candidate left per cell. Let's define all the candidates:
cands = ConstantArray[Range[n], {n, n}];
We can visualize it as follows:
Grid[cands, Frame -> All, ItemSize -> {7, 7}]
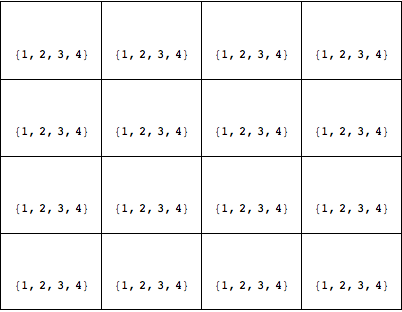
Let's now visualize the playing grid including the hints:
hintstyle=Sequence[11,Red]; (* style for the hints *)
candstyle=Sequence[8,Gray]; (* style for the candidates *)
fixedstyle=Sequence[22,Black]; (* style for the solved numbers *)
linestyle=Sequence[Thickness[0.01],JoinForm["Round"],CapForm["Round"]]; (* styling for the thick lines *)
thinlinestyle=Sequence[GrayLevel[0.85],Thickness[0.005],JoinForm["Round"],CapForm["Round"]]; (* and for thin lines *)
opchars={Plus->"+",Minus->"-",Times->"*",Divide->"/"}; (* symbols for the operators *)
ClearAll[SquareSides,ClueText,DrawGrid]
(* gives 4 edges of a cell *)
SquareSides[n_,m_]:={{{n,-m},{n+1,-m}},{{n,-m},{n,-m-1}},{{n+1,-m},{n+1,-m-1}},{{n,-m-1},{n+1,-m-1}}}
(* gives the text for inside the cell *)
ClueText[cands_,{x_,y_}]:=Module[{center,r=0.2,cp},
center={x+0.5,-y-0.5}; (* center of the cell *)
If[Length[cands]==1, (* if there is 1 candidate then it is fixed *)
Text[Style[First[cands],fixedstyle],center]
,
cp=CirclePoints[center,{r,\[Pi]/2},n]; (* multiple candidates are displayed on a circle from the center *)
cp=MapThread[Text[Style[#1,candstyle],#2]&,{Range[n],cp}][[cands]];
cp
]
]
DrawGrid[cands_List,hints_List]:=Module[{hor,ver,all,rem,boxborders,topleft,hinttext,candpos,candtext},
hor=Flatten[Outer[List,Range[n],Range[n+1]],1]; (* horizontal lines *)
ver=Flatten[Outer[List,Range[n+1],Range[n]],1]; (* vertical lines *)
all=Join[{#,#+{1,0}}&/@hor,{#,#+{0,1}}&/@ver]; (* all lines *)
all[[All,All,2]]*=-1; (* coordinates are flipped upside-down *)
topleft=First[TakeSmallestBy[#,Total,1]]&/@hints[[All,3]]; (* find the top-left of each group of cells*)
topleft+=0.08; (* offset the coordinate a little bit*)
topleft[[All,2]]*=-1; (* also flip upside down*)
hinttext=ToString[#1]<>(#2/.opchars)&@@@hints; (* find he symbol for the operation *)
hinttext=MapThread[Text[Style[#1,hintstyle],#2,{-1,1}]&,{hinttext,topleft}]; (* make the hint-texts *)
boxborders=Apply[SquareSides,hints[[All,3]],{2}]; (* for each group of cells find all the 4 sides for all the cells *)
boxborders=Flatten[#,1]&/@boxborders; (* flatten the sides so each group of cells now has n*4 borders*)
boxborders=Select[Tally[#],Last[#]==1&][[All,1]]&/@boxborders; (* if a border appears twice it means it is shared, we only want borders that appear once *)
boxborders=Flatten[boxborders,1]; (* flatten again to keep the border of all the cells *)
rem=Complement[all,boxborders]; (* this are all the 'inner' borders *)
candpos=Tuples[Range[n],2]; (* position for the candidates *)
candtext=MapThread[ClueText,{Flatten[cands,1],candpos}]; (* clue texts for each cell *)
Graphics[{{thinlinestyle,Line/@rem}, (* assemble everything*)
hinttext,
{linestyle,Line[boxborders]},
candtext
},ImageSize->65n]
]
Let's try the visualization out with our unsolved KenKen puzzle:
DrawGrid[cands, hints]

looks great! The gray small numbers are the candidates, the big ones are solved. In red the solution and the operator. Now let's get into the solving the puzzle! Let's look at the bottom-right cell. Cell 4,3 and cell 4,4 should add up to 4. So let's look at the possibilities:
TableForm[Table[Style[i+j,If[i+j==4,Red,Black]],{i,4},{j,4}],TableHeadings->{"4,3 = "<>ToString[#]&/@Range[4],Column[{"4,4","=",#},Center]&/@Range[4]}]

there are only 3 possibilities (marked in red): {1,3} {2,2} {3,1} What we observe, is that 4 is not one of the candidates, we can therefore eliminate the candidate 4 from cells 4,3 and 4,4. Similarly we can look at the top-right group of cells, the quotient of the two numbers should be 2.
TableForm[Table[Style[Exp@Abs@Log[i/j],If[Abs@Log[i/j]==Log[2],Red,Black]],{i,4},{j,4}],TableHeadings->{"3,1 = "<>ToString[#]&/@Range[4],Column[{"4,1","=",#},Center]&/@Range[4]}]
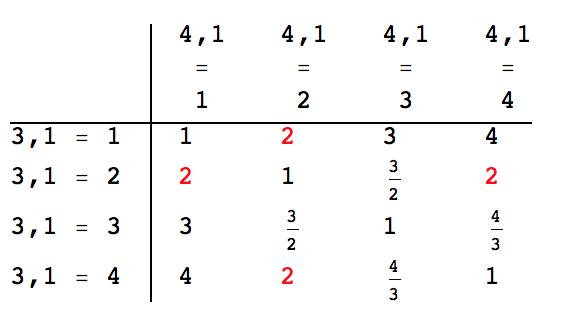
So the possibilities (marked again in red) are: {1,2} {2,1} {2,4} {4,2} Here we see that 3 is not a candidate, and 3 can therefore be removed as candidate from cells 4,1 and 3,1.
For a group of 3 or more cells, this becomes more and more complicated. and visualing it become tricky on 2D screens. But one can imagine trying all the combination of all candidates of cell 1,1 and 2,1 and 2,2 and check for those for which the product is 120:
Select[Tuples[Range[4], 3], Times @@ # == 12 &]
{{1, 3, 4}, {1, 4, 3}, {2, 2, 3}, {2, 3, 2}, {3, 1, 4}, {3, 2, 2}, {3,4, 1}, {4, 1, 3}, {4, 3, 1}}
you will find the above possibilities. Unfortunately we can not exclude any candidate because 1,2, 3, and 4 all show up in all cells. In order to solve the puzzle we iteratively check if we can cross out candidates until we can't go any further:
for each group of cells (each hint)
[
get the possible candidates for those cells.
compute the outcome for each possible set of candidates using the operator of the hint
filter those possible set of candidates for which the outcome is the right one
check the possible candidates for each cell and put those back
]
So here is the code:
ClearAll[ConvertHint,ApplyHint]
ConvertHint[ans_,Divide,cells_]:={Log[ans],Abs[Log[#1/#2]]&,cells} (* this is how we deal with division *)
ConvertHint[ans_,Minus,cells_]:={Abs[ans],Abs[#1-#2]&,cells} (* this is how we deal with subtraction *)
ConvertHint[ans_,op_,cells_]:={ans,op,cells} (* plus and times stay the same *)
ApplyHint[ans_Integer,op_,cells_List]:=ApplyHint[ConvertHint[ans,op, cells]] (* we convert the hint in order to account for subtraction and division*)
ApplyHint[{ans_,op_,cells_List}]:=Module[{cns},
cns=Extract[cands,cells]; (* get candidates from each cell *)
cns=Select[Tuples[cns],op@@#==ans&]; (* find all the possibilities for those candidates and filter those for which the operator results in the answer*)
cns=Union/@(cns\[Transpose]); (* look at the unqiue andidates left for those good solutions *)
MapThread[(Part[cands,Sequence@@#2]=#1)&,{cns,cells}] (* put those (filtered) candidates back *)
]
let's run it once and check each hint:
ApplyHint @@@ hints;
let's visualize the grid:
DrawGrid[cands, hints]

ok pretty good! We lost the 3 from the top-right cells, and the 4 from the bottom-left cells. As well as 2 and 3 from the mid-bottom cells. And the 'group' of cells at 4,2 is now solved. We can however, retry the elimination process and see what happens:
ApplyHint@@@hints;
DrawGrid[cands,hints]

unfortunately nothing happens for this particular puzzle. So we have to come up with something smarter. We can be smarter in our ApplyHint function. We try out all the possible candidates for each cells, and try to combine them. We pick those out for which the operation yields the correct result, but it does not necessarily mean it is a valid combination, as we also need that for each row and for each column the numbers are unique. So we can also filter those out while checking. We modify our script:
for each group of cells (each hint)
[
get the possible candidates for those cells.
compute the outcome for each possible set of candidates using the operator of the hint
**filter those possible sets of candidates for which the outcome is the right one**
filter those possible sets of candidates for which it is violation of the unique row/column rule
check the possible candidates for each cell and put those back
]
Here is the code:
ClearAll[ConvertHint,CandAssassin,CandAssassinHelper,ApplyHint]
ConvertHint[ans_,Divide,cells_]:={Log[ans],Abs[Log[#1/#2]]&,cells}
ConvertHint[ans_,Minus,cells_]:={ans,Abs[#1-#2]&,cells}
ConvertHint[ans_,op_,cells_]:={ans,op,cells}
ApplyHint[ans_Integer,op_,cells_List]:=ApplyHint[ConvertHint[ans,op, cells]]
ApplyHint[{ans_,op_,cells_List}]:=Module[{cns},
cns=Extract[cands,cells];
cns=Select[Tuples[cns],op@@#==ans&];
cns=CandAssassin[cns,cells]; (* this is the new line and check if solutions respect to unique row/column rule *)
cns=Union/@(cns\[Transpose]);
MapThread[(Part[cands,Sequence@@#2]=#1)&,{cns,cells}]
]
CandAssassinHelper[cn_List,icell_List]:=AllTrue[icell,Unequal@@cn[[#]]&]
CandAssassin[cns_List,cells_List]:=Module[{icell,newcans},
icell={Range[Length[cells]],cells}\[Transpose]; (* number each cell (index) *)
icell=GatherBy[icell,#[[2,1]]&][[All,All,1]]; (* gather by the 'x' coordinate of the cells, return the indices of the cells*)
newcans=Select[cns,CandAssassinHelper[#,icell]&]; (* filter out those candidates for which the candidates in cells with same 'x' coordinates are the same*)
icell={Range[Length[cells]],cells}\[Transpose]; (* now the same but in the vertical direction*)
icell=GatherBy[icell,#[[2,2]]&][[All,All,1]];
Select[newcans,CandAssassinHelper[#,icell]&]
]
We use two helper functions in order to filter out those combinations.
ApplyHint @@@ hints;
DrawGrid[cands, hints]

We apply the function and see that we eliminated the 1 from 2,3 and the 2 from 2,1. Not bad. But we can add more smarts to our solver.
We know that each row and column should be unique. We can already see that cell 4,2 is 'solved'. That means that in the second row, and the forth column we should not have any other 2. So we can eliminate candidate 2 from cells 1,2 2,2 3,2 4,1 4,3 and 4,4.
Similarly we can look at cells 2,4 and 3,4 at the bottom: they both have candidates 1 and 3. This means the solution is either {1,3} or {3,1}. Which basically means that in the other two cells in that row we can not have a 1 nor a 3! Because that would violate the unique row rule!
We can generalize the above statement into a 'theorem': for m cells within a row/column with a total of m distinct candidates, we can eliminate those m candidates from the other n-m cells in that row/column. This 'theorem' is widely used in Sudoku where it is called a 'naked subset'. I will use the same terminology here.
ClearAll[DeleteCands,NakedSubset,NakedSubsetCheck,NakedDelete]
DeleteCands[{n_,m_},del_]:=(Part[cands,n,m]=Complement[Part[cands,n,m],del])
NakedDelete[cells_List,samesubs_List]:=Module[{other,digits},
other=Complement[cells,samesubs]; (* cells to delete from *)
digits=First[Extract[cands,samesubs[[{1}]]]]; (* what to delete *)
Do[DeleteCands[o,digits],{o,other}] (* delete them one-by-one *)
]
NakedSubsetCheck[cells_List]:=Module[{celldata,n=Length[cells]},
celldata=Extract[cands,cells]; (* extract candidates from cells *)
If[AllTrue[celldata,Length[#]<=n&], (* number of candidates should be smaller or equal to the number of cells *)
Length[Union@@celldata]==n (* n cells with n different numbers*)
,
False
]
]
NakedSubset[m_Integer]:=Module[{cellgroups},
cellgroups=Join[Outer[List,Range[n],Range[n]],Outer[List,Range[n],Range[n]]\[Transpose]]; (* all rows and all columns *)
Do[NakedSubset[m,cg],{cg,cellgroups}] (* for each row/column try out the naked subsets of size m *)
]
NakedSubset[m_Integer,cells_List]:=Module[{subsets},
subsets=Subsets[cells,{m}]; (* all the subsets of cells with size m *)
subsets=Select[subsets,NakedSubsetCheck]; (* select those for which hold that we have n cells with n numbers *)
Do[NakedDelete[cells,ss],{ss,subsets}] (* delete from the other cells *)
]
Let's first try Naked Subsets of size 1:
NakedSubset[1];
DrawGrid[cands, hints]

We have eliminated the 2 from row 2, and from column 4. Now let's do the Naked Subset for size 2:
NakedSubset[2];
DrawGrid[cands, hints]

This has eliminated 1 and 4 from the bottom left and bottom right cell, and has only left 3 in the bottom right, so that is solved. Let's do it a few times:
Do[
NakedSubset[1];
NakedSubset[2];
,
{10}
]
DrawGrid[cands, hints]
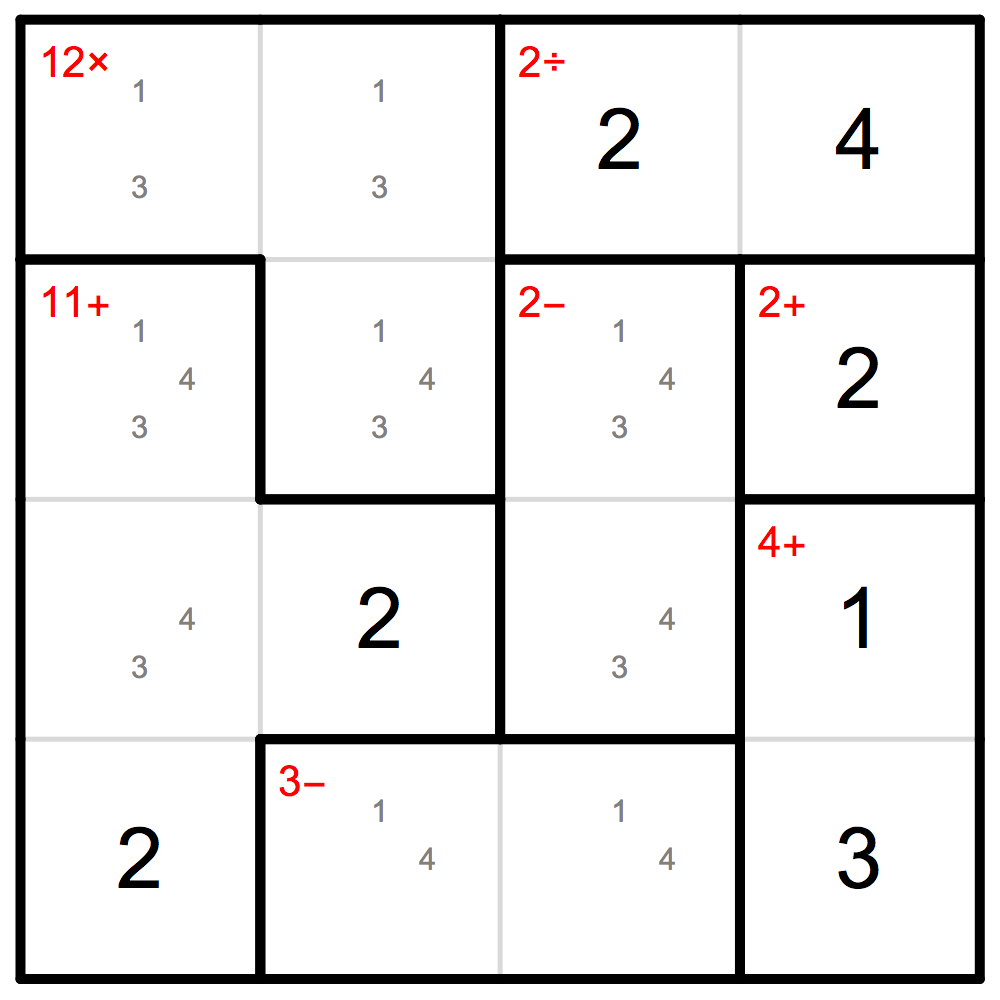
Now we can continue with higher sizes for the naked subset:
Do[
NakedSubset /@ Range[n];
,
{10}
]
DrawGrid[cands, hints]
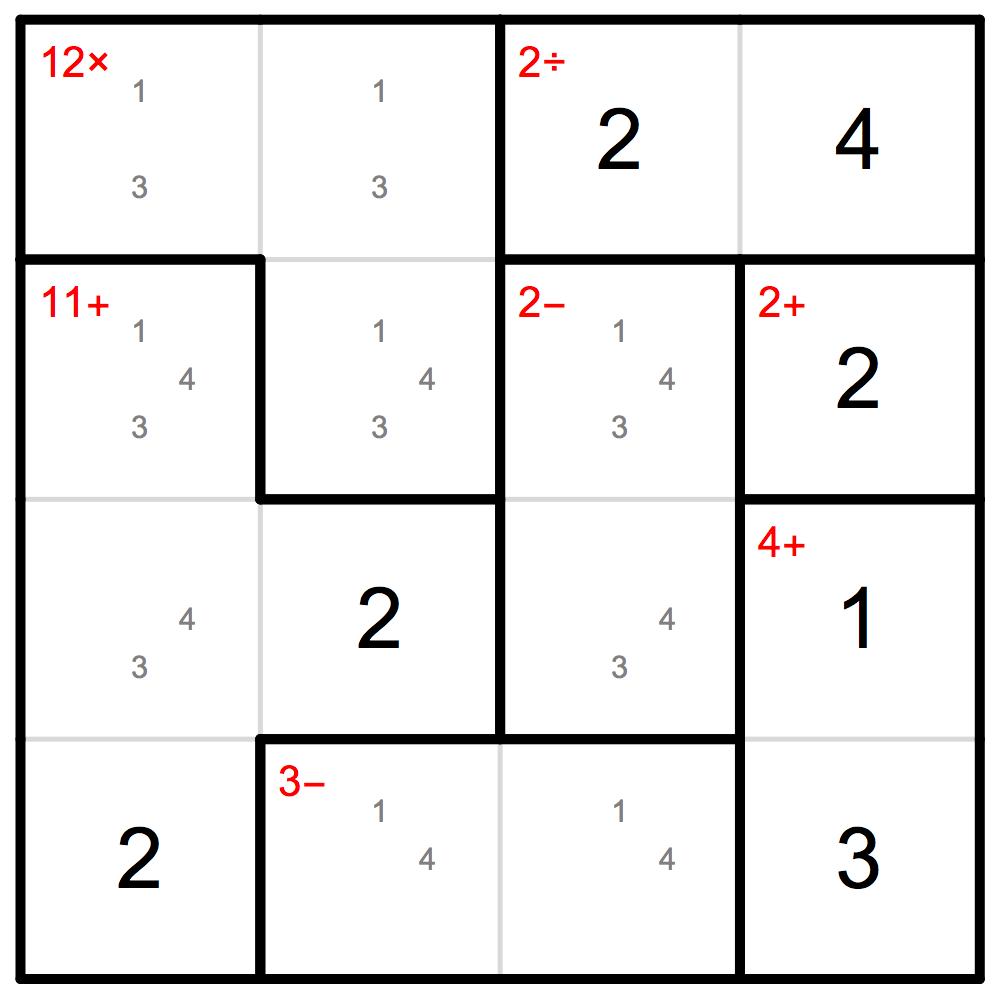
However this does not solve it just yet...Perhaps we can try to apply our hints again:
ApplyHint @@@ hints;
DrawGrid[cands, hints]
Do[
NakedSubset /@ Range[n];
,
{10}
]
DrawGrid[cands, hints]
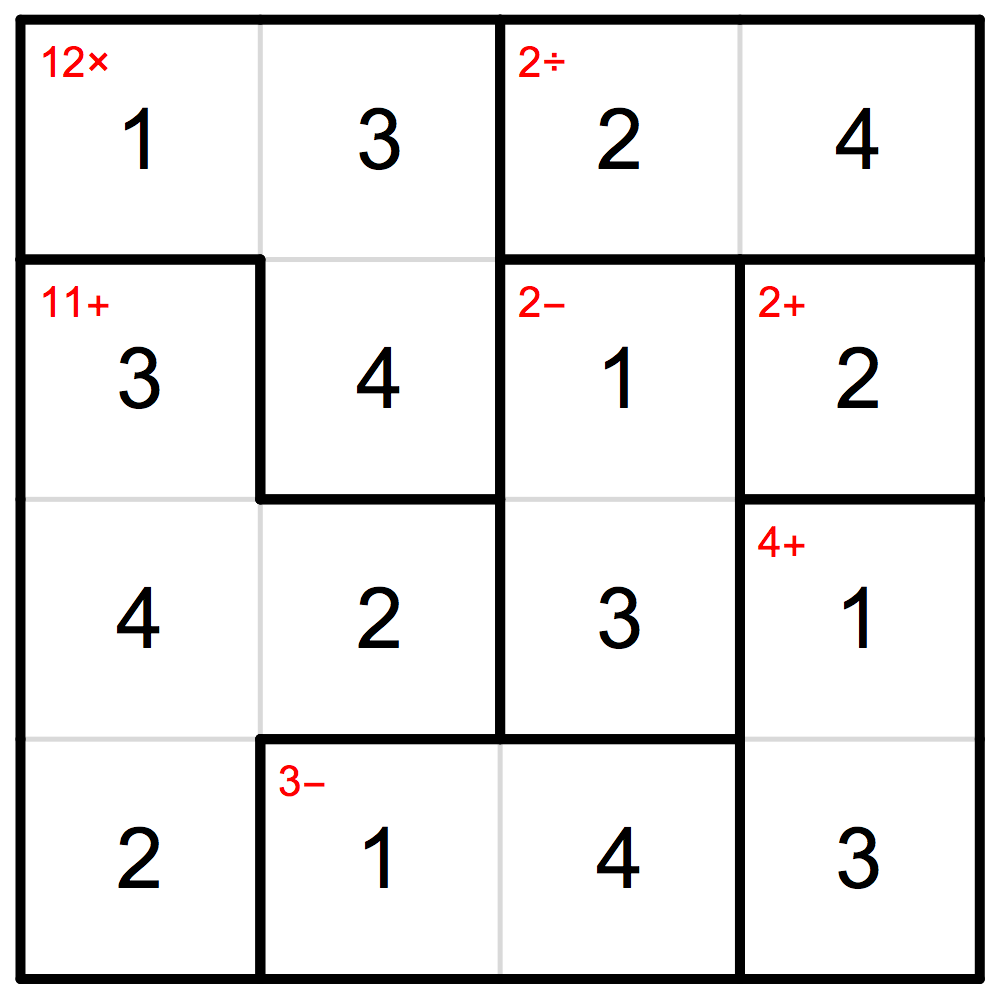
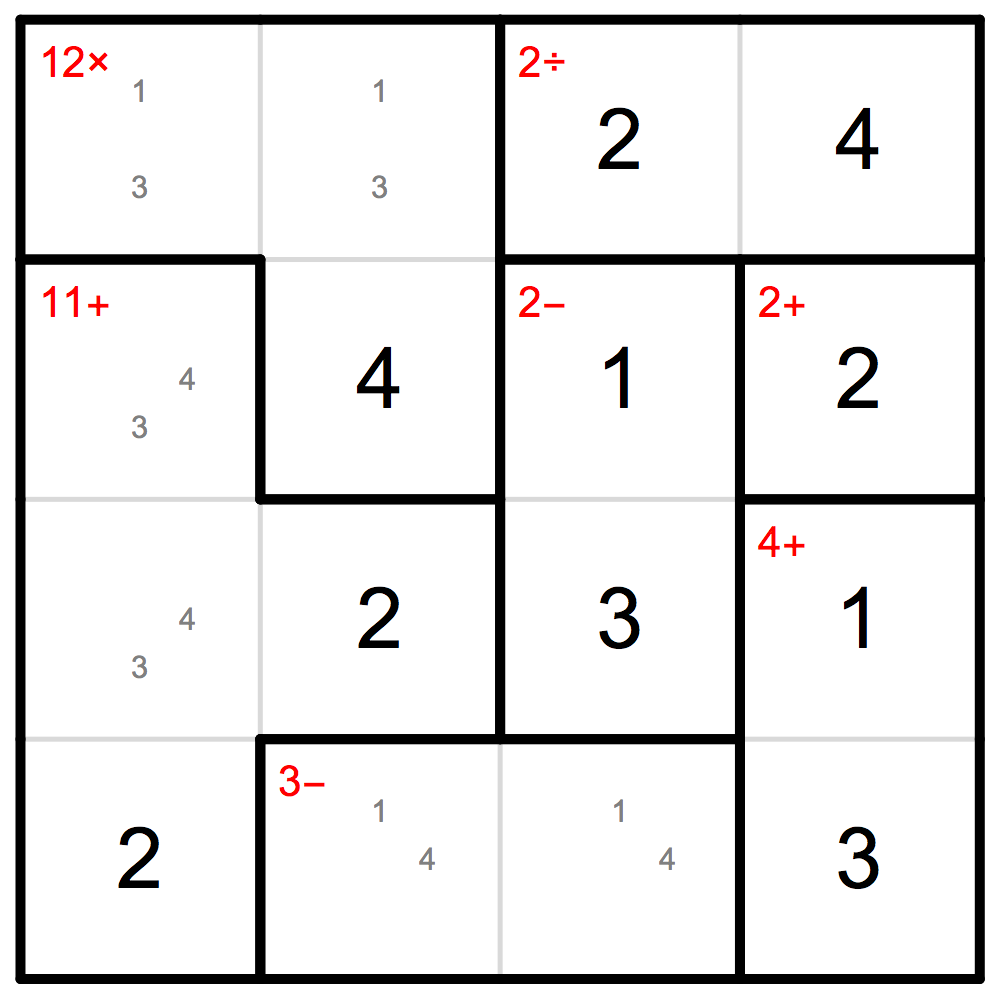
And we solved the problem! Lets make a function who does it automatically:
AbsoluteTiming[
cands=ConstantArray[Range[n],{n,n}];
old=False;
While[old=!=cands,
old=cands;
ApplyHint@@@hints;
If[old===cands,
NakedSubset/@Range[n];
];
];
]
DrawGrid[cands,hints]
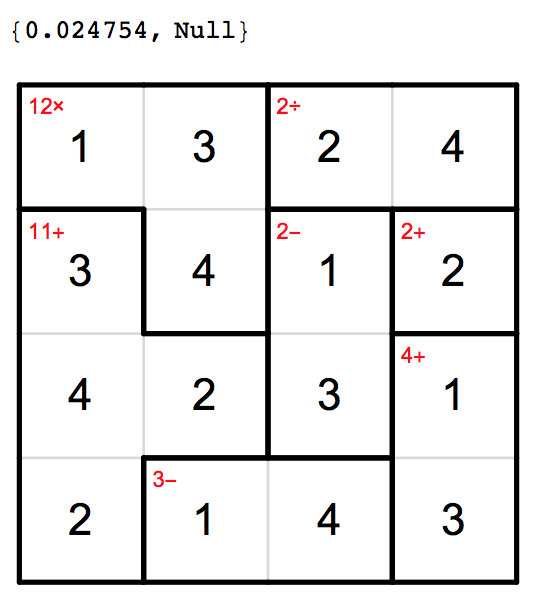
25 milliseconds; pretty good but what about more difficult problems? Here is a puzzle from http://www.kenkenpuzzle.com/howto/hard . Let's try:
n=6;
hints={{13,Plus,{{1,1},{1,2},{2,1},{2,2}}},{180,Times,{{3,1},{4,1},{5,1},{4,2}}},{9,Plus,{{6,1},{6,2},{6,3}}},{2,Plus,{{3,2}}},{20,Times,{{5,2},{5,3}}},{15,Plus,{{1,3},{1,4},{1,5}}},{6,Times,{{2,3},{3,3}}},{11,Plus,{{4,3},{4,4},{3,4}}},{3,Plus,{{2,4}}},{9,Plus,{{5,4},{6,4},{5,5},{4,5}}},{2,Divide,{{2,5},{3,5}}},{8,Plus,{{1,6},{2,6},{3,6}}},{18,Plus,{{4,6},{5,6},{6,6},{6,5}}}};
AbsoluteTiming[
cands=ConstantArray[Range[n],{n,n}];
old=False;
While[old=!=cands\[And]\[CurlyPhi]<100,
old=cands;
ApplyHint@@@hints;
If[old===cands,
NakedSubset/@Range[n];
];
];
]
DrawGrid[cands,hints]
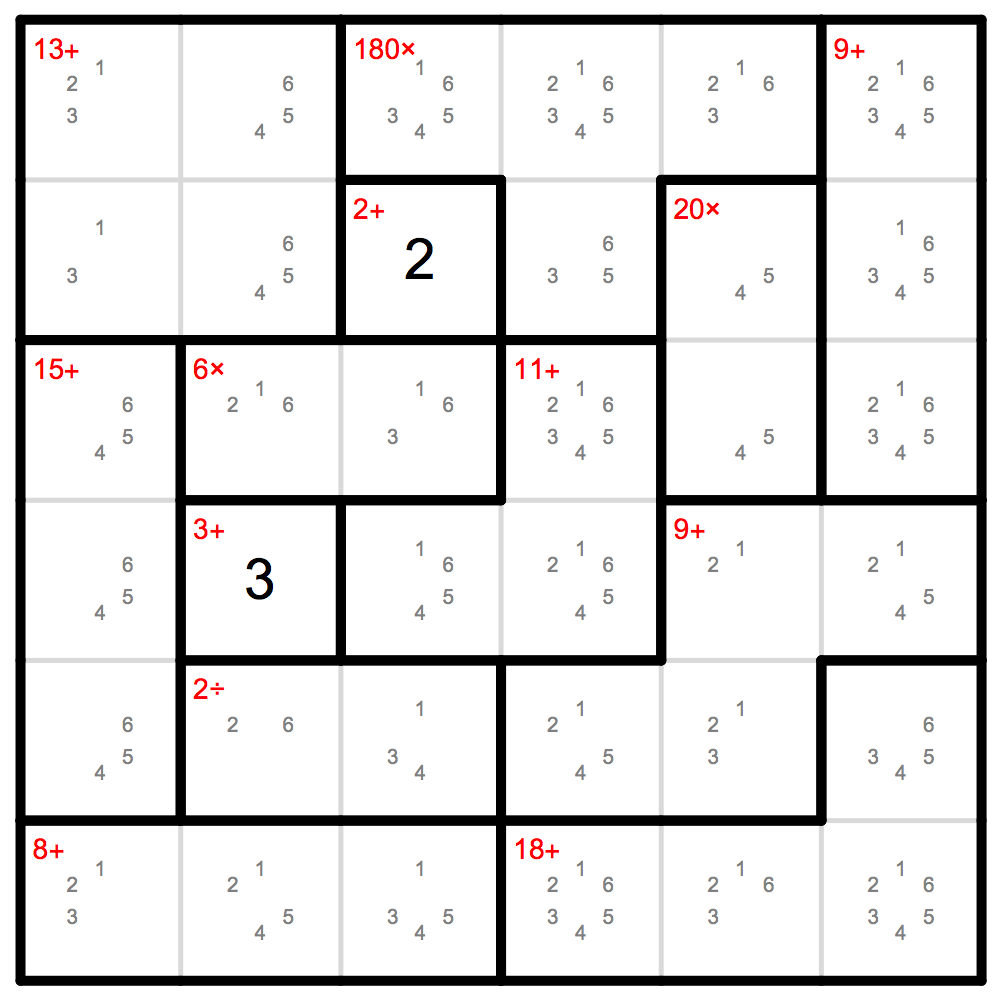
The algorithm does it work and eliminates 60 candidates (n^3-Length[Flatten[cands]]) which solved 2 numbers in the grid. We have to come up with something smarter in order to solve this one! Let's look at pairs of hints and check if we can try all possibilities simultaneously (again I borrow the naming from Sudoku solving):
ClearAll[BoxBoxInteraction]
BoxBoxInteraction[]:=BoxBoxInteraction/@Apply[ConvertHint,Subsets[hints,{2}],{2}] (* get every pair of two hints and conver the hints *)
BoxBoxInteraction[hints_List]:=Module[{ans,ops,cellss,cns},
{ans,ops,cellss}=Transpose[hints]; (* get the two hints and transpose them *)
cns=Extract[cands,#]&/@cellss; (* retrieve the candidates of two sets of cells *)
cns=Tuples/@cns; (* for each of them enumerate all possibilities *)
cns=Table[Select[cns[[\[Iota]]],ops[[\[Iota]]]@@#==ans[[\[Iota]]]&],{\[Iota],Length[hints]}]; (* filterout those that matches the hint for each hint *)
cns=MapThread[CandAssassin,{cns,cellss}]; (* check for row/column uniqueness for each hint *)
cns=Tuples[cns]; (* combine the solutions for each hint *)
cns=Flatten[cns,{{1},{2,3}}]; (* transpose and flip it around and *magic* *)
cellss=Flatten[cellss,1]; (* put all the cells on a big pile *)
cns=CandAssassin[cns,cellss]; (*check row/column uniqueness *)
cns=Union/@Transpose[cns]; (* filter unique candidates for each cells *)
MapThread[(Part[cands,Sequence@@#2]=#1)&,{cns,cellss}]; (* put those back in the cell *)
]
Let's try it out:
n=6;
AbsoluteTiming[
cands=ConstantArray[Range[n],{n,n}];
old=False;
While[old=!=cands,
old=cands;
AbsoluteTiming[ApplyHint@@@hints;];
NakedSubset/@Range[n];
If[old==cands,
BoxBoxInteraction[];
];
];
]
DrawGrid[cands,hints]
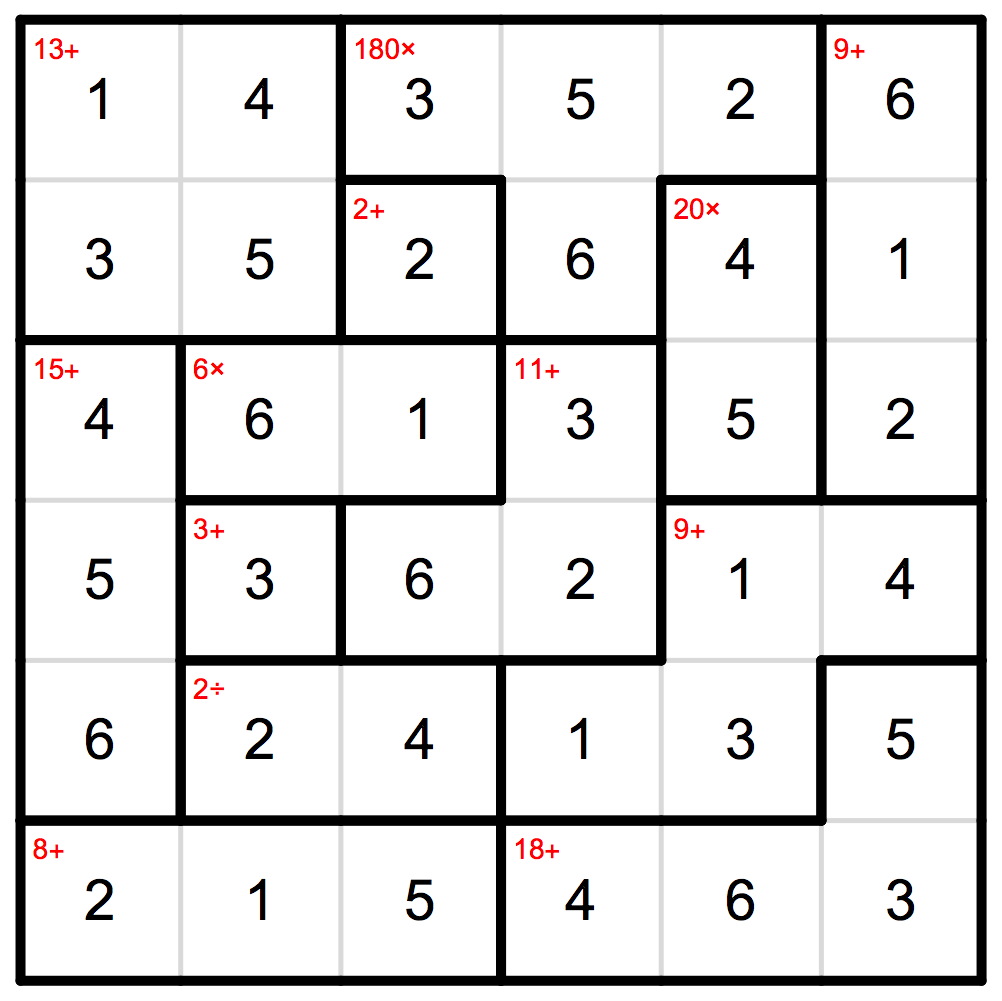
That solved also this puzzle! I have yet to find a puzzle that was not solved using this methods. In addition one can expand the BoxBoxInteraction to look at triplets and quadruplets of ultimate all hints simultaneously; though very costly in memory it is guaranteed to find the solution (if it is unique).
I hope that this post will not only help you solve your KenKen puzzles but also taught you the solving technique. This technique is widely used in Sudoku solvers as well, and can be extended to other types of puzzles as well.
Lastly, I'd like to thank Frank again for asking the original question!