Message Boards Message Boards

0
|
7519 Views
|
13 Replies
|
4 Total Likes
View groups...
Share
Share this post:

Finding the inverse of a mapping of a disk onto an airfoil

SALIOU TELLY
Posted 9 years ago

Good day all!

I am somewhat new to mathematica and has been working on trying to find the inverse map to a mapping that I have analytically formulated (Note that the formulation was first done in the complex domain before being expressed in the cartesian form). The formulated cartesian equations below map a 2-D annulus to an annular airfoil as shown in the figures.

$$\text{xa} = \frac{1}{2} \left(\frac{\lambda ^2 \left(\text{xd}^2+\text{yd}^2\right) \left(\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)}{\left(\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)^2+\left(\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)^2}+\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)$$

$$\text{ya} = \frac{1}{2} \left(-\frac{\lambda ^2 \left(\text{xd}^2+\text{yd}^2\right) \left(\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)}{\left(\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)^2+\left(\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)^2}+\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)$$

Here ( $\text{xa}$,$\text{ya} $) are coordinates of points on the airfoil annulus, which are mapped points from ($\text{xd} $,$\text{yd} $) on the circular annulus. Everything else are just constant parameters; in the figures shown $\rho = 2$; $\alpha = -.25$; $\beta = 0$; $\lambda = 1.75$; and the circular annulus has outer diameter of 2 units and inner diameter of 1 unit.

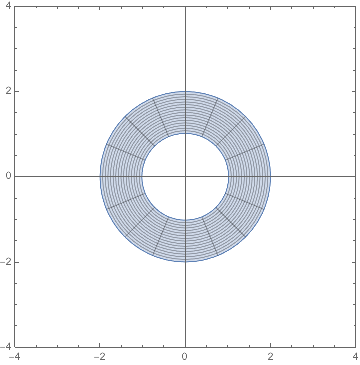
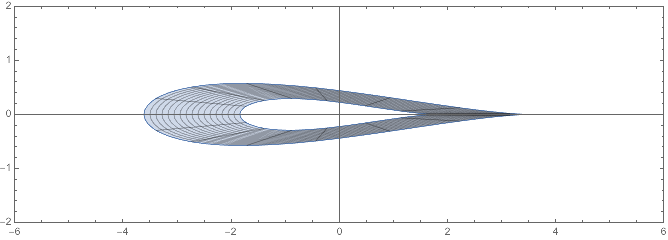
Circular annulus before mappingMapped airfoil annulus

Now, I am interested in finding the inverse map. In other words, I would like to express ( $\text{xd}$,$\text{yd} $) as function of ($\text{xa} $,$\text{ya}$), if possible.

I have not been successful in doing so analytically, and I was hoping that with mathematica I would be able to symbolically solve for the inverse map with "Solve". However, "Solve" has not provided any output (may be because of computational limitation).

Is there any reason why this inverse map will not exist?
I am fairly familiar with the inverse function theorem and thought the inverse would exist at most points despite the cusp at the trailing edge.

If the inverse map exists, am I limited by the computational power of my machine or is there any other approach that can help?

Any assistance in the right direction will be greatly appreciated...

Saliou Telly
POSTED BY: SALIOU TELLY
13 Replies
Sort By:

I wonder if you can interpolate the derivatives, instead of derivating the interpolation.
POSTED BY: Gianluca Gorni

If a numerical inverse is enough for you, you can compute the direct transformation in the points in a grid, reverse the order and then use something like ListInterpolation.
POSTED BY: Gianluca Gorni
SALIOU TELLY
SALIOU TELLY
Posted 9 years ago

Thanks Gianluca for the suggestion!

I was trying to first take the route of finding an expression for the inverse, but I may have to look at the numerical inverse or just formulate a transformation from scratch to map interior points of an airfoil onto interior points of a circle.

The issue with the numerical inverse is that I plan to next find the deformation gradient matrix and its Jacobian from this map, which involves finding derivatives with respect to variables. That task would be "easier" if I could find an explicit expression ....

Thanks again,

Saliou
POSTED BY: SALIOU TELLY
SALIOU TELLY
SALIOU TELLY
Posted 9 years ago

Daniel,

Thanks for the suggestion.

Attached is the simplified notebook that I am using....

Regards,

Saliou Telly

Attachments:
POSTED BY: SALIOU TELLY

I made a few small modifications. I did not check which, if any, make a difference to the outcome.

(1) I made all numbers exact. This could be an issue, for example, in "symbolic" handling of square roots.

(2) I converted the equations to expressions.

(3) I did not define x and y to be functions of r and theta. I expect that this makes the reverse solving problem easier. In particular we can now solve for those rather than for the {r,theta} pair.

Ro = 2;
Ri = 1;
\[Rho] = 2;
\[Alpha] = -1/4;
\[Beta] = 0;
\[Lambda] = 7/4;

exprs = {-xd + (Ri*x)/(x^2 + y^2)^(1/2) + ((Ro - Ri)/Ro)*x, 
      -yd + (Ri*y)/(x^2 + y^2)^(1/2) + ((Ro - Ri)/Ro)*y};

Timing[solns = Simplify[Solve[exprs == 0, {x, y}]]]

(* Out[156]= {0.546003, {{x -> (
    2 (xd^3 + xd yd^2 - Sqrt[xd^2 (xd^2 + yd^2)]))/(xd^2 + yd^2), 
   y -> (2 yd (xd^3 + xd yd^2 - Sqrt[xd^2 (xd^2 + yd^2)]))/(
    xd (xd^2 + yd^2))}, {x -> (
    2 (xd^3 + xd yd^2 + Sqrt[xd^2 (xd^2 + yd^2)]))/(xd^2 + yd^2), 
   y -> (2 yd (xd^3 + xd yd^2 + Sqrt[xd^2 (xd^2 + yd^2)]))/(
    xd (xd^2 + yd^2))}}} *)

It might be overwhelming in terms of complexity to do a full symbolic solution of the original pair of equations. Specializing the parameters makes it viable. So you might want to consider having a function that just inverts when given specific values of those parameters.
POSTED BY: Daniel Lichtblau
SALIOU TELLY
SALIOU TELLY
Posted 9 years ago

Thanks Daniel!

I am actually interested in the inverse of the last map in the notebook ((xd, yd) ---> (xa, ya)), which maps the circular annulus to the airfoil annulus. So I would like to find an expression for the inverse map ((xa, ya) ---> (xd, yd)).

What you have solved is the inverse mapping of a circular disk to a circular annulus, which was just a step that I use to generate a circular annulus before mapping it to an airfoil annulus.

I will try your approach to see if it helps in finding the inverse map of interest.....

Thanks again,

Saliou
POSTED BY: SALIOU TELLY

I doubt it will give a usable result. I transformed to polar because that made the expressions more tractable; this involves also making new variables for sine and cosine, and adding the usual identity to link those algebraically. Found there are four solutions and they are huge. For better control over the process I used GroebnerBasis directly, then used Roots to solve for the radial variable, and back-substituted to get the sine and cosine solution for the angular variable (there is one per radial solution).

e1 = {- xa + 
    1/2*(\[Rho]*xd + \[Alpha]* 
        Sqrt[(xd^2) + (
         yd^2) ] + (\[Lambda]^2*(xd^2 + 
          yd^2)*(\[Rho]*xd + \[Alpha]*  
           Sqrt[(xd^2) + (yd^2) ]))/((\[Rho]* xd + \[Alpha]*  
           Sqrt[(xd^2) + (yd^2) ])^2 + (\[Rho]* yd + \[Beta]* 
           Sqrt[(xd^2) + (yd^2) ])^2)),
   -ya + 1/
     2*(\[Rho]*yd + \[Beta]* 
        Sqrt[(xd^2) + (
         yd^2) ] - (\[Lambda]^2*(xd^2 + 
          yd^2)*(\[Rho]*yd + \[Beta]*  
           Sqrt[(xd^2) + (yd^2) ]))/((\[Rho]* xd + \[Alpha]*  
           Sqrt[(xd^2) + (yd^2) ])^2 + (\[Rho]* yd + \[Beta]* 
           Sqrt[(xd^2) + (yd^2) ])^2))};
e2 = e1 /. {(xd^2 + yd^2) -> r^2, Sqrt[(xd^2) + (yd^2) ] -> r};

e3 = Join[
   Together[
    e2 /. {xd -> r*ctheta, yd -> r*stheta}], {ctheta^2 + stheta^2 - 
     1}];

Timing[gb = 
   GroebnerBasis[e3, {ctheta, stheta, r}, 
    CoefficientDomain -> RationalFunctions];]

(* Out[57]= {2.448772, Null} *)

radii = Solve[gb[[1]] == 0, r, Quartics -> False];
gb2 = Rest[gb] /. radii[[1]];

sin = Solve[gb2[[1]] == 0, stheta];
cos = Solve[gb2[[2]] == 0, ctheta];

As I wrote, this is probably too large to be useful. And there are three others; which is "correct" could vary with parameter values, including the specific values of xa and ya.

In[82]:= radii[[1]]

(* Out[82]= {r -> 
  Root[16 xa^4 \[Alpha]^4 + 32 xa^2 ya^2 \[Alpha]^4 + 
     16 ya^4 \[Alpha]^4 + 32 xa^4 \[Alpha]^2 \[Beta]^2 + 
     64 xa^2 ya^2 \[Alpha]^2 \[Beta]^2 + 
     32 ya^4 \[Alpha]^2 \[Beta]^2 + 16 xa^4 \[Beta]^4 + 
     32 xa^2 ya^2 \[Beta]^4 + 16 ya^4 \[Beta]^4 - 
     16 xa^4 \[Alpha]^2 \[Rho]^2 - 32 xa^2 ya^2 \[Alpha]^2 \[Rho]^2 - 
     16 ya^4 \[Alpha]^2 \[Rho]^2 - 16 xa^4 \[Beta]^2 \[Rho]^2 - 
     32 xa^2 ya^2 \[Beta]^2 \[Rho]^2 - 
     16 ya^4 \[Beta]^2 \[Rho]^2 + (-32 xa^3 \[Alpha]^5 - 
        32 xa ya^2 \[Alpha]^5 - 32 xa^2 ya \[Alpha]^4 \[Beta] - 
        32 ya^3 \[Alpha]^4 \[Beta] - 64 xa^3 \[Alpha]^3 \[Beta]^2 - 
        64 xa ya^2 \[Alpha]^3 \[Beta]^2 - 
        64 xa^2 ya \[Alpha]^2 \[Beta]^3 - 
        64 ya^3 \[Alpha]^2 \[Beta]^3 - 32 xa^3 \[Alpha] \[Beta]^4 - 
        32 xa ya^2 \[Alpha] \[Beta]^4 - 32 xa^2 ya \[Beta]^5 - 
        32 ya^3 \[Beta]^5 - 32 xa^3 \[Alpha]^3 \[Lambda]^2 - 
        32 xa ya^2 \[Alpha]^3 \[Lambda]^2 + 
        32 xa^2 ya \[Alpha]^2 \[Beta] \[Lambda]^2 + 
        32 ya^3 \[Alpha]^2 \[Beta] \[Lambda]^2 - 
        32 xa^3 \[Alpha] \[Beta]^2 \[Lambda]^2 - 
        32 xa ya^2 \[Alpha] \[Beta]^2 \[Lambda]^2 + 
        32 xa^2 ya \[Beta]^3 \[Lambda]^2 + 
        32 ya^3 \[Beta]^3 \[Lambda]^2 + 48 xa^3 \[Alpha]^3 \[Rho]^2 + 
        48 xa ya^2 \[Alpha]^3 \[Rho]^2 + 
        48 xa^2 ya \[Alpha]^2 \[Beta] \[Rho]^2 + 
        48 ya^3 \[Alpha]^2 \[Beta] \[Rho]^2 + 
        48 xa^3 \[Alpha] \[Beta]^2 \[Rho]^2 + 
        48 xa ya^2 \[Alpha] \[Beta]^2 \[Rho]^2 + 
        48 xa^2 ya \[Beta]^3 \[Rho]^2 + 48 ya^3 \[Beta]^3 \[Rho]^2 + 
        16 xa^3 \[Alpha] \[Lambda]^2 \[Rho]^2 + 
        16 xa ya^2 \[Alpha] \[Lambda]^2 \[Rho]^2 - 
        16 xa^2 ya \[Beta] \[Lambda]^2 \[Rho]^2 - 
        16 ya^3 \[Beta] \[Lambda]^2 \[Rho]^2 - 
        16 xa^3 \[Alpha] \[Rho]^4 - 16 xa ya^2 \[Alpha] \[Rho]^4 - 
        16 xa^2 ya \[Beta] \[Rho]^4 - 
        16 ya^3 \[Beta] \[Rho]^4) #1 + (24 xa^2 \[Alpha]^6 + 
        8 ya^2 \[Alpha]^6 + 32 xa ya \[Alpha]^5 \[Beta] + 
        56 xa^2 \[Alpha]^4 \[Beta]^2 + 40 ya^2 \[Alpha]^4 \[Beta]^2 + 
        64 xa ya \[Alpha]^3 \[Beta]^3 + 
        40 xa^2 \[Alpha]^2 \[Beta]^4 + 56 ya^2 \[Alpha]^2 \[Beta]^4 + 
        32 xa ya \[Alpha] \[Beta]^5 + 8 xa^2 \[Beta]^6 + 
        24 ya^2 \[Beta]^6 + 48 xa^2 \[Alpha]^4 \[Lambda]^2 + 
        16 ya^2 \[Alpha]^4 \[Lambda]^2 + 
        32 xa^2 \[Alpha]^2 \[Beta]^2 \[Lambda]^2 - 
        32 ya^2 \[Alpha]^2 \[Beta]^2 \[Lambda]^2 - 
        16 xa^2 \[Beta]^4 \[Lambda]^2 - 
        48 ya^2 \[Beta]^4 \[Lambda]^2 + 
        24 xa^2 \[Alpha]^2 \[Lambda]^4 + 
        8 ya^2 \[Alpha]^2 \[Lambda]^4 - 
        32 xa ya \[Alpha] \[Beta] \[Lambda]^4 + 
        8 xa^2 \[Beta]^2 \[Lambda]^4 + 
        24 ya^2 \[Beta]^2 \[Lambda]^4 - 52 xa^2 \[Alpha]^4 \[Rho]^2 - 
        20 ya^2 \[Alpha]^4 \[Rho]^2 - 
        64 xa ya \[Alpha]^3 \[Beta] \[Rho]^2 - 
        72 xa^2 \[Alpha]^2 \[Beta]^2 \[Rho]^2 - 
        72 ya^2 \[Alpha]^2 \[Beta]^2 \[Rho]^2 - 
        64 xa ya \[Alpha] \[Beta]^3 \[Rho]^2 - 
        20 xa^2 \[Beta]^4 \[Rho]^2 - 52 ya^2 \[Beta]^4 \[Rho]^2 - 
        40 xa^2 \[Alpha]^2 \[Lambda]^2 \[Rho]^2 - 
        8 ya^2 \[Alpha]^2 \[Lambda]^2 \[Rho]^2 + 
        8 xa^2 \[Beta]^2 \[Lambda]^2 \[Rho]^2 + 
        40 ya^2 \[Beta]^2 \[Lambda]^2 \[Rho]^2 - 
        4 xa^2 \[Lambda]^4 \[Rho]^2 - 4 ya^2 \[Lambda]^4 \[Rho]^2 + 
        32 xa^2 \[Alpha]^2 \[Rho]^4 + 16 ya^2 \[Alpha]^2 \[Rho]^4 + 
        32 xa ya \[Alpha] \[Beta] \[Rho]^4 + 
        16 xa^2 \[Beta]^2 \[Rho]^4 + 32 ya^2 \[Beta]^2 \[Rho]^4 + 
        8 xa^2 \[Lambda]^2 \[Rho]^4 - 8 ya^2 \[Lambda]^2 \[Rho]^4 - 
        4 xa^2 \[Rho]^6 - 4 ya^2 \[Rho]^6) #1^2 + (-8 xa \[Alpha]^7 - 
        8 ya \[Alpha]^6 \[Beta] - 24 xa \[Alpha]^5 \[Beta]^2 - 
        24 ya \[Alpha]^4 \[Beta]^3 - 24 xa \[Alpha]^3 \[Beta]^4 - 
        24 ya \[Alpha]^2 \[Beta]^5 - 8 xa \[Alpha] \[Beta]^6 - 
        8 ya \[Beta]^7 - 24 xa \[Alpha]^5 \[Lambda]^2 - 
        8 ya \[Alpha]^4 \[Beta] \[Lambda]^2 - 
        16 xa \[Alpha]^3 \[Beta]^2 \[Lambda]^2 + 
        16 ya \[Alpha]^2 \[Beta]^3 \[Lambda]^2 + 
        8 xa \[Alpha] \[Beta]^4 \[Lambda]^2 + 
        24 ya \[Beta]^5 \[Lambda]^2 - 24 xa \[Alpha]^3 \[Lambda]^4 + 
        8 ya \[Alpha]^2 \[Beta] \[Lambda]^4 + 
        8 xa \[Alpha] \[Beta]^2 \[Lambda]^4 - 
        24 ya \[Beta]^3 \[Lambda]^4 - 8 xa \[Alpha] \[Lambda]^6 + 
        8 ya \[Beta] \[Lambda]^6 + 24 xa \[Alpha]^5 \[Rho]^2 + 
        24 ya \[Alpha]^4 \[Beta] \[Rho]^2 + 
        48 xa \[Alpha]^3 \[Beta]^2 \[Rho]^2 + 
        48 ya \[Alpha]^2 \[Beta]^3 \[Rho]^2 + 
        24 xa \[Alpha] \[Beta]^4 \[Rho]^2 + 
        24 ya \[Beta]^5 \[Rho]^2 + 
        32 xa \[Alpha]^3 \[Lambda]^2 \[Rho]^2 - 
        32 ya \[Beta]^3 \[Lambda]^2 \[Rho]^2 + 
        8 xa \[Alpha] \[Lambda]^4 \[Rho]^2 + 
        8 ya \[Beta] \[Lambda]^4 \[Rho]^2 - 
        24 xa \[Alpha]^3 \[Rho]^4 - 
        24 ya \[Alpha]^2 \[Beta] \[Rho]^4 - 
        24 xa \[Alpha] \[Beta]^2 \[Rho]^4 - 
        24 ya \[Beta]^3 \[Rho]^4 - 
        8 xa \[Alpha] \[Lambda]^2 \[Rho]^4 + 
        8 ya \[Beta] \[Lambda]^2 \[Rho]^4 + 8 xa \[Alpha] \[Rho]^6 + 
        8 ya \[Beta] \[Rho]^6) #1^3 + (\[Alpha]^8 + 
        4 \[Alpha]^6 \[Beta]^2 + 6 \[Alpha]^4 \[Beta]^4 + 
        4 \[Alpha]^2 \[Beta]^6 + \[Beta]^8 + 
        4 \[Alpha]^6 \[Lambda]^2 + 
        4 \[Alpha]^4 \[Beta]^2 \[Lambda]^2 - 
        4 \[Alpha]^2 \[Beta]^4 \[Lambda]^2 - 
        4 \[Beta]^6 \[Lambda]^2 + 6 \[Alpha]^4 \[Lambda]^4 - 
        4 \[Alpha]^2 \[Beta]^2 \[Lambda]^4 + 
        6 \[Beta]^4 \[Lambda]^4 + 4 \[Alpha]^2 \[Lambda]^6 - 
        4 \[Beta]^2 \[Lambda]^6 + \[Lambda]^8 - 
        4 \[Alpha]^6 \[Rho]^2 - 12 \[Alpha]^4 \[Beta]^2 \[Rho]^2 - 
        12 \[Alpha]^2 \[Beta]^4 \[Rho]^2 - 4 \[Beta]^6 \[Rho]^2 - 
        8 \[Alpha]^4 \[Lambda]^2 \[Rho]^2 + 
        8 \[Beta]^4 \[Lambda]^2 \[Rho]^2 - 
        4 \[Alpha]^2 \[Lambda]^4 \[Rho]^2 - 
        4 \[Beta]^2 \[Lambda]^4 \[Rho]^2 + 6 \[Alpha]^4 \[Rho]^4 + 
        12 \[Alpha]^2 \[Beta]^2 \[Rho]^4 + 6 \[Beta]^4 \[Rho]^4 + 
        4 \[Alpha]^2 \[Lambda]^2 \[Rho]^4 - 
        4 \[Beta]^2 \[Lambda]^2 \[Rho]^4 - 2 \[Lambda]^4 \[Rho]^4 - 
        4 \[Alpha]^2 \[Rho]^6 - 
        4 \[Beta]^2 \[Rho]^6 + \[Rho]^8) #1^4 &, 1]} *)
POSTED BY: Daniel Lichtblau

I think it would be much easier to keep the map w=f[z] in the complex plane. If you want to invert the map you need to solve for z=f^-1[z] . Mathematica usually can handle it, for example:

In[1]:= Solve[a z + b/z == w, z]

In[2]:= Solve[a (z - z0) + b/(z - z0) == w, z]

Out[2]= {{z -> (w - Sqrt[-4 a b + w^2] + 2 a z0)/(2 a)}, {z -> (
   w + Sqrt[-4 a b + w^2] + 2 a z0)/(2 a)}}
POSTED BY: Kay Herbert
SALIOU TELLY
SALIOU TELLY
Posted 9 years ago

Thanks Kay!

I will give it a try in the complex domain where it was first derived. However, the map in the complex form (w = f(z)) involved magnitude of z ( |z| ), which you can see in the algebraic form as sqrt (xd^2 + yd^2)... I was not sure would be easily inverted by Mathematica or any other tool.

But it is worth a try and thanks for the suggestion....

Regards,

Saliou
POSTED BY: SALIOU TELLY

All depends, but usually you get an answer if it exists. Example:

In[9]:= Solve[w == (z - z0)/Abs[z] + 1/(z Abs[z]), z]

Out[9]= {{z -> (z0 - Sqrt[-4 - 4 w + z0^2])/(2 (1 + w))}, {z -> (
   z0 + Sqrt[-4 - 4 w + z0^2])/(
   2 (1 + w))}, {z -> (-z0 - Sqrt[-4 + 4 w + z0^2])/(
   2 (-1 + w))}, {z -> (-z0 + Sqrt[-4 + 4 w + z0^2])/(2 (-1 + w))}}

You can also try Reduce
POSTED BY: Kay Herbert
SALIOU TELLY
SALIOU TELLY
Posted 9 years ago

Thanks Kay!

This seems promising as it does appear to be able to solve in the complex form. I will look into the solution in more detail for correctness and also see if I can re-express it in Cartesian form, which is really the ideal form that I would need to work with.

I am more of a Matlab person but I am amazed by the power of Mathematica when it comes to symbolic calculations.....

Thanks again for your time,

Saliou

POSTED BY: SALIOU TELLY
SALIOU TELLY
SALIOU TELLY
Posted 9 years ago

Good Day Kay,

I explore more into the solutions that Solve provide in my case and quickly realized that it is assuming w and z to be real instead of complex.

By that I mean that Abs[z] in the example you provided is simply treated as the absolute value of the real variable z as opposed to magnitude of the complex variable z. The solution is actually the same if you were to get rid of Abs function.

I have been playing around with Solve and Reduce to figure if one can specify a domain for some of the variables in the equation, but have had some challenges with it.

Below is the complex form of the map that I am actually trying solve:

$$w = \frac{z \left (\left(\frac{\rho z}{\left|z\right|} + s\right)^2+\lambda ^2\right)}{2 \left(\frac{\rho z}{\left|z\right|}+s\right)}$$

Here $\rho$ and $\lambda$ are real but $w$, $z$, and $s$ are all complex with $s$ being just a complex constant parameter (although that should not be relevant). So my interest is in solving for $z$ as function of $w$ and the other constant parameters.

I thought reduce was going to work but it has not yield a solution ... I am checking into its scope and that of Solve to better understand them and would appreciate any suggestion....

Thanks,

Saliou
POSTED BY: SALIOU TELLY

It would be more easy to test this if Mathematica code were provided.
POSTED BY: Daniel Lichtblau
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract