Good day all!
I am somewhat new to mathematica and has been working on trying to find the inverse map to a mapping that I have analytically formulated (Note that the formulation was first done in the complex domain before being expressed in the cartesian form). The formulated cartesian equations below map a 2-D annulus to an annular airfoil as shown in the figures.
$$\text{xa} = \frac{1}{2} \left(\frac{\lambda ^2 \left(\text{xd}^2+\text{yd}^2\right) \left(\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)}{\left(\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)^2+\left(\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)^2}+\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)$$
$$\text{ya} = \frac{1}{2} \left(-\frac{\lambda ^2 \left(\text{xd}^2+\text{yd}^2\right) \left(\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)}{\left(\alpha \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{xd}\right)^2+\left(\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)^2}+\beta \sqrt{\text{xd}^2+\text{yd}^2}+\rho \text{yd}\right)$$
Here ( $\text{xa}$,$\text{ya} $) are coordinates of points on the airfoil annulus, which are mapped points from ($\text{xd} $,$\text{yd} $) on the circular annulus. Everything else are just constant parameters; in the figures shown $\rho = 2$; $\alpha = -.25$; $\beta = 0$; $\lambda = 1.75$; and the circular annulus has outer diameter of 2 units and inner diameter of 1 unit.
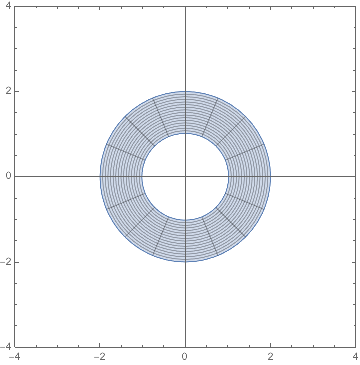
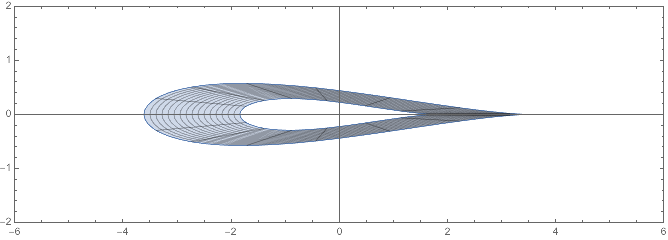
Now, I am interested in finding the inverse map. In other words, I would like to express ( $\text{xd}$,$\text{yd} $) as function of ($\text{xa} $,$\text{ya}$), if possible.
I have not been successful in doing so analytically, and I was hoping that with mathematica I would be able to symbolically solve for the inverse map with "Solve". However, "Solve" has not provided any output (may be because of computational limitation).
Is there any reason why this inverse map will not exist?
I am fairly familiar with the inverse function theorem and thought the inverse would exist at most points despite the cusp at the trailing edge.
If the inverse map exists, am I limited by the computational power of my machine or is there any other approach that can help?
Any assistance in the right direction will be greatly appreciated...
Saliou Telly