Dear All,
Just an hour ago I saw this post at Gizmodo:
Can You Solve the UK Intelligence Agency's Christmas Puzzle?
I was intrigued! The puzzle was given as an image: 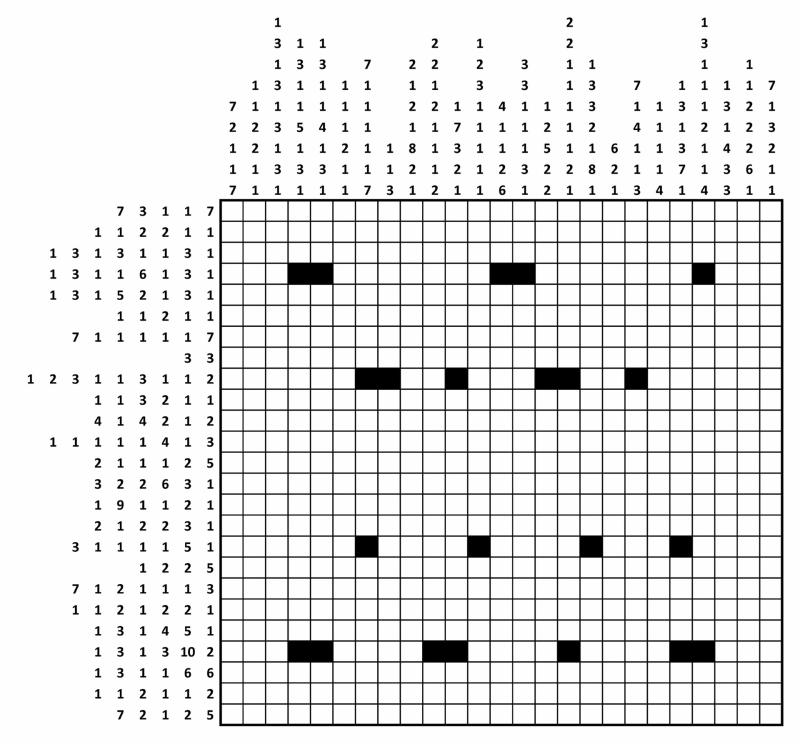
Where the numbers before each row/column denotes that there should be n consecutive blocks in that row. Between each block there must be at least one delimiter (a white cell). So I quickly made a solver, to solve this puzzle:
ClearAll[SpacesDistributeOverN, Possibilities, CheckCommons, FilterPossibilities, GetRow, GetColumn, SetRow, SetColumn, TryRow, TryColumn, ShowAdvancedGrid]
SpacesDistributeOverN[s_, p_] := Flatten[Permutations /@ (Join[#, ConstantArray[0, p - Length[#]]] & /@ IntegerPartitions[s, p]), 1]
Possibilities[hint_, len_] := Module[{p = hint, l = len, b = Length[hint]},
Spaces = # + (Prepend[Append[ConstantArray[1, b - 1], 0], 0]) & /@ (SpacesDistributeOverN[l - Total@p - (b - 1), b + 1]);
Flatten /@ (Riffle[#, Map[Table[1, {#}] &, p, {1}]] & /@ Map[Table[0, {#}] &, Spaces, {2}])
]
CheckCommons[possibilities_] := Module[{poss = possibilities, tmp = possibilities[[1]], len = (possibilities[[1]]) // Length, rowequals = Equal @@@ ( possibilities\[Transpose])},
Table[If[rowequals[[i]], tmp[[i]], Null], {i, 1, len}]
]
FilterPossibilities[possibilities_, knowns_] := Cases[possibilities, knowns /. Null -> _]
GetRow[grid_, row_] := grid[[row]]
GetColumn[grid_, column_] := (grid\[Transpose])[[column]]
SetRow[grid_, row_, newrow_] := Module[{tmp = grid}, tmp[[row]] = newrow; tmp]
SetColumn[grid_, column_, newcol_] := Module[{tmp = grid\[Transpose]},
tmp[[column]] = newcol;
tmp\[Transpose]
]
TryRow[grid_, row_, clues_] := Module[{},
tmprow = GetRow[grid, row];
newclues = clues[[row]];
tmppos = Possibilities[newclues, tmprow // Length];
tmpfilpos = FilterPossibilities[tmppos, tmprow];
newrow = CheckCommons[tmpfilpos];
SetRow[grid, row, newrow]
]
TryColumn[grid_, column_, clues_] := Module[{},
tmpcol = GetColumn[grid, column];
newclues = clues[[column]];
tmppos = Possibilities[newclues, tmpcol // Length];
tmpfilpos = FilterPossibilities[tmppos, tmpcol];
newcol = CheckCommons[tmpfilpos];
SetColumn[grid, column, newcol]
]
ShowAdvancedGrid[grid_, hc_, vc_] := Module[{},
tmpgrid = grid /. {1 -> Graphics[{Black, Rectangle[]}, ImageSize -> 16],
Null -> Graphics[{Gray, Rectangle[]}, ImageSize -> 16],
0 -> Graphics[{White, Rectangle[]}, ImageSize -> 16]};
{dimy, dimx} = grid // Dimensions;
maxhlen = Max[Length /@ hc];
newhclues = Join[Table[Null, {maxhlen - Length[#]}], #] & /@ hc;
maxvlen = Max[Length /@ vc];
newvclues = Join[Table[{Null}, {maxhlen}], vc];
newvclues = Join[Table[Null, {maxvlen - Length[#]}], #] & /@ newvclues;
tmpgrid = Table[Join[newhclues[[i]], tmpgrid[[i]]], {i, 1, dimy}];
tmpgrid = tmpgrid\[Transpose];
tmpgrid = Table[Join[newvclues[[i]], tmpgrid[[i]]], {i, 1, dimx + maxhlen}];
tmpgrid = tmpgrid\[Transpose];
Grid[tmpgrid, Frame -> None, Alignment -> Center, ItemSize -> {1, 1}, Spacings -> {0, 0}]
]
Those are the helper and visualisation functions, now we need the clues and the simple algorithm to solve it:
hclues = {
{7, 3, 1, 1, 7},
{1, 1, 2, 2, 1, 1},
{1, 3, 1, 3, 1, 1, 3, 1},
{1, 3, 1, 1, 6, 1, 3, 1},
{1, 3, 1, 5, 2, 1, 3, 1},
{1, 1, 2, 1, 1},
{7, 1, 1, 1, 1, 1, 7},
{3, 3},
{1, 2, 3, 1, 1, 3, 1, 1, 2},
{1, 1, 3, 2, 1, 1},
{4, 1, 4, 2, 1, 2},
{1, 1, 1, 1, 1, 4, 1, 3},
{2, 1, 1, 1, 2, 5},
{3, 2, 2, 6, 3, 1},
{1, 9, 1, 1, 2, 1},
{2, 1, 2, 2, 3, 1},
{3, 1, 1, 1, 1, 5, 1},
{1, 2, 2, 5},
{7, 1, 2, 1, 1, 1, 3},
{1, 1, 2, 1, 2, 2, 1},
{1, 3, 1, 4, 5, 1},
{1, 3, 1, 3, 10, 2},
{1, 3, 1, 1, 6, 6},
{1, 1, 2, 1, 1, 2},
{7, 2, 1, 2, 5}
};
vclues = {{7, 2, 1, 1, 7},
{1, 1, 2, 2, 1, 1},
{1, 3, 1, 3, 1, 3, 1, 3, 1},
{1, 3, 1, 1, 5, 1, 3, 1},
{1, 3, 1, 1, 4, 1, 3, 1},
{1, 1, 1, 2, 1, 1},
{7, 1, 1, 1, 1, 1, 7},
{1, 1, 3},
{2, 1, 2, 1, 8, 2, 1},
{2, 2, 1, 2, 1, 1, 1, 2},
{1, 7, 3, 2, 1},
{1, 2, 3, 1, 1, 1, 1, 1},
{4, 1, 1, 2, 6},
{3, 3, 1, 1, 1, 3, 1},
{1, 2, 5, 2, 2},
{2, 2, 1, 1, 1, 1, 1, 2, 1},
{1, 3, 3, 2, 1, 8, 1},
{6, 2, 1},
{7, 1, 4, 1, 1, 3},
{1, 1, 1, 1, 4},
{1, 3, 1, 3, 7, 1},
{1, 3, 1, 1, 1, 2, 1, 1, 4},
{1, 3, 1, 4, 3, 3},
{1, 1, 2, 2, 2, 6, 1},
{7, 1, 3, 2, 1, 1}};
{hsize, vsize} = {vclues // Length, hclues // Length};
Total[Flatten[vclues]]
Total[Flatten[hclues]] (* should be equal! *)
(*initialize grid*)
grid = Table[Null, {vsize}, {hsize}] ;
(* these two hints are necessary not more... *)
grid[[9, -7]] = 1;
grid[[-9, 12]] = 1;
oldgrid =.;
RowColumn = 1;
first = 0;
While[! (grid === oldgrid),
If[first == 0,
Do[grid = TryRow[grid, i, hclues], {i, vsize}];
Do[grid = TryColumn[grid, i, vclues], {i, hsize}];
first = 1
];
oldgrid = grid;
RowColumn *= -1;
If[RowColumn == 1,
Do[grid = TryColumn[grid, i, vclues], {i, hsize}];,
Do[grid = TryRow[grid, i, hclues], {i, vsize}];
];
]
ShowAdvancedGrid[grid, hclues, vclues]
Giving:

So we solved it! Now let's see where this hint leads us:
BarcodeRecognize[(1 - grid) // Image]
www.gchq.gov.uk/puzz
At this moment the entire website is down, but as soon as it is up, the next puzzle should be there! Happy Puzzling!