Hi,
I made a mess-up there. The data file I posted was not the raw data, but had been smoothed already. I attach the correct file, which I call "derrived-capacitance-data-in-Hz-and-Farads.txt"
I can be more specific about what I want to do, but it might make it more tricky to understand. I was a bit reluctant to describe it in too much detail, as I thought I'd just make the issue more confusing. But since Jim asked, this describes what I really want to do.
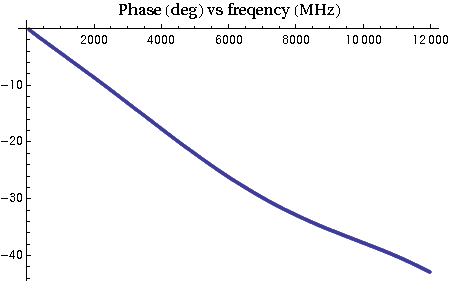
1) Measure a set of phase values, phi up to 12 GHz. These are shown in the file original-phase-data-in-MHz-and-degrees.txt. The first column is frequency in MHz, and the second is the phase in degrees.
This experimentally measured phase values look fairly smooth. Note the phase is almost linear with frequency. Higher frequencies result in larger phase shifts.
2) Compute the capacitance C from that phase data, using the formula. C=-Tan[phase/2]/(100 Pi f) - where phase is in radians and f is in Hz.
That looks rather noisy, and is shown in the file derrived-capacitance-data-in-Hz-and-Farads.txt
It is somewhat puzzling that a fairly clean looking set of phase data results in a rather noisy set of capacitance data.
3) Model the capacitor as a third order polynomial.
4) Varying the frequency from DC to 12 GHz, I want to compute a second set of phase values based on the model of the capacitor. That will be by just re-arranging the above equation. This set of phase data should be quite smooth, as it will be based on a smooth curve for the capacitor.
5) Reduce the RMS error between the original measured phases and the new set based on a third order fit of capacitance.
Fitting over two ranges may be an option, but I'd really like to get one set of data that does a reasonable job over the whole range. Having improved, but separate sets of coefficients for a more restricted frequency range is certainly something I will consider. But the coefficients for the fit must be entered into an instrument which only accepts a 3rd order polynomial fit.
 Attachments:
Attachments: