Message Boards Message Boards

Chaos - Stochastics - Cellular Automata

Since very early on Stephen Wolfram was interested in how simple rules can lead to very complex behaviour and that interest has obviously not ceased until today. I will look into a couple of very simple examples that would be described as chaotic, stochastic systems and cellular automata and the relationships between them.

I will show how we can use stochastic processes that are related to chaotic systems to generate images just like this:

enter image description here

which I think could easily go on one of Sheldon's T-shirt on the @bigbangtheory.

Chaotic Systems

Let's start with a simple chaotic system. It is probably one of the simplest of all chaotic systems: the Bernoulli shift map. 

HoldForm[Subscript[x, n + 1] = Mod[2 Subscript[x, n], 1]] // TraditionalForm

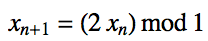
enter image description here

It is a really simple rule. Start with a real (normal) number between 0 and 1, multiply the last value by 2 and make sure that the digit on the left of the point is zero. We can easily plot this in Mathematica. 

NestList[Mod[2 #, 1] &, 1/Sqrt[2], 100] // ListLinePlot

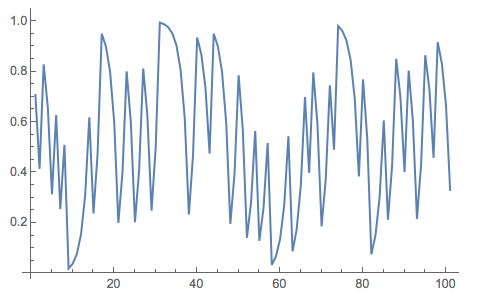
enter image description here

It looks quite erratic, but it is actually deterministic. Given the initial value and iterating a deterministic rule you can compute all the future of the system. The structure behind this simple process can be visualised using a scatterplot:

ListPlot[Partition[NestList[Mod[2 #, 1] &, 1/Sqrt[2], 300], 2, 1]]

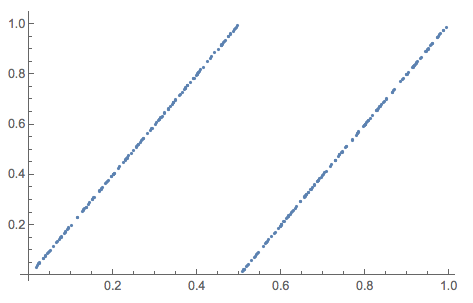
enter image description here

This is actually the function on the right hand side of our recurrence relation:

Plot[Mod[2 x, 1], {x, 0, 1}]

enter image description here

The scatterplot illustrates the simple rule behind this iteration. Which is deterministic. We can also observe that this map is very sensitive to its initial conditions. 

\[Delta] = 10^-10; 
{NestList[Mod[2 #, 1] &, 1/Sqrt[2], 60], NestList[Mod[2 #, 1] &, 1/Sqrt[2] + \[Delta], 60]} // ListLinePlot

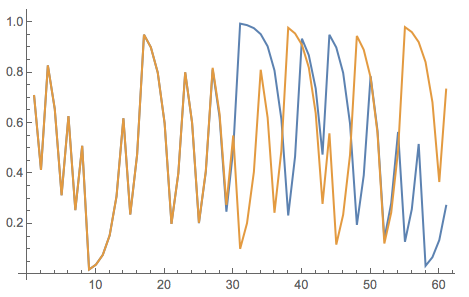
enter image description here

This shows that even if the initial conditions are only off by $10^{-10}$ after about 20 steps the paths diverge and behave very differently. This is of course all known; Ed Lorenz used the term "butterfly effect" for this kind of thing. You will have noticed that I used a very strange unusual intitial condition $1/\sqrt{2}$. This has a reason. It turns out that you need to start at what is called a "normal number".

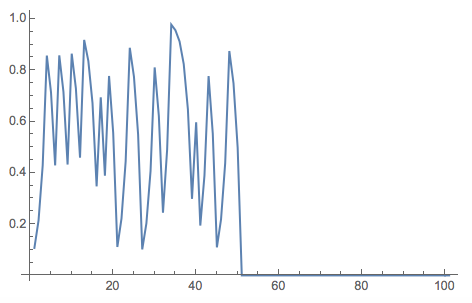
enter image description here

enter image description here

This basically means that you have to start at a number, the digits of which are generated randomly - a random initial condition. If you started at a finite precision number (like machine precision), i.e. a number where after a finite number of digits there are only zeros, then this function would stop behaving erratically but rather go to a constant zero: 

NestList[Mod[2 #, 1] &, RandomReal[], 100] // ListLinePlot

enter image description here

A similar problem happens when you start at numbers with a periodic (binary/decimal) expansion.

NestList[Mod[2 #, 1] &, 1/3, 100] // ListLinePlot

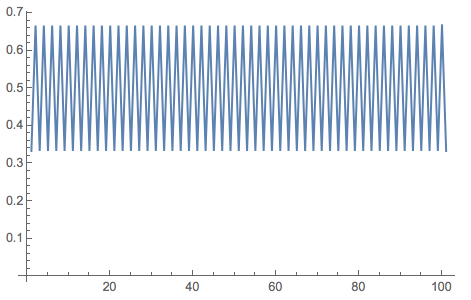
enter image description here

Now the time series is periodic. Neither situation (fixed point or periodic) are typical in the sense that if you randomly pick an initial condition, you obtain a chaotic sequence with probability one. Normal numbers have measure one; typically you would pick a normal number, which is problematic when using many programming languages naivly.

This is a nightmare for simulations of some chaotic systems, as you cannot really generate long time series, because of finite precision. As you see above there is no such problem in Mathemtica when you calculate with infinite precision, i.e. when I use $1/\sqrt{2}$. Of course, I can overcome the problem in the last figure by just increasing the precision:

NestList[Mod[2 #, 1] &, RandomReal[1, WorkingPrecision -> 150], 100] // ListLinePlot

As long as the working precision is a bit larger than the number of iterations the time series will be correct. It is interesting to note that on many machines this problem does not actually present it self (at least not for reasonably long time series). If you program this in C/C++ you can usually do many more iterations then what correponds to the MachinePrecision. This is because the processor " effectively adds" random last digits as you iterate - this is not a very good description, but should suffice for now. In that particular case it actually helps. There is a famous shadowing lemma which allows to conclude that the so generated time series is [Delta] close to a "proper" time series with infinite precision.

One further observation is that the Bernoulli shift map becomes really simple in base 2. This is because in base two multiplication by 2 only shifts all digits one to the left - just like multiplication by 10 in base 10. 

TableForm[BaseForm[#, 2] & /@ NestList[Mod[2 #, 1] &, RandomReal[1, WorkingPrecision -> 10], 40]]

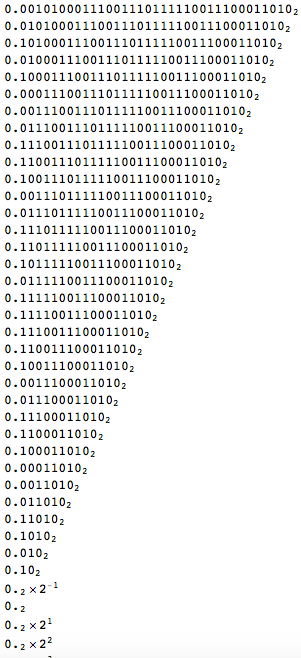
enter image description here

The first line corresponds to our (finite) precision intinial condition. Then we iterate and as you can see the sequence is shifted to the left and any potential nonzero digit on the left of the point is deleted. You also notice that after a certain number of iterations the hole thing goes numerically to zero.

This shifting behaviour in base 2 will become important now.

Stochastic systems with time reversal

Let's give the story a nice twist. The idea is taken from this paper; for a very readable description see here. In the section on chaos we had a deterministic system with random initial conditions. Let's go to a stochastic system like so:

HoldForm[Subscript[x, n + 1] = 1/2 Subscript[x, n] + 1/2 RandomChoice[{1, 2}]] // TraditionalForm

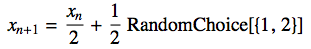
enter image description here

This system would usually be considered to be stochastic. Its dynamics is mainly determined by previous values plus noise similar to ARProcesses. The curious thing is that if I time reverse the resulting time series, the system becomes identical to the chaotic system in part one!

ListLinePlot[Reverse@NestList[1/2 # + 1/2 RandomChoice[{0, 1}] &, RandomReal[], 40]]

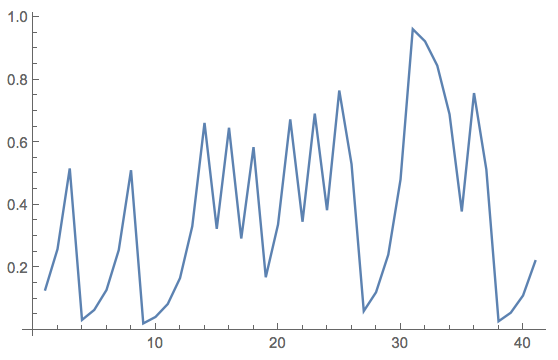
enter image description here

This time series does not fully make my point so let me be a bit clearer. First we choose an initial condition (and try to be a bit generous about the number of digits):

start = RandomReal[1, WorkingPrecision -> 400];

Then we generate our time series and plot:

tsdeterm = NestList[Mod[2 #, 1] &, start, 100];
ListLinePlot[tsdeterm]

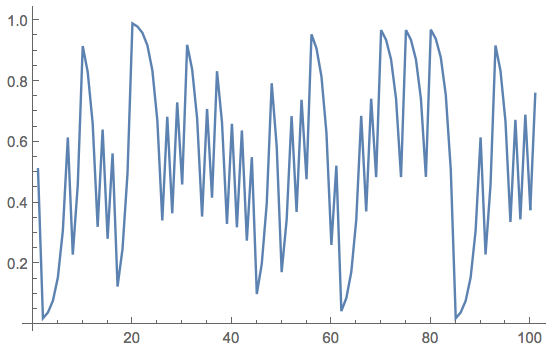
enter image description here

Now comes the trick. I use the 100th value of the time series, and convert it to binary (after padding it on the left with zeros). Then I extract the individual digits:

randomincrements = 
 Join[ConstantArray[0, -RealDigits[tsdeterm[[-100]], 2][[2]]], RealDigits[tsdeterm[[-100]], 2][[1]]];

Finally, I use my stochastic system with these random increments:

results = {tsdeterm[[-1]]}; Do[AppendTo[results, 1/2 results[[-1]] + 1/2 randomincrements[[100 - i]]], {i, 1, 100}]

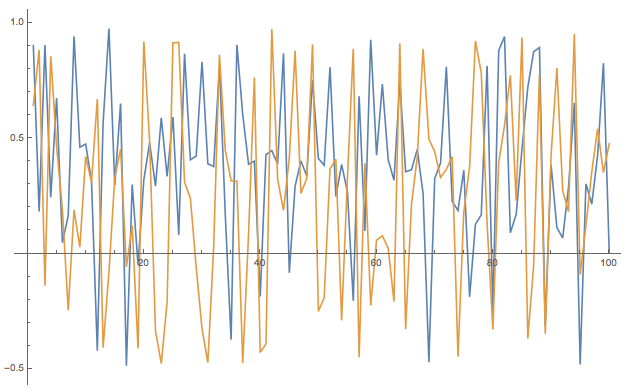
Then I reverse the time series and plot it with the original, deterministic one:

ListLinePlot[{tsdeterm[[1 ;;]], Reverse@results}, PlotStyle -> {{Red, Thick}, {Blue, Dotted}}]

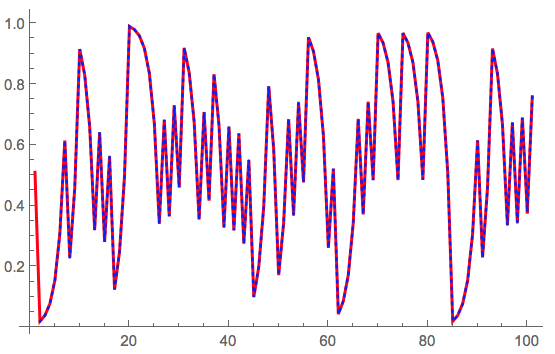
enter image description here

It becomes clear that the two sequences are identical - well at least for long enough random sequences. So basically I used the values of the deterministic sequence (in binary form) as increments of my stochastic time series and get the same result - after time reversal. So my random initial condition acts as "random increments" in my stochastic system and makes them - sort of- equivalent. We can look at the scatter plots of both and they are, of course, identical:

Row[
{ListPlot[Partition[tsdeterm, 2, 1], PlotStyle -> Green, ImageSize -> Medium], 
ListPlot[Partition[Reverse@results, 2, 1], PlotStyle -> Red, ImageSize -> Medium]}]

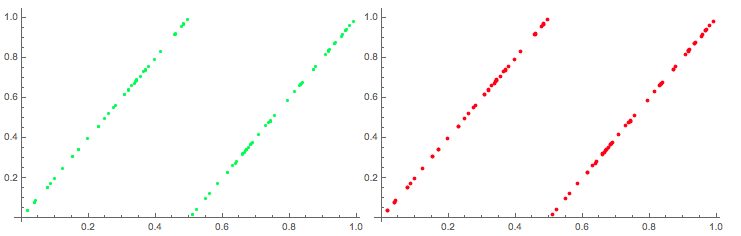
enter image description here

Alternatively and probably easier, I could first generate the random increments and then the corresponding initial condition for the deterministic system. If we generate the (chaotic) time series like this we do not have to care -very much- about the finite precision of the computer arithmetic, which is a huge advantage.

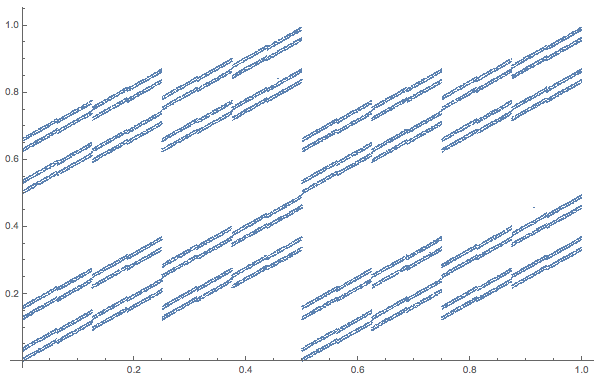
We can now also combine two of these stochastic equations and get some interesting structures - the only really important thing seems to be that the random increments are "very discrete", i.e. that there are only few possible values. 

ListPlot[Reverse@
  NestList[{1/2 #[[1]] + 1/2 RandomChoice[{0, 1}], 1/4 #[[2]] + 1/4 #[[1]] + 1/2 RandomChoice[{0, 1}]} &, RandomReal[1, 2], 45000], PlotMarkers -> {Point, 0.1}]

enter image description here

Or this one:

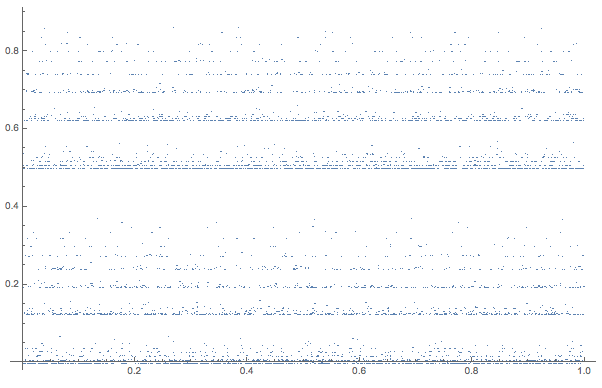
enter image description here

By playing a bit with the functional form of the equations we can achieve some pretty results:

Brushstrokes

databrushstrokes = 
  Reverse@NestList[{1/2 Cos[-0.3 (#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1, 2}] #[[2]], 
      1/2 Sin[#[[1]]]*Cos[#[[2]]] + 1/2 RandomChoice[{0, 1}] #[[1]]} &, RandomReal[1, 2], 1000000];
Graphics[{PointSize[0.0005], Point[databrushstrokes, VertexColors -> (Hue /@ (Norm[#] & /@ brushstrokes))]}, 
 AspectRatio -> 1/GoldenRatio, Axes -> False, Background -> Black, Axes -> False, ImageSize -> Full]

enter image description here

Three ghosts

datathreeghosts = 
  Reverse@NestList[{1/2 Cos[-0.3 (#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1, 2}], 
      1/2 Sin[#[[1]]] + Cos[#[[2]]] + 1/2 RandomChoice[{0, 1, 2}]} &, RandomReal[1, 2], 1000000];
Graphics[{PointSize[0.0005], Point[datathreeghosts, VertexColors -> (Hue /@ (Norm[#] & /@ datathreeghosts))]}, 
 AspectRatio -> 1/GoldenRatio, Axes -> False, Background -> Black, Axes -> False, ImageSize -> Full]

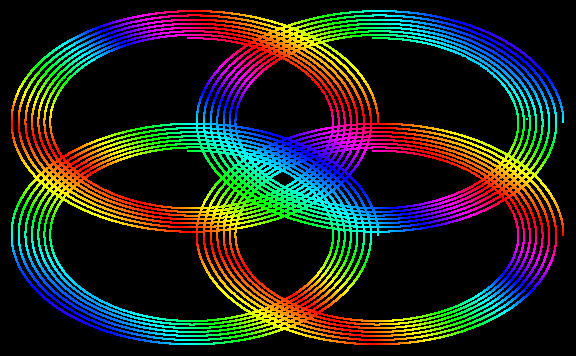
enter image description here

Olympic Rings

dataolympicrings = 
  Reverse@NestList[{1/2 Cos[10 Pi*(#[[1]]^2 + #[[2]]^2)]*Exp[-0.2*(#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1}], 
      1/2 Sin[10 Pi*(#[[1]]^2 + #[[2]]^2)]*Exp[-0.2*(#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1}]} &, RandomReal[1, 2], 600000];
Graphics[{PointSize[0.002], Point[dataolympicrings, VertexColors -> (Hue /@ (Norm[#[[1]] + #[[2]]] & /@ 
 dataolympicrings))]}, AspectRatio -> 1/GoldenRatio, Axes -> False, Background -> Black, Axes -> False, ImageSize -> Large]

enter image description here

Jellyfish

datajellyfish = 
  Reverse@NestList[{1/2 Cos[#[[1]]] + 1/2 Sin[#[[2]]] + 1/2 RandomChoice[{0, 1}] #[[2]], 
      1/2 Cos[#[[2]]] + 1/2 Sin[#[[1]]] + 1/2 RandomChoice[{0, 1}] #[[1]]} &, RandomReal[1, 2], 2000000];
Graphics[{PointSize[0.0002], Point[datajellyfish, VertexColors -> (Hue /@ (Norm[#] & /@ datajellyfish))]}, 
 AspectRatio -> 1, Axes -> False, Background -> Black, Axes -> False, ImageSize -> Full]

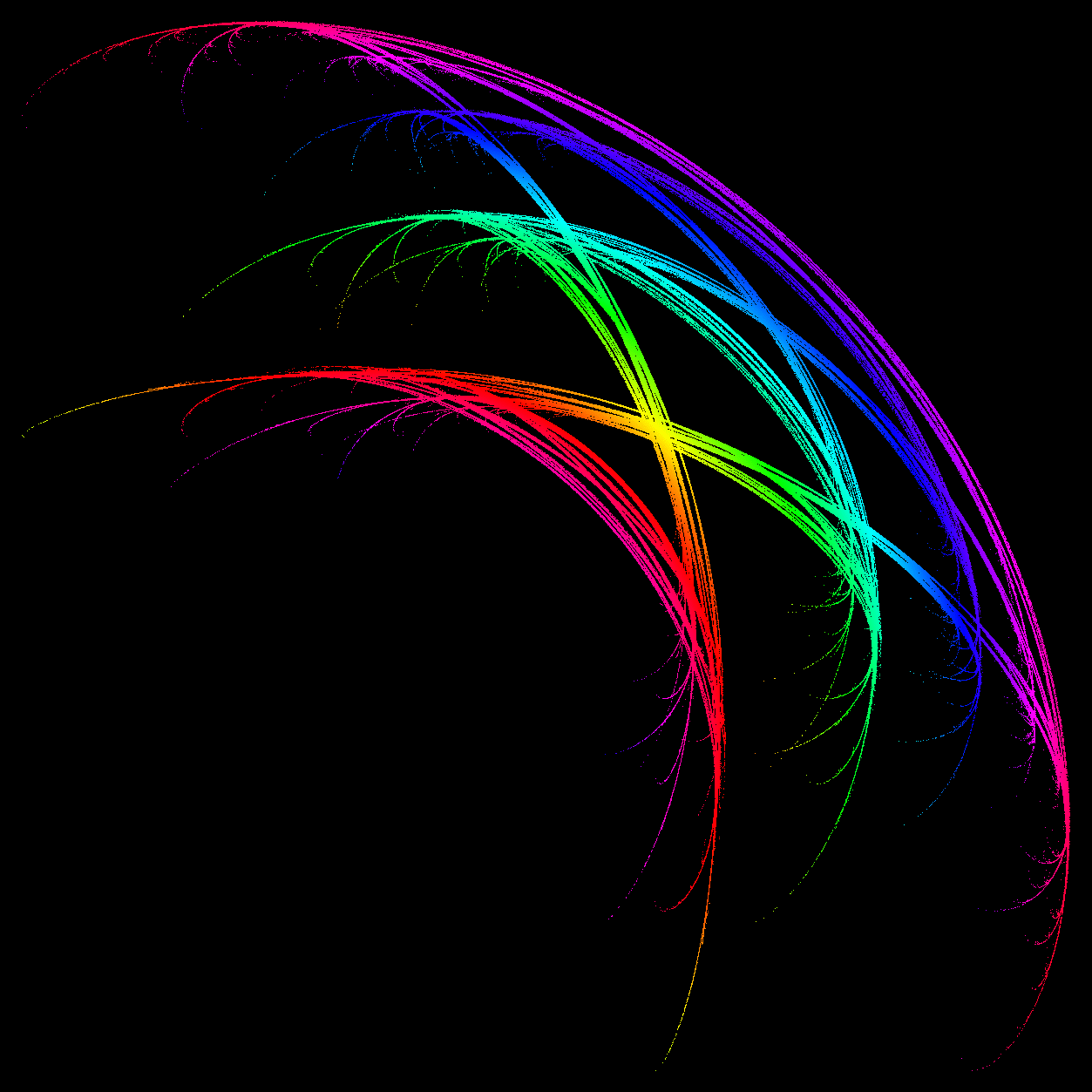
enter image description here

FractalMan with hat

datafractalman = 
  Reverse@NestList[{1/2 Exp[-3 (#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1}], 
  1/2 #[[1]]^#[[2]] + 1/2 RandomChoice[{0, 1}]} &, RandomReal[1, 2], 4000000];
Graphics[{PointSize[0.0004], Point[datafractalman, VertexColors -> (Hue /@ Mean /@ datafractalman)]}, 
 AspectRatio -> 1/GoldenRatio, Axes -> False, Background -> Black, Axes -> False, ImageSize -> Full]

enter image description here

If you just look at the time series everything looks very weird and erratic. Here are the two sequences for the olympic rings:

enter image description here

and here their scatterplot:

ListPlot[Partition[dataolympicrings[[1 ;;, 1]], 2, 1]]

enter image description here

Further examples

Here are some more examples for you to try:

datamesh = 
  Reverse@NestList[{1/2 Cos[10 Pi*(#[[1]]^2 + #[[2]]^2)]*
        Exp[-0.2*(#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1}], 
      1/2 SawtoothWave[10 Pi*(#[[1]]^2 + #[[2]]^2)]*
        Exp[-0.2*(#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1}]} &,
     RandomReal[1, 2], 60000];
Graphics[{PointSize[0.002], 
  Point[datamesh, 
   VertexColors -> (Hue /@ (Norm[#[[1]] + #[[2]]] & /@ datammesh))]}, 
 AspectRatio -> 1/GoldenRatio, Axes -> False, Background -> Black, 
 Axes -> False, ImageSize -> Large]
datasqueezedrings = 
  Reverse@NestList[{1/2 SawtoothWave@Sin[10 Pi*(#[[1]]^2 + #[[2]]^2)]*
        Exp[-0.2*(#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1}], 
      1/2 SawtoothWave@Cos[10 Pi*(#[[1]]^2 + #[[2]]^2)]*
        Exp[-0.2*(#[[1]]^2 + #[[2]]^2)] + 1/2 RandomChoice[{0, 1}]} &,
     RandomReal[1, 2], 100000];
Graphics[{PointSize[0.002], 
  Point[datasqueezedrings, 
   VertexColors -> (Hue /@ (Norm[#[[1]] + #[[2]]] & /@ 
        datasqueezedrings))]}, AspectRatio -> 1/GoldenRatio, 
 Axes -> False, Background -> Black, Axes -> False, ImageSize -> Large]
dataflowers = 
  Reverse@NestList[{1/10 (#[[1]]^2 + #[[2]]^2) + 
       1/2 RandomChoice[{0, 1, 2}], 
      1/3 (Sin[#[[1]]] + Cos[#[[2]]]) + 
       1/2 RandomChoice[{0, 1, 2}]} &, RandomReal[1, 2], 20000];
Graphics[{PointSize[0.002], 
  Point[dataflowers, 
   VertexColors -> (Hue /@ (Norm[#[[1]] + #[[2]]] & /@ 
        dataflowers))]}, AspectRatio -> 1/GoldenRatio, Axes -> False, 
 Background -> Black, Axes -> False, ImageSize -> Large]

These coupled stochastic maps seem to be fractal generators! Ususally fractals are linked to chaotic systems, but there are some exceptions.

Stochastic Sierpinski Triangle

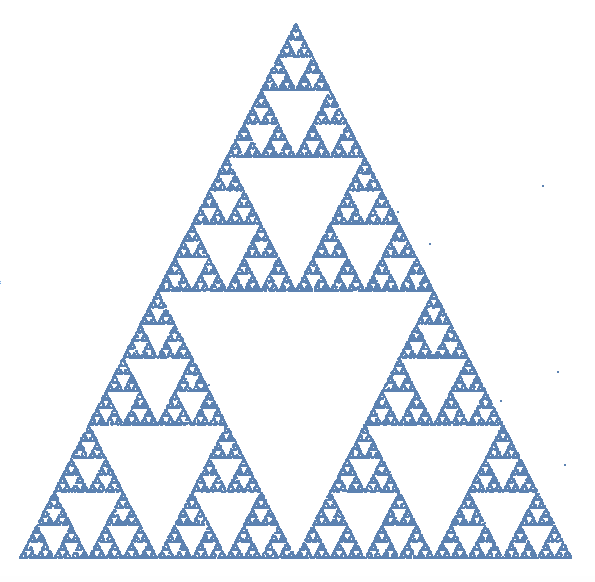
The Sierpinski triangle is a fractal object. You start with a triangle remove a little triangle in the middle and iterate. This is a very deterministic procedure which yields a fractal object. See this demonstration.

It turns out that the same object can be generated by a stochastic procedure: 1. choose a random point in the plane. 2. Construct a triangle; label the three vertices of the first triangle by 1,2,3. 3. Chose a vertex at random and move half way towards it. 4. Iterate step 3.

Here is an implementation of that.

M = 40000; 
randompoints = Table[RandomChoice[{{0., 0.}, {1., 0.}, {0.5, Sqrt[3]/2 // N}}], {i, 1, M}]; results = {RandomReal[1, {2}]}; Table[ 
 AppendTo[results, 0.5*(randompoints[[i]] - results[[-1]]) + results[[-1]]], {i, 1, M}];
ListPlot[results, ImageSize -> Large, AspectRatio -> 1, Axes -> False]

enter image description here

It turns out that this is only one of our stochastic systems with discrete but dependent increments:

data = NestList[
    1/2 ({ 1 #[[1]], #[[2]]} + RandomChoice[{{0., 0.}, {1, 0.}, {0.5, Sqrt[3]/2 // N}}]) &, RandomReal[1, 2], 100000][[5 ;;]];
Graphics[{PointSize[0.0002], Yellow, Point[data(*,VertexColors\[Rule](Hue/@Mean/@data)*)]}, 
 AspectRatio -> 1/GoldenRatio, Axes -> False, Background -> Black, Axes -> False, ImageSize -> Full]

enter image description here

You can now deform this a bit and try things like this:

data = NestList[
    1/2 ({ #[[1]], #[[2]]^1.3} + 
        RandomChoice[{{0., 0.}, {1., 0.}, {0.5, Sqrt[3]/2 // N}}]) &, 
    RandomReal[1, 2], 100000][[5 ;;]];
Graphics[{PointSize[0.0002], Yellow, 
  Point[data(*,VertexColors\[Rule](Hue/@Mean/@data)*)]}, 
 AspectRatio -> 1/GoldenRatio, Axes -> False, Background -> Black, 
 Axes -> False, ImageSize -> Full]

Cellular Automata

Finally, it has repeatedly been observed that cellular automata can also produce chaotic signals. We might therefore want to figure out which cellular automaton corresponds roughly to the Bernoulli Shift Map. We work in binary representation:

CellularAutomaton[170, RandomChoice[{0, 1}, 12], 6] // TableForm

enter image description here

So similar to the Bernoulli Shift Map rule 170 shifts the sequence one step to the left. This means that we can now generate the Bernoulli Shift map with that rule:

N[FromDigits[{#, 0}, 2]] & /@ CellularAutomaton[170, RandomChoice[{0, 1}, 300], 250] // ListLinePlot

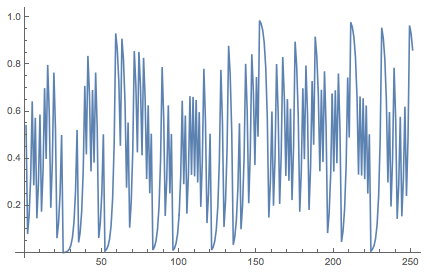
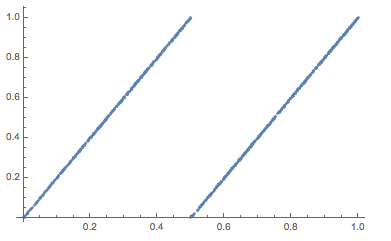
enter image description here

If we look at the scatterplot we can corroborate the typical pattern of the Bernoulli shift map:

ListPlot[Partition[N[FromDigits[{#, 0}, 2]] & /@ CellularAutomaton[170, RandomChoice[{0, 1}, 1000], 950], 2, 1]]

enter image description here

We can now put two of them together to get a two dimensional system. 

ts = {{RandomChoice[{0, 1}, 100], RandomChoice[{0, 1}, 100]}};
Do[AppendTo[ts, {CellularAutomaton[170, ts[[-1, 1]], 1][[2]], CellularAutomaton[170, ts[[-1, 2]], 1][[2]]}], {80}];
ListPlot[{N[FromDigits[{#[[1]], 0}, 2]], N[FromDigits[{#[[2]], 0}, 2]]} & /@ ts]

This is neither fast not elegant but does the job. If we now couple the two equations, but converting to decimal, applying some functions and converting back to binary 

ts = {{RandomChoice[{0, 1}, 40000], RandomChoice[{0, 1}, 40000]}};
Do[AppendTo[ts, {Join[ConstantArray[0, -RealDigits[#, 2][[2]]], 
       RealDigits[#, 2][[1]]] & @(Sin[1.8*N[FromDigits[{CellularAutomaton[170, ts[[-1, 1]], 1][[2]], 0}, 2]] + 
        N[FromDigits[{CellularAutomaton[170, ts[[-1, 2]], 1][[2]], 0},2]]]), Join[ConstantArray[0, -RealDigits[#, 2][[2]]], 
       RealDigits[#, 2][[1]]] & @(1/2 ( N[FromDigits[{CellularAutomaton[170, ts[[-1, 1]], 1][[2]], 0},2]]^3 + 
         N[FromDigits[{CellularAutomaton[170, ts[[-1, 2]], 1][[2]], 0}, 2]]^3.))}], {39900}];
ListPlot[{N[FromDigits[{#[[1]], 0}, 2]], N[FromDigits[{#[[2]], 0}, 2]]} & /@ ts, Axes -> False, 
 Background -> Black, PlotStyle -> Yellow, PlotMarkers -> {Point, 0.1}]

enter image description here

There is nothing really new here, but we do generate some nice images. Many other ideas come to mind, but this post is already much too long, so I will call it a day.

Cheers,

Marco
POSTED BY: Marco Thiel
4 Replies
Sort By:

Dear Marco,

thank you for sharing these very interesting facts on chaotic systems! I have to find time to study this in detail! In particular I find the "reversibility" - your first two models - remarkable. I think one can get at least a feeling on how that surprising feature works: If the dynamics of these models is plotted in the "standard way", then one might well believe that one is the inverse of the other - if instead of RandomChoice binary digits of a trajectory value are used. Here a sketch on what I mean (code attached):

enter image description here

Best regards and again thank you for this nice motivation!

Henrik

Attachments:
POSTED BY: Henrik Schachner

Dear Henrik,

thank you very much for your kind words. You are quite right: your images do indeed visualise the idea very nicely. Very often one illustrates chaotic systems with a metaphor of stretching and folding. In the map $$x_{n+1}=2 x_n \mod 1$$

the $2 x_n$ is a sort of stretching. Points that have a certain distance will basically double that distance after the iteration. This exponentially increases the distance between neighbouring points and thereby "magnifies" the initial conditions, which are random. One can understand that the randomness of the initial conditions becomes a dominating factor for the evolution of the system.

The $\mod 1$ is a kind of folding the it cuts the line in half and merges the two like so:

Export["~/Desktop/strechingfolding.gif", 
 Join[Table[
   Graphics[{Line[{{0, 0}, {t, 0}}]}, 
    PlotRange -> {{-0.5, 2.5}, {-1, 1}}], {t, 1, 2, 0.1}],
  Table[Graphics[{Line[{{0, 0}, {1, 0}}], Red , 
     Line[{{1, t}, {2, t}}]}, 
    PlotRange -> {{-0.5, 2.5}, {-1, 1}}], {t, 0, 0.2, 0.05}],
  Table[Graphics[{Line[{{0, 0}, {1, 0}}], Red, 
     Line[{{1 - t, 0.2}, {2 - t, 0.2}}]}, 
    PlotRange -> {{-0.5, 2.5}, {-1, 1}}], {t, 0, 1, 0.1}],
  Table[Graphics[{Line[{{0, 0}, {1, 0}}], Red, 
     Line[{{0, t}, {1, t}}]}, 
    PlotRange -> {{-0.5, 2.5}, {-1, 1}}], {t, 0.2, 0, -0.05}]]]

enter image description here

So I stretch and fold intervals of points here. The whole thing is not invertable, because when I fold different points are identified. I can imagine the random ones and zeros to "choose" the branch they came from. I can also interpret this as learning more about the initial conditions (that I cannot observe with infinite precision) from the trajectory. Small changes in the initial conditions lead to large (observable) differences in the trajectories, which allow me to infer with higher and higher precision what the initial conditions must have been.

Some time ago I attended a talk by Jim Yorke who highlighted the problem of, for example, predicting the weather due to the problem of the sensitive dependence on initial conditions. He suggested that it might be more valuable to calculate backwards and try to "post-dict" the initial conditions that must have led to this situation.

It is quite fascinating that the "infinite precision" calculations that the Wolfram language can do are particularly useful here. A scientifically very senior colleague of mine here at Aberdeen studied finite precision issue in chaotic systems in the 80's. The Wolfram Language is quite convenient to study these issues.

Thank you very much again for your encouragement.

Cheers,

Marco
POSTED BY: Marco Thiel

enter image description here - another post of yours has been selected for the Staff Picks group, congratulations !

We are happy to see you at the tops of the "Featured Contributor" board. Thank you for your wonderful contributions, and please keep them coming!
POSTED BY: EDITORIAL BOARD

Thanks a lot!!!

imgmatrix = Join[ImageData[img], ImageData[img]];
Manipulate[Image[imgmatrix[[g ;; g + 774, All, All]]], {g, 1, 775, 1}]

enter image description here

frames = Table[
   ParametricPlot3D[{Cos[u] (3 + Cos[v]), Sin[u] (3 + Cos[v]), Sin[v]}, {u, 0, 2 \[Pi]}, {v, 0, 2 \[Pi]}, 
  TextureCoordinateFunction -> ({2 #4, 2 #5} &), PlotStyle -> Directive[Specularity[White, 50], Texture[Image[imgmatrix[[g ;; g + 774, All, All]]]]], Axes -> False, Lighting -> "Neutral", Mesh -> None, Boxed -> False, ImageSize -> 900], {g, 1, 775, 25}];

enter image description here

Marco
POSTED BY: Marco Thiel
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract