At squaring.net, I learned of a triangle with sides based on powers of the real positive root of $d^6-d^2-1=0$.
$$ d = \sqrt{\frac{1}{3} \sqrt[3]{\frac{27}{2}-\frac{3 \sqrt{69}}{2}}+\frac{\sqrt[3]{\frac{1}{2} \left(9+\sqrt{69}\right)}}{3^{2/3}}} = 1.150963925257758035680601218461375863666...$$
d = Root[-1 - #1^2 + #1^6 &, 2];
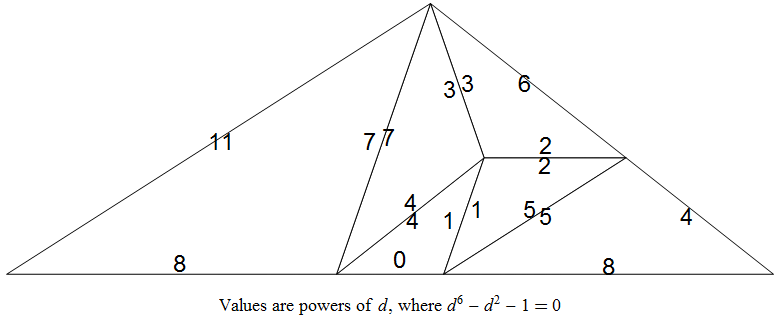
Here's a picture I assembled. The numbers on the sides of the triangle are powers of $d$. The smallest triangle has sides $d^0, d^1, d^4$. The outside triangle has sides $d^{10}, d^{11}, d^{14}$.
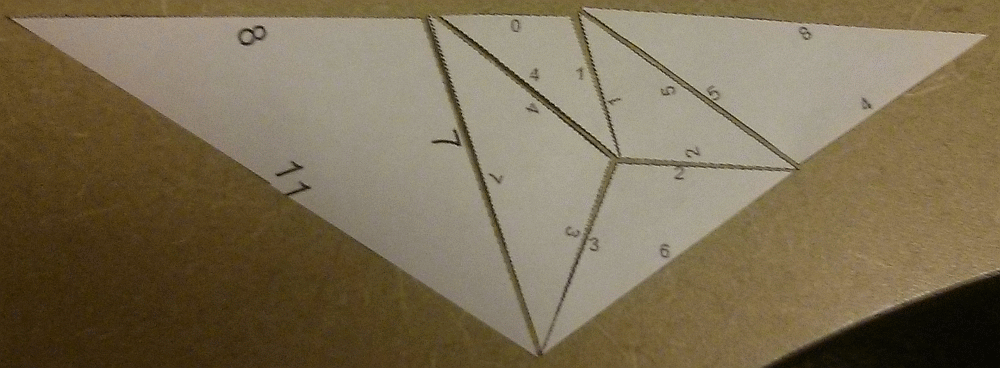
We can get point positions for the triangle vertices with uses of Solve and EuclideanDistance.
zakpts = FullSimplify[{{-d^8, 0}, {0, 0}, {1, 0}, {1 + d^8, 0},
{Root[-5 + 16 #1 - 20 #1^2 + 8 #1^3 &, 1], 1/2 Root[-43 - 18 #1^2 + #1^4 + #1^6 &, 2]},
{Root[-5 + 16 #1 - 20 #1^2 + 8 #1^3 &, 1] + d^2, 1/2 Root[-43 - 18 #1^2 + #1^4 + #1^6 &, 2]},
{Root[-1 + 2 #1 - 8 #1^2 + 8 #1^3 &, 1], Root[-43 + 52 #1^2 - 416 #1^4 + 64 #1^6 &, 2]}}];
From there, it's useful to convert to barycentric coordinates, which give the coordinates of a point in relation to a triangle.
ToBarycentrics[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}}, {p_, q_}] :=
Solve[{m*x1 + n*x2 + (1 - m - n)*x3, m*y1 + n*y2 + (1 - m - n)*y3} == {p, q}];
FromBarycentrics[{m_, n_}, {{x1_, y1_}, {x2_, y2_}, {x3_, y3_}}] :=
{m*x1 + n*x2 + (1 - m - n)*x3, m*y1 + n*y2 + (1 - m - n)*y3};
outsidezak = {{-d^8, 0}, {1 + d^8, 0}, {Root[-1 + 2 #1 - 8 #1^2 + 8 #1^3 &, 1], Root[-43 + 52 #1^2 - 416 #1^4 + 64 #1^6 &, 2]}};
FullSimplify[({m, n} /. ToBarycentrics[outsidezak, #])[[1]] & /@ zakpts]
Cleaning that up, we can get the barycentric version of each triangle.
zakbary = With[{
r1 = Root[-1 + 2 #1 - #1^2 + #1^3 &, 1], r2 = Root[-1 + 3 #1 - 2 #1^2 + #1^3 &, 1],
r3 = Root[-1 + 5 #1 + 2 #1^2 + #1^3 &, 1], r4 = Root[-5 + 14 #1 - 3 #1^2 + #1^3 &, 1]},
{{0, 0}, {0, 1}, {1, 0}, {0, r1}, {r1, r2}, {r2, r1}, {r3, r4}}];
zaktriangles = zakbary[[#]] & /@ {{7, 5, 6}, {4, 6, 7}, {1, 4, 7}, {5, 1, 7}, {6, 2, 4}, {3, 1, 5}};
And from that, we can make a triangle with the edges labeled by their powers.
d = Root[-1 - #1^2 + #1^6 &, 2];
triangles = Map[FromBarycentrics[#, outsidezak] &, zactriangles, {2}];
edges = Partition[N[#], 2, 1, 1] & /@ triangles;
powers = Map[Round[Log[d, EuclideanDistance[#[[1]], #[[2]]]]] &, edges, {2}];
edgetext = Table[{ToString[powers[[a, b]]], N[ ((powers[[a, 1]] - 2) Mean[edges[[a, b]]] +
Mean[triangles[[a]]])/(powers[[a, 1]] - 1)]}, {a, 1, 6}, {b, 1, 3}];
Clear[d];
Column[{Graphics[{FaceForm[White], EdgeForm[Black], Polygon /@ triangles,
Style[Map[Text[#[[1]], #[[2]]] &, edgetext, {2}], 24]}, ImageSize -> {800, Automatic}],
Text@Style[Row[{"Values are powers of ", Style["d", Italic], ", where ",
TraditionalForm[d^6 - d^2 - 1 == 0]}], 18]},
Alignment -> Center]
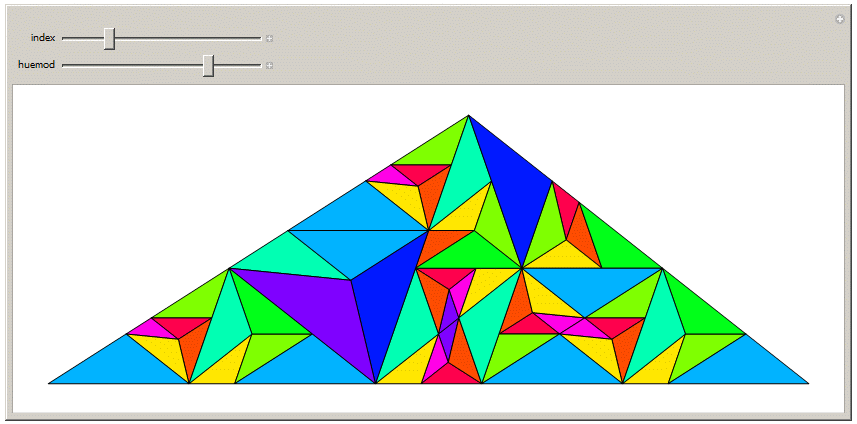
We can also make a fractal out of it, by subdividing the largest triangles.This is where the barycentric coordinates really become useful. The previous figure could have been made from the originally calculated points.
seqoftri = NestList[With[{list = #}, Sort[Flatten[{Drop[list, -1],Transpose[{First[Last[list]] - {10, 9, 8, 7, 6, 3},
Chop[Map[N[FromBarycentrics[#, Last[Last[list]]]] &, zactriangles, {2}]]}]}, 1]]] &,
Transpose[{Min /@ powers, Chop[N[triangles]]}], 50];
Manipulate[Graphics[{FaceForm[White],EdgeForm[Black], {Hue[Mod[First[#] + huemod, 10]/10], Polygon[Last[#]]} & /@
seqoftri[[index]]}, ImageSize -> {800, 300}], {index, 1, 50, 1}, {huemod, 0, 10}, SaveDefinitions -> True]
Do other simple polynomials lend themselves to weird similar triangle dissections?
 Attachments:
Attachments: