Rational Distance Problem is a new Demonstration. I'll start with the discussion there.

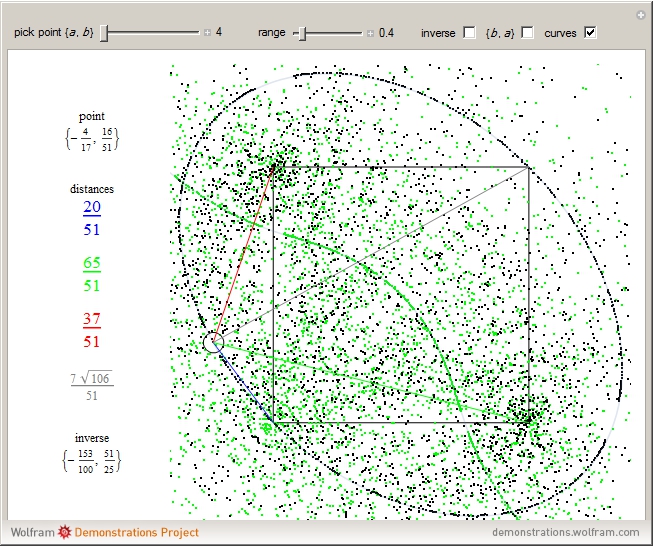
Is there a point at rational distances from the vertices of a unit square? This unsolved question is known as the rational distance problem.

This Demonstration gives 2877 canonical triples, which are points at rational distances from the vertices (0,0), (1,0), and (0,1). These triples were collected by analyzing primitive Heronian triangles (triangles with rational sides and areas). If $(a,b)$ is a triple, so are $(b,a)$ and the inverse $(a,b)/(a^2+b^2)$, so each triple gives three others.

A triple has rational coordinates. Consider the squares of the distances: $x^2+y^2, (x-1)^2+y^2$, and $x^2+((y-1)^2)$. All of these need to be rational, so the differences $2x-1$ and $2 y-1$ are also rational.

The ellipse $3 (x^2+ y^2)-4(x+y)+2 x y==0$ has 193 of the triples (or 386 counting reflections in $y=x$), with inverse points on the cubic $4 (y^3+ x^3)-3 (y^2+ x^2)+2x y ( 2y+ 2x -1)==0$.

So that's the write-up at Rational Distance Problem. Here's more:

Some rational triples have a rational distance to other points. Point (15803760/49193869,38592180/49193869) is also a rational distance from (0,-1). Point (-209/400, 391/300) is also a rational distance from (0,2). Points (209/195, 209/104), (187/280, 31/21), (89/408, 1246/765) are also a rational distance from (1,2).

Many sets of three ore more rational triples are on straight lines. Most of those lines also go through (0,0), (1,0), or (0,1), but not all of them. Are there other equations of order 1, 2, 3, 4 with unexpectedly large numbers of rational points?

The point with the smallest radical to (1,1) seems to be -(2480/8241),11284/24723, at distance $(11023 \sqrt{10})/24723$ with radical 10. The next radical is 17 for point (6/13,45/52).

As of this moment, I've plowed through all the Heronian triangles with longest side 1410000 or less. The available data goes up to 6000000. If anyone has a computer or two with Mathematica that could run my search program for a week or so, let me know and I'll assign you a block to run and some code. Either a solution will be found, or more rational points will be collected.