A few months ago, @Silvia Hao post a topic for Stippling Drawing, we disussed a little bit for robot painting as well. Here I show a small example, so that more members can visualize and play a little bit more with robot painting. There is some gaps between an artifical image to an robot/physical painting.

Robot painting, the method is very simple, only 3 steps.

1. Prepare an image data to robot plot data;

    image = yourImage;
    pts = PixelValuePositions[
       ImageAdjust[ColorQuantize[ColorConvert[image, "Grayscale"], 2]], 0];
    length = Length@pts;
    tour = pts[[FindShortestTour[pts][[2]]]];
    trajectoryData = {2 + #[[1]], -13 + #[[2]], 0} & /@ (0.12*tour);

2. Using robot forward and inverse kinematics;

    InverseSCARA = 
      Compile[{{px, _Real}, {py, _Real}, {pz, _Real}, {\[Alpha], _Real}, \
    {judge, True | False}},
       Module[{L1 = 10, L2 = 7, d4 = 5, c2, s2, c1, 
         s1, \[Theta]1, \[Theta]2, d1, \[Theta]4},
        c2 = (-L1^2 - L2^2 + px^2 + py^2)/(2 L1 L2);
        s2 = If[judge, Sqrt[1 - (c2^2) ], -Sqrt[1 - (c2^2) ]];
        c1 = -((-L1 px - c2 L2 px - s2 L2 py)/(px^2 + py^2));
        s1 = -((s2 L2 px - L1 py - c2 L2 py)/(px^2 + py^2));
        \[Theta]2 = Mod[Simplify[ArcTan[c2, s2]], 2 Pi] + Pi;
        \[Theta]1 = Mod[Simplify[ArcTan[c1, s1]], 2 Pi];
        d1 = pz + d4;
        \[Theta]4 = Mod[\[Theta]1 + \[Theta]2 - \[Alpha], 2 Pi];
        {d1, \[Theta]1, \[Theta]2, \[Theta]4}]];

3. Manipulate a robot and feed data for robot trajectory. I use FindShortTour as quick way to convert point to a tour. The painting style is few, only two ways (point and lines) so far.

Below robot's self-portrait is interesting, does have some Nest sense.

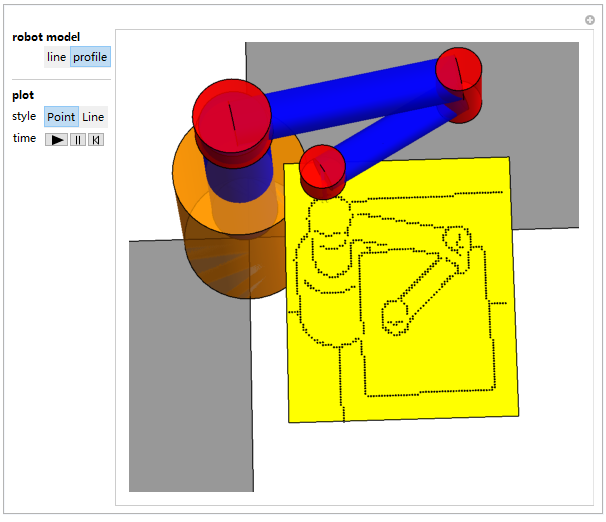
Attached is a demonstration file for playing:

Attachments: