Any forecast of this behavior - which is ratio of vertex number of happy and unhappy?

gfun[n_] := Graph[# <-> Total[IntegerDigits[#]^2] & /@ Range[n]]

data = ParallelTable[N[Divide @@ (Length /@ ConnectedComponents[gfun[k]])], {k, 500, 10000}];

ListLinePlot[data, PlotTheme -> "Detailed", AspectRatio -> 1/4, PlotRange -> All]

Maybe not a constant but it does appear to be approaching a simple function as it approaches infinity, maybe linear or maybe a logarithmic.

A spectral image of the FFT of this series may be interesting.

I think Marco nailed it in terms of code compactness. I suggest, which seems stable layout-wise, invariant of Range[x] - and what does that mean actually?

Graph[# <-> Total[IntegerDigits[#]^2] & /@ Range[1000],
 GraphLayout -> "RadialEmbedding", GraphStyle -> "LargeNetwork", 
 VertexLabels -> Placed["Name", Tooltip]]

Hi,

It is by the way indeed interesting to use graphs to visualise this:

Graph[# -> Total[IntegerDigits[#]^2] & /@ Range[10000]]

It turns out that there is a skeleton that is relatively stable.

GraphPlot[# -> Total[IntegerDigits[#]^2] & /@ Range[1000], Method -> "CircularEmbedding"]

and this

GraphPlot[# -> Total[IntegerDigits[#]^2] & /@ Range[200], Method -> "LinearEmbedding"]

look pretty, too, and have a meaning. I think, however, that the Layered Graph is the best visualisation:

LayeredGraphPlot[# -> Total[IntegerDigits[#]^2] & /@ Range[200]]

The upper graph contains the sad numbers and the lower one the happy ones. This also explains why you always reach one out of nine numbers. The lower graph has a fixed point. You always get to "1" and then stay there - that's happy. If you carefully look at the other graph you see that there is a cycle of eight vertices.

If you want to see that cycle you can use:

g = Graph[# -> Total[IntegerDigits[#]^2] & /@ Range[1000]];
cycle=FindCycle[g]
(*{{4 -> 16, 16 -> 37, 37-> 58, 58-> 89, 89-> 145, 145 -> 42, 42-> 20, 20-> 4}}*)

This can be used to highlight the subgraph:

HighlightGraph[g, cycle]

If you compare that to the table of my first reply all numbers are accounted for.

Cheers,

Marco

Perhaps use the following code:

GraphPlot[
 Rule @@@ DeleteDuplicates[
   Partition[NestList[Total[IntegerDigits[#]^2] &, 4, 99], 2, 1]
   ]
]

Depending on the version you have you can use Subsequences[...,{2}] rather than Partition[...,2,1], Also you could probably use FindTransientRepeat in a nice way.

I'm not sure if I understand your question. But using ToString, Characters and ToExpression is definitely not fast, using IntegerDigits should be much much faster!

Hi there,

this is actually quite nice. Here is a function that generates the lists.

f[start_] := Module[{list = {start}}, NestWhileList[Total[IntegerDigits[#]^2] &, start, Unequal, All]]

We can now generate that for the first, say 100 integers:

Table[f[k][[-1]], {k, 1, 100}]

The ones indicate happy numbers - all the others are sad. The interesting bit is that the sequences only reach one out of nine numbers:

Histogram[Table[f[k][[-1]], {k, 1, 100000}], 200]

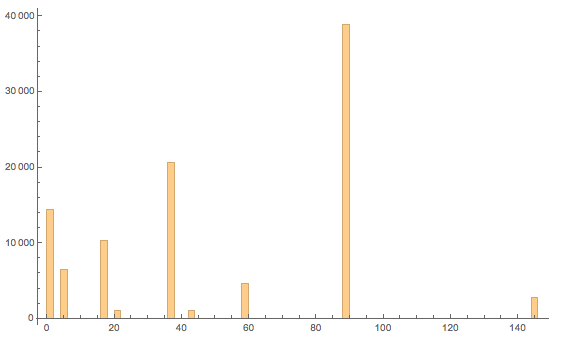
or

Tally[Table[f[k][[-1]], {k, 1, 100000}]] //TableForm

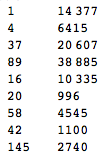
This table show the approximate relative frequencies of the terminal numbers.

This here reveals little of a pattern:

Partition[Table[f[k][[-1]], {k, 1, 1600}] /. {x_ /; x != 1 -> 0}, 40] // ArrayPlot

You can also play with this:

Manipulate[Partition[Table[f[k][[-1]], {k, 1, 1600}] /. {x_ /; x != 1 -> 0}, UpTo[j]] // ArrayPlot, {j, 5, 80, 1}]

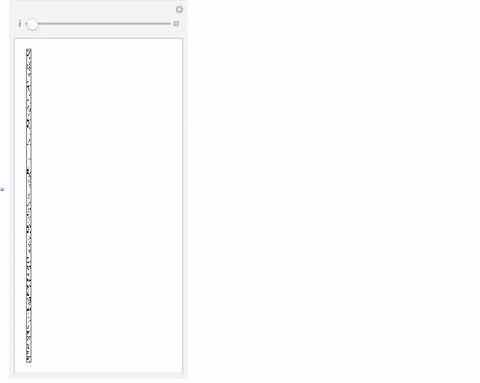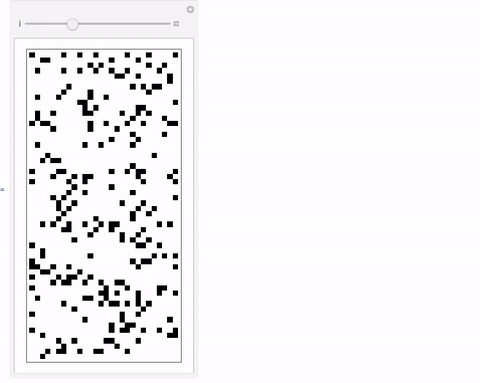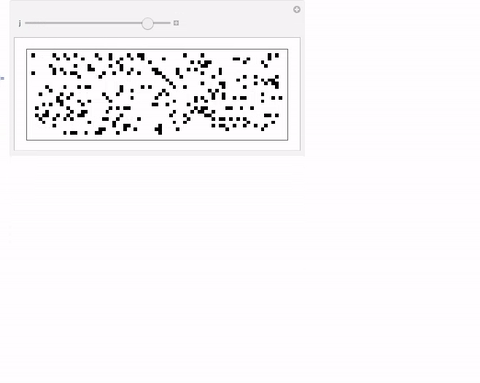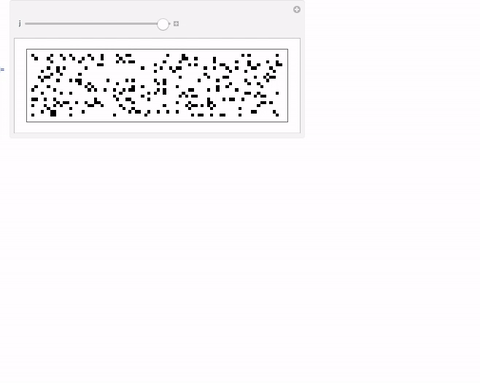
Cheers,

Marco