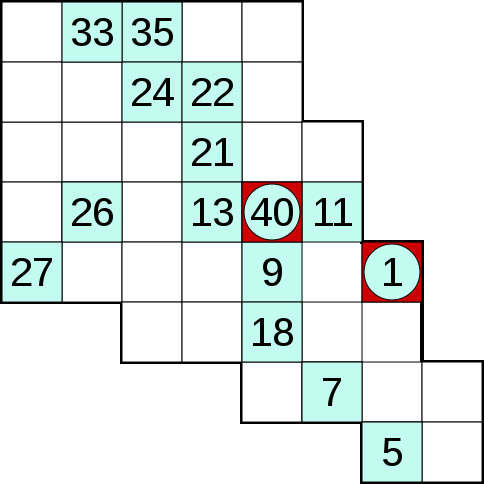
You probably have seen the Hidato puzzles in magazines, newspapers or online. The goal of the puzzle game is to fill a grid with numbers such that consecutive number are adjacent to each other. There are a number of varieties of the game: namely the different kind of grids used: square ('Hidato' or 'Numbrix') or hexagonal ('Beehive' or sometimes called 'Hex'), and the 'connectivity' of the grid: for square grid it can connect horizontally and vertically ('Numbrix') or horizontally, vertically, and diagonally ('Hidato'). Generally the begin and end points are already filled in, along with some hints. For example:
Let' s start with defining the kind of game we are playing, I will support the above mentioned 3 types of games, along with the synonyms:
$HidatoMode = "Hidato";(*"Hidato" "Hex" "Beehive" "Numbrix" *)
To make a solver we are going to consider all the possible candidates that can fit in each cell, by using logic we will be able to cross out certain candidates for each cell. We will keep a list of cells (in cartesian coordinates) and a list of candidates for each cell. Using these two lists we can solve a Hidato puzzle. We will try to solve the above puzzle, so let's start by setting up the cells and candidates (cands) variables:
cells={{1,4},{1,5},{1,6},{1,7},{1,8},{2,4},{2,5},{2,6},{2,7},{2,8},{3,3},{3,4},{3,5},{3,6},{3,7},{3,8},{4,3},{4,4},{4,5},{4,6},{4,7},{4,8},{5,2},{5,3},{5,4},{5,5},{5,6},{5,7},{5,8},{6,2},{6,3},{6,4},{6,5},{6,6},{7,1},{7,2},{7,3},{7,4},{8,1},{8,2}}; (* cartesian coordinates of the cells *)
candidates=ConstantArray[Range@Length[cells],Length[cells]]; (* all the cells start with candidates 1 through 40 *)
hints={
{{1,4},{27}},
{{2,5},{26}},
{{7,1},{5}},
{{6,2},{7}},
{{5,3},{18}},
{{5,4},{9}},
{{5,5},{40}},
{{6,5},{11}},
{{4,5},{13}},
{{4,6},{21}},
{{4,7},{22}},
{{3,7},{24}},
{{3,8},{35}},
{{2,8},{33}},
{{7,4},{1}}
}; (* these are the hints which is a list of coordinates with the candidates that are possible for that cell (just one candidate because they are given) *)
indices=Flatten[Position[cells,#]&/@hints[[All,1]]]; (* find the indices of these cells *)
candidates[[indices]]=hints[[All,2]]; (* replace the candidates in the candidates list *)
Let's make a function to visualize it:
VisualizeHidato[cells_List, cands_List] := Module[{grid, nums, cb, hx},
Switch[$HidatoMode, "Hidato" | "Numbrix",
grid = {EdgeForm[Thick],
MapThread[
If[Length[#2] > 1, {FaceForm[],
Rectangle[#1]}, {FaceForm[LightGray],
Rectangle[#1]}] &, {cells, cands}]};
nums =
MapThread[
If[Length[#1] == 1, Text[Style[First[#1], 16], #2 + 0.5 {1, 1}],
Text[Tooltip[Style[Length[#1], Red, 10], #1], #2 +
0.5 {1, 1}]] &, {cands, cells}];
cb = CoordinateBounds[cells];
Graphics[{grid, nums},
PlotRange -> cb + {{-0.5, 1.5}, {-0.5, 1.5}},
ImageSize -> 60 (1 + cb[[1, 2]] - cb[[1, 1]])]
,
"Hex" | "Beehive",
hx = {{1, 1/2}, {0, Sqrt[3]/2}};
grid = {EdgeForm[Thick],
MapThread[
If[Length[#2] > 1, {FaceForm[],
RegularPolygon[hx.#1, {1/Sqrt[3.0], \[Pi]/6}, 6]}, {FaceForm[
LightGray],
RegularPolygon[hx.#1, {1/Sqrt[3.0], \[Pi]/6}, 6]}] &, {cells,
cands}]};
nums =
MapThread[
If[Length[#1] == 1, Text[Style[First[#1], 16], hx.#2],
Text[Tooltip[Style[Length[#1], Red, 10], #1],
hx.#2]] &, {cands, cells}];
cb = CoordinateBounds[(hx.#) & /@ cells];
Graphics[{grid, nums}, PlotRange -> cb + {{-1, 1}, {-1, 1}},
ImageSize -> 35 (1 + cb[[1, 2]] - cb[[1, 1]])]
,
_,
Print["Incorrect $HidatoMode: ", $HidatoMode];
Abort[];
]
]
VisualizeHidato[cells, candidates]
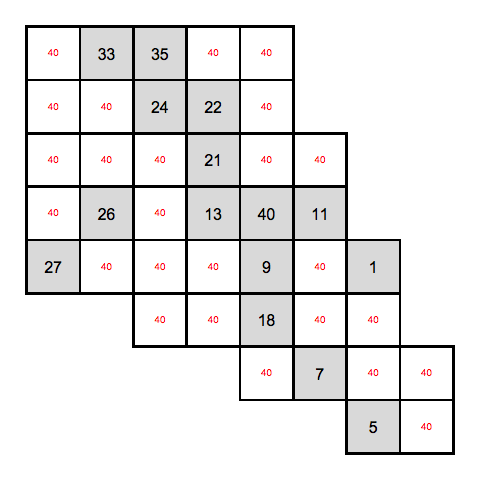
Here the red number is the number of candidates are left for that cell (a tooltip will be shown when you hover over, showing the candidates). Gray cells are the ones that are 'solved'.
Now we have to add some logic in order to solve the puzzle. First the simplest technique will just look at the distance to a certain given cell. If a given cell is e.g. 15, then a cell 3 away, can never contain 14 because 14 must be a neighbour of 15. This can be implemented as:
NeighbourQ[cell1_, cell2_] := (CellDistance[cell1, cell2] === 1)
CellDistance[cell1_, cell2_] := Module[{dx, dy},
Switch[$HidatoMode, "Hidato",
ChessboardDistance[cell1, cell2]
,
"Hex" | "Beehive",
{dx, dy} = cell1 - cell2;
If[Sign[dx] == Sign[dy], Abs[dx + dy], Max[Abs[dx], Abs[dy]]]
,
"Numbrix",
ManhattanDistance[cell1, cell2]
,
_,
Print["Incorrect $HidatoMode: ", $HidatoMode];
Abort[];
]
]
GrowNeighbours[neighbours_, set_List] :=
Module[{lastdone, ids, newneighbours, old},
old = Join @@ set[[All, All, 1]];
lastdone = Last[set];
ids = lastdone[[All, 1]];
newneighbours = Union @@ (neighbours /@ ids);
newneighbours = Complement[newneighbours, old]; (*only new ones*)
If[Length[newneighbours] > 0,
Append[set, Thread[{newneighbours, lastdone[[1, 2]] + 1}]]
,
set
]
]
ReachDelete[cells_List, cands_List, neighbours_, startid_] :=
Module[{seed, distances, val, newcands},
If[MatchQ[cands[[startid]], {_}],
val = cands[[startid, 1]];
seed = {{{startid, 0}}};
distances =
Join @@ FixedPoint[GrowNeighbours[neighbours, #] &, seed];
If[Length[distances] > 0,
distances = Select[distances, Last[#] > 0 &];
If[Length[distances] > 0,
newcands = cands;
distances[[All, 2]] =
Transpose[
val + Outer[Times, {-1, 1}, distances[[All, 2]] - 1]];
Do[newcands[[\[CurlyPhi][[1]]]] =
Complement[newcands[[\[CurlyPhi][[1]]]],
Range @@ \[CurlyPhi][[2]]];
, {\[CurlyPhi], distances}
];
newcands
,
cands
]
,
cands
]
,
Echo[cands[[startid]], "cands"];
Print["invalid starting point for neighbour search: ", startid];
Abort[];
]
]
GapSearch[cells_List, cands_List] :=
Module[{givensid, givens, neighbours},
givensid = Flatten[Position[cands, {_}]];
givens = {cells[[givensid]], givensid,
Flatten[cands[[givensid]]]}\[Transpose];
If[Length[givens] > 0,
givens = SortBy[givens, Last];
givens = Split[givens, Last[#2] == Last[#1] + 1 &];
givens = If[Length[#] <= 2, #, #[[{1, -1}]]] & /@ givens;
If[Length[givens] > 0,
givens = Join @@ givens;
If[Length[givens] > 0,
neighbours = Outer[NeighbourQ, cells, cells, 1];
neighbours =
Association[
MapIndexed[First[#2] -> Flatten[Position[#1, True]] &,
neighbours]];
givens = givens[[All, 2]];
Fold[ReachDelete[cells, #1, neighbours, #2] &, cands, givens]
,
cands
]
,
cands
]
,
cands
]
]
Now we can make a Solve function that iteratively applies this technique:
HidatoSolve[cells_List, cands_List] :=
Module[{newcands = cands, old},
Print@VisualizeHidato[cells, newcands];
old = -1;
While[old =!= newcands,
old = newcands;
newcands = GapSearch[cells, newcands];
];
Print@VisualizeHidato[cells, newcands];
newcands
]
HidatoSolve[cells, candidates];
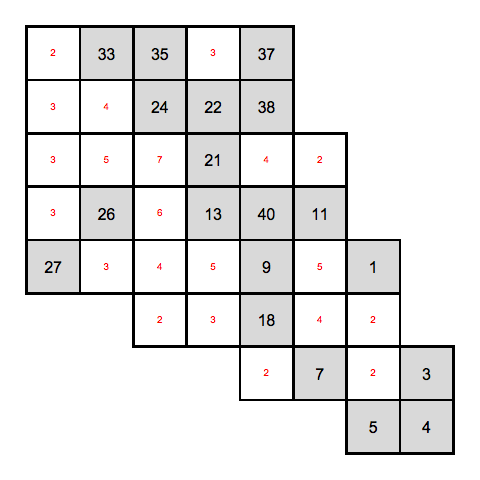
just by this techniques we solved 4 cells, and the number of candidates drop from 40 to 2--7.
We will now use some techniques borrowed from Sudoku puzzles. Namely, we will use Hidden Singles/Pairs/Triples/Quads etc and Naked Singles/Pairs/Triples/Quads etc (Hidden and Naked Subsets in general). The basic idea behind the former is: if n candidates only appear in n cells, than we can eliminate all the other candidates from these n cells. Naked subsets has the following logic: if n cells only have n distinct candidates, then we can delete these candidates from all the other cells.
Here are the implementations:
HiddenSingle[cands_List] := Module[{singles, newcands = cands},
singles = Cases[Tally[Flatten[cands]], {_, 1}];
If[Length[singles] > 0,
singles = Sort[singles[[All, 1]]];
newcands =
If[ContainsAny[#, singles], Intersection[#, singles], #] & /@
newcands;
newcands
,
cands
]
]
HiddenN[cands_List, n_Integer?(# > 1 &)] := Module[{tmp, out},
tmp = cands;
tmp = Join @@ MapIndexed[{#1, First[#2]} &, tmp, {2}];
tmp = Transpose /@ GatherBy[tmp, First];
tmp[[All, 1]] = tmp[[All, 1, 1]];
tmp = Select[tmp, 2 <= Length[Last[#]] <= n &];
If[Length[tmp] > 0,
tmp = Transpose /@ Subsets[tmp, {n}];
tmp[[All, 2]] = Union @@@ tmp[[All, 2]];
tmp = Select[tmp, Length[Last[#]] == n &];
If[Length[tmp] > 0,
(* for each tmp {cands,
cells} in each of the cells delete everything except the cands *)
out = cands;
Do[
Do[
out[[c]] = Select[out[[c]], MemberQ[t[[1]], #] &];
,
{c, t[[2]]}
]
,
{t, tmp}
];
out
,
cands
]
,
cands
]
]
NakedN[cands_List, n_Integer?(# > 1 &)] := Module[{tmp, newcands, ids},
tmp = {Range[Length[cands]], cands}\[Transpose];
tmp = Select[tmp, 2 <= Length[Last[#]] <= n &];
If[Length[tmp] > 0,
tmp = Transpose /@ Subsets[tmp, {n}];
tmp[[All, 2]] = Union @@@ tmp[[All, 2]];
tmp = Select[tmp, Length[Last[#]] == n &];
If[Length[tmp] > 0,
newcands = cands;
Do[
ids = Complement[Range[Length[newcands]], t[[1]]];
newcands[[ids]] =
DeleteCases[newcands[[ids]],
Alternatives @@ t[[2]], \[Infinity]];
,
{t, tmp}
];
newcands
,
cands
]
,
cands
]
]
And our updated solve routine (i went up to 8 for hidden and naked subsets):
HidatoSolve[cells_List, cands_List] :=
Module[{newcands = cands, old},
Print@VisualizeHidato[cells, newcands];
old = -1;
While[old =!= newcands,
old = newcands;
newcands = GapSearch[cells, newcands];
If[old === newcands,
newcands = HiddenSingle[newcands];
If[old === newcands,
newcands = NakedN[newcands, 2];
newcands = HiddenN[newcands, 2];
If[old === newcands,
newcands = NakedN[newcands, 3];
newcands = HiddenN[newcands, 3];
If[old === newcands,
newcands = NakedN[newcands, 4];
newcands = HiddenN[newcands, 4];
If[old === newcands,
newcands = NakedN[newcands, 5];
newcands = HiddenN[newcands, 5];
If[old === newcands,
newcands = NakedN[newcands, 6];
newcands = HiddenN[newcands, 6];
If[old === newcands,
newcands = NakedN[newcands, 7];
newcands = HiddenN[newcands, 7];
If[old === newcands,
newcands = NakedN[newcands, 8];
newcands = HiddenN[newcands, 8];
]
]
]
]
]
]
]
]
];
Print@VisualizeHidato[cells, newcands];
newcands
]
HidatoSolve[cells, candidates];
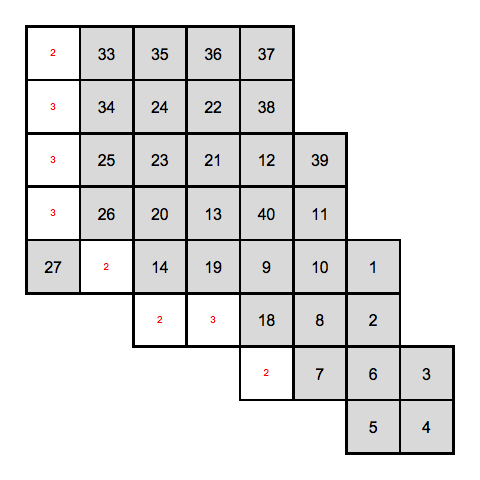
We solved even more cells, and reduced the number of candidates even more! We are now left with 8 unsolved cells with only either 2 or 3 candidates. In order to solve the last cells we have to use some advanced techniques like Cornering. Which I implemented below. In addition, I have implement a depth-first brute force solution finder. The basic idea is: start at cell with candidate 1. Iterate over the neighbours that have 2 as a candidates. For each of them iterate over neighbours that have 3 as candidate, et cetera. If a certain cell with candidate n does not a neighbouring cell with candidate n+1, the search branch is stopped there. If we reach the final cell, then we have a solution (and possibly we can find multiple solutions). The total final code is:
ClearAll[NeighbourQ, CellDistance, VisualizeHidato, HiddenSingle, NakedN, HiddenN, ChainSearch, HidatoSolve, Cornering, ValidPuzzle, GapSearch, ReachDelete, GrowNeighbours]
$HidatoMode = {"Hidato", "Hex", "Beehive", "Numbrix"}[[1]];
NeighbourQ[cell1_, cell2_] := (CellDistance[cell1, cell2] === 1)
ValidPuzzle[cells_List, cands_List] :=
MemberQ[cands, {1}] \[And] MemberQ[cands, {Length[cells]}] \[And]
Length[cells] == Length[candidates] \[And]
MinMax[Flatten[cands]] === {1,
Length[cells]} \[And] (Union @@ cands === Range[Length[cells]])
CellDistance[cell1_, cell2_] := Module[{dx, dy},
Switch[$HidatoMode, "Hidato",
ChessboardDistance[cell1, cell2]
,
"Hex" | "Beehive",
{dx, dy} = cell1 - cell2;
If[Sign[dx] == Sign[dy], Abs[dx + dy], Max[Abs[dx], Abs[dy]]]
,
"Numbrix",
ManhattanDistance[cell1, cell2]
,
_,
Print["Incorrect $HidatoMode: ", $HidatoMode];
Abort[];
]
]
VisualizeHidato[cells_List, cands_List] := Module[{grid, nums, cb, hx},
Switch[$HidatoMode, "Hidato" | "Numbrix",
grid = {EdgeForm[Thick],
MapThread[
If[Length[#2] > 1, {FaceForm[],
Rectangle[#1]}, {FaceForm[LightGray],
Rectangle[#1]}] &, {cells, cands}]};
nums =
MapThread[
If[Length[#1] == 1, Text[Style[First[#1], 16], #2 + 0.5 {1, 1}],
Text[Tooltip[Style[Length[#1], Red, 10], #1], #2 +
0.5 {1, 1}]] &, {cands, cells}];
cb = CoordinateBounds[cells];
Graphics[{grid, nums},
PlotRange -> cb + {{-0.5, 1.5}, {-0.5, 1.5}},
ImageSize -> 60 (1 + cb[[1, 2]] - cb[[1, 1]])]
,
"Hex" | "Beehive",
hx = {{1, 1/2}, {0, Sqrt[3]/2}};
grid = {EdgeForm[Thick],
MapThread[
If[Length[#2] > 1, {FaceForm[],
RegularPolygon[hx.#1, {1/Sqrt[3.0], \[Pi]/6}, 6]}, {FaceForm[
LightGray],
RegularPolygon[hx.#1, {1/Sqrt[3.0], \[Pi]/6}, 6]}] &, {cells,
cands}]};
nums =
MapThread[
If[Length[#1] == 1, Text[Style[First[#1], 16], hx.#2],
Text[Tooltip[Style[Length[#1], Red, 10], #1],
hx.#2]] &, {cands, cells}];
cb = CoordinateBounds[(hx.#) & /@ cells];
Graphics[{grid, nums}, PlotRange -> cb + {{-1, 1}, {-1, 1}},
ImageSize -> 35 (1 + cb[[1, 2]] - cb[[1, 1]])]
,
_,
Print["Incorrect $HidatoMode: ", $HidatoMode];
Abort[];
]
]
HiddenSingle[cands_List] := Module[{singles, newcands = cands},
singles = Cases[Tally[Flatten[cands]], {_, 1}];
If[Length[singles] > 0,
singles = Sort[singles[[All, 1]]];
newcands =
If[ContainsAny[#, singles], Intersection[#, singles], #] & /@
newcands;
newcands
,
cands
]
]
HiddenN[cands_List, n_Integer?(# > 1 &)] := Module[{tmp, out},
tmp = cands;
tmp = Join @@ MapIndexed[{#1, First[#2]} &, tmp, {2}];
tmp = Transpose /@ GatherBy[tmp, First];
tmp[[All, 1]] = tmp[[All, 1, 1]];
tmp = Select[tmp, 2 <= Length[Last[#]] <= n &];
If[Length[tmp] > 0,
tmp = Transpose /@ Subsets[tmp, {n}];
tmp[[All, 2]] = Union @@@ tmp[[All, 2]];
tmp = Select[tmp, Length[Last[#]] == n &];
If[Length[tmp] > 0,
(* for each tmp {cands,
cells} in each of the cells delete everything except the cands *)
out = cands;
Do[
Do[
out[[c]] = Select[out[[c]], MemberQ[t[[1]], #] &];
,
{c, t[[2]]}
]
,
{t, tmp}
];
out
,
cands
]
,
cands
]
]
NakedN[cands_List, n_Integer?(# > 1 &)] := Module[{tmp, newcands, ids},
tmp = {Range[Length[cands]], cands}\[Transpose];
tmp = Select[tmp, 2 <= Length[Last[#]] <= n &];
If[Length[tmp] > 0,
tmp = Transpose /@ Subsets[tmp, {n}];
tmp[[All, 2]] = Union @@@ tmp[[All, 2]];
tmp = Select[tmp, Length[Last[#]] == n &];
If[Length[tmp] > 0,
newcands = cands;
Do[
ids = Complement[Range[Length[newcands]], t[[1]]];
newcands[[ids]] =
DeleteCases[newcands[[ids]],
Alternatives @@ t[[2]], \[Infinity]];
,
{t, tmp}
];
newcands
,
cands
]
,
cands
]
]
Cornering[cells_List, cands_List] :=
Module[{newcands, neighbours, filled, neighboursfiltered, cellid,
filledneighours, begin, end, beginend},
filled = Flatten[MapIndexed[If[Length[#1] == 1, #2, {}] &, cands]];
begin = If[MemberQ[cands, {1}], {}, {1}];
end = If[MemberQ[cands, {Length[cells]}], {}, {Length[cells]}];
beginend = Join[begin, end];
neighbours = Outer[NeighbourQ, cells, cells, 1];
neighbours =
Association[
MapIndexed[
First[#2] -> {Complement[Flatten[Position[#1, True]], filled],
Intersection[Flatten[Position[#1, True]], filled]} &,
neighbours]];
KeyDropFrom[neighbours, filled];
neighbours = Select[neighbours, Length[First[#]] == 1 &];
If[Length[neighbours] > 0,
newcands = cands;
neighbours = KeyValueMap[List, neighbours];
Do[
cellid = n[[1]];
filledneighours = n[[2, 2]];
filledneighours = Join @@ cands[[filledneighours]];
filledneighours =
Union[filledneighours - 1, filledneighours + 1];
filledneighours = Union[filledneighours, beginend];
newcands[[cellid]] =
Intersection[newcands[[cellid]], filledneighours];
,
{n, neighbours}
];
newcands
,
cands
]
]
ChainSearch[cells_, cands_] := Module[{neighbours, sols, out},
neighbours = Outer[NeighbourQ, cells, cells, 1];
neighbours =
Association[
MapIndexed[First[#2] -> Flatten[Position[#1, True]] &,
neighbours]];
sols = Reap[ChainSearch[neighbours, cands, {}];][[2]];
If[Length[sols] > 0,
sols = sols[[1]];
If[Length[sols] > 1,
Print["multiple solutions found, showing first"];
];
sols = First[sols];
out = cands;
out[[sols]] = List /@ Range[Length[out]];
out
,
cands
]
]
ChainSearch[neighbours_, cands_List, solcellids_List] :=
Module[{largest, largestid, next, poss},
largest = Length[solcellids];
largestid = Last[solcellids, 0];
If[largest < Length[cands],
next = largest + 1;
poss =
Flatten[MapIndexed[If[MemberQ[#1, next], First[#2], {}] &, cands]];
If[Length[poss] > 0,
If[largest > 0,
poss = Intersection[poss, neighbours[largestid]];
];
poss = Complement[poss, solcellids]; (* can't be in previous path*)
If[Length[poss] > 0, (* there are 'next' ones iterate over,
calling this function *)
Do[
ChainSearch[neighbours, cands, Append[solcellids, p]]
,
{p, poss}
]
]
,
Print["There should be a next!"];
Abort[];
]
,
Sow[solcellids] (*
we found a solution with this ordering of cells *)
]
]
GrowNeighbours[neighbours_, set_List] :=
Module[{lastdone, ids, newneighbours, old},
old = Join @@ set[[All, All, 1]];
lastdone = Last[set];
ids = lastdone[[All, 1]];
newneighbours = Union @@ (neighbours /@ ids);
newneighbours = Complement[newneighbours, old]; (*only new ones*)
If[Length[newneighbours] > 0,
Append[set, Thread[{newneighbours, lastdone[[1, 2]] + 1}]]
,
set
]
]
ReachDelete[cells_List, cands_List, neighbours_, startid_] :=
Module[{seed, distances, val, newcands},
If[MatchQ[cands[[startid]], {_}],
val = cands[[startid, 1]];
seed = {{{startid, 0}}};
distances =
Join @@ FixedPoint[GrowNeighbours[neighbours, #] &, seed];
If[Length[distances] > 0,
distances = Select[distances, Last[#] > 0 &];
If[Length[distances] > 0,
newcands = cands;
distances[[All, 2]] =
Transpose[
val + Outer[Times, {-1, 1}, distances[[All, 2]] - 1]];
Do[newcands[[\[CurlyPhi][[1]]]] =
Complement[newcands[[\[CurlyPhi][[1]]]],
Range @@ \[CurlyPhi][[2]]];
, {\[CurlyPhi], distances}
];
newcands
,
cands
]
,
cands
]
,
Print["invalid starting point for neighbour search"];
Abort[];
]
]
GapSearch[cells_List, cands_List] :=
Module[{givensid, givens, neighbours},
givensid = Flatten[Position[cands, {_}]];
givens = {cells[[givensid]], givensid,
Flatten[cands[[givensid]]]}\[Transpose];
If[Length[givens] > 0,
givens = SortBy[givens, Last];
givens = Split[givens, Last[#2] == Last[#1] + 1 &];
givens = If[Length[#] <= 2, #, #[[{1, -1}]]] & /@ givens;
If[Length[givens] > 0,
givens = Join @@ givens;
If[Length[givens] > 0,
neighbours = Outer[NeighbourQ, cells, cells, 1];
neighbours =
Association[
MapIndexed[First[#2] -> Flatten[Position[#1, True]] &,
neighbours]];
givens = givens[[All, 2]];
Fold[ReachDelete[cells, #1, neighbours, #2] &, cands, givens]
,
cands
]
,
cands
]
,
cands
]
]
HidatoSolve[cells_List, cands_List] :=
Module[{newcands = cands, old},
Print@VisualizeHidato[cells, newcands];
If[ValidPuzzle[cells, cands] \[Or] 1 == 1,
old = -1;
newcands = GapSearch[cells, newcands];
While[old =!= newcands,
old = newcands;
newcands = GapSearch[cells, newcands];
If[old === newcands,
newcands = HiddenSingle[newcands];
If[old === newcands,
newcands = NakedN[newcands, 2];
newcands = HiddenN[newcands, 2];
If[old === newcands,
newcands = NakedN[newcands, 3];
newcands = HiddenN[newcands, 3];
If[old === newcands,
newcands = Cornering[cells, newcands];
If[old === newcands,
newcands = NakedN[newcands, 4];
newcands = HiddenN[newcands, 4];
If[old === newcands,
newcands = NakedN[newcands, 5];
newcands = HiddenN[newcands, 5];
If[old === newcands,
newcands = NakedN[newcands, 6];
newcands = HiddenN[newcands, 6];
If[old === newcands,
newcands = NakedN[newcands, 7];
newcands = HiddenN[newcands, 7];
If[old === newcands,
newcands = NakedN[newcands, 8];
newcands = HiddenN[newcands, 8];
]
]
]
]
]
]
]
]
]
];
If[Length[Flatten[newcands]] > Length[newcands], (*
if not solved do a depth-first brute force search*)
newcands = ChainSearch[cells, newcands];
];
Print@VisualizeHidato[cells, newcands];
newcands
,
Print["There seems to be something wrong with your Hidato puzzle. Check if the cells and candidates have the same length, all the numbers are among the candidates \[Ellipsis]"]
]
]
We can now call the function and solve the puzzle:
cells = {{1, 4}, {1, 5}, {1, 6}, {1, 7}, {1, 8}, {2, 4}, {2, 5}, {2,
6}, {2, 7}, {2, 8}, {3, 3}, {3, 4}, {3, 5}, {3, 6}, {3, 7}, {3,
8}, {4, 3}, {4, 4}, {4, 5}, {4, 6}, {4, 7}, {4, 8}, {5, 2}, {5,
3}, {5, 4}, {5, 5}, {5, 6}, {5, 7}, {5, 8}, {6, 2}, {6, 3}, {6,
4}, {6, 5}, {6, 6}, {7, 1}, {7, 2}, {7, 3}, {7, 4}, {8, 1}, {8,
2}}; (* cartesian coordinates of the cells *)
candidates =
ConstantArray[Range@Length[cells],
Length[cells]]; (* all the cells start with candidates 1 through \
40 *)
hints = {
{{1, 4}, {27}},
{{2, 5}, {26}},
{{7, 1}, {5}},
{{6, 2}, {7}},
{{5, 3}, {18}},
{{5, 4}, {9}},
{{5, 5}, {40}},
{{6, 5}, {11}},
{{4, 5}, {13}},
{{4, 6}, {21}},
{{4, 7}, {22}},
{{3, 7}, {24}},
{{3, 8}, {35}},
{{2, 8}, {33}},
{{7, 4}, {1}}
}; (* these are the hints which is a list of coordinates with the \
candidates that are possible for that cell (just one candidate \
because they are given) *)
indices =
Flatten[Position[cells, #] & /@
hints[[All, 1]]]; (* find the indices of these cells *)
candidates[[indices]] =
hints[[All, 2]]; (* replace the candidates in the candidates list *)
out = HidatoSolve[cells, candidates];
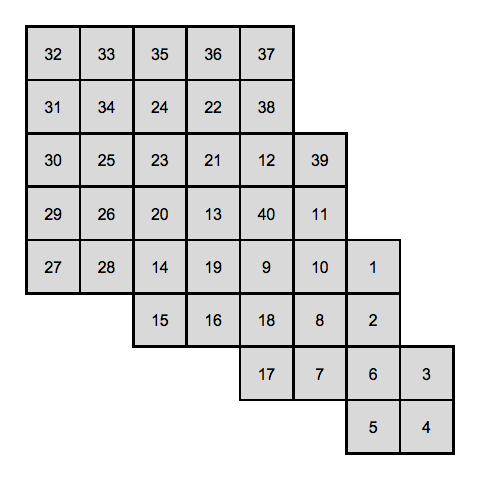
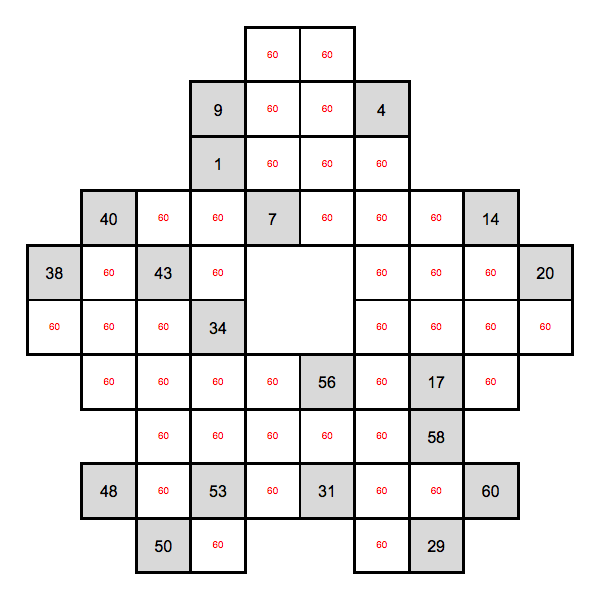
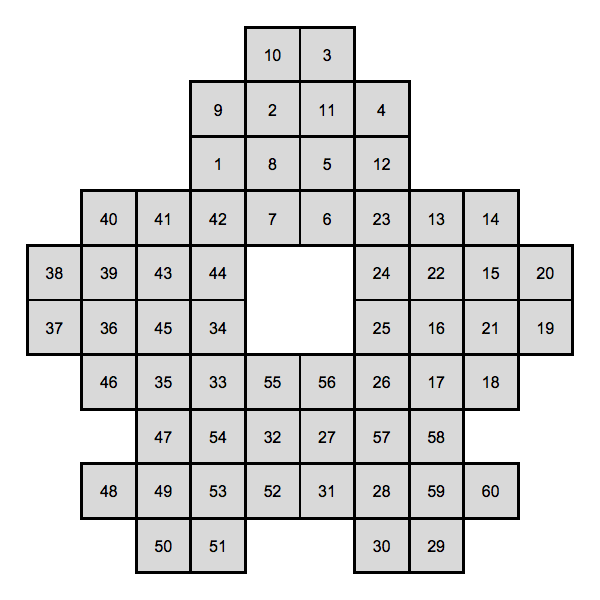
And it works on puzzles with holes in it too:
$HidatoMode = "Hidato";
cells = {{5, 10}, {6, 10}, {4, 9}, {5, 9}, {6, 9}, {7, 9}, {4, 8}, {5,
8}, {6, 8}, {7, 8}, {2, 7}, {3, 7}, {4, 7}, {5, 7}, {6, 7}, {7,
7}, {8, 7}, {9, 7}, {1, 6}, {2, 6}, {3, 6}, {4, 6}, {7, 6}, {8,
6}, {9, 6}, {10, 6}, {1, 5}, {2, 5}, {3, 5}, {4, 5}, {7, 5}, {8,
5}, {9, 5}, {10, 5}, {2, 4}, {3, 4}, {4, 4}, {5, 4}, {6, 4}, {7,
4}, {8, 4}, {9, 4}, {3, 3}, {4, 3}, {5, 3}, {6, 3}, {7, 3}, {8,
3}, {2, 2}, {3, 2}, {4, 2}, {5, 2}, {6, 2}, {7, 2}, {8, 2}, {9,
2}, {3, 1}, {4, 1}, {7, 1}, {8, 1}};
candidates = ConstantArray[Range@Length[cells], Length[cells]];
hints = {
{{4, 8}, {1}},
{{9, 2}, {60}},
{{2, 2}, {48}},
{{9, 7}, {14}},
{{2, 7}, {40}},
{{1, 6}, {38}},
{{8, 1}, {29}},
{{7, 9}, {4}},
{{4, 9}, {9}},
{{3, 1}, {50}},
{{4, 2}, {53}},
{{6, 2}, {31}},
{{6, 4}, {56}},
{{8, 3}, {58}},
{{8, 4}, {17}},
{{4, 5}, {34}},
{{3, 6}, {43}},
{{5, 7}, {7}},
{{10, 6}, {20}}
};
indices = Flatten[Position[cells, #] & /@ hints[[All, 1]]];
candidates[[indices]] = hints[[All, 2]];
out = HidatoSolve[cells, candidates];
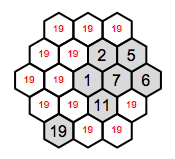
Or the hexagonal (beehive) variant:
$HidatoMode = "Hex";
cells = Join @@ {{#, 1} & /@ Range[3], {#, 2} & /@
Range[0, 3], {#, 3} & /@ Range[-1, 3], {#, 4} & /@
Range[-1, 2], {#, 5} & /@ Range[-1, 1]};
candidates = ConstantArray[Range@Length[cells], Length[cells]];
hints = {
{{1, 1}, {19}},
{{1, 3}, {1}},
{{1, 4}, {2}},
{{2, 2}, {11}},
{{2, 3}, {7}},
{{2, 4}, {5}},
{{3, 3}, {6}}
};
indices = Flatten[Position[cells, #] & /@ hints[[All, 1]]];
candidates[[indices]] = hints[[All, 2]];
out = HidatoSolve[cells, candidates];
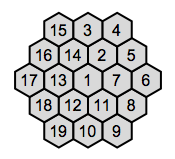
Or bigger puzzles:
$HidatoMode = "Hex";
cells = Join @@ {
{#, 1} & /@ Range[6], {#, 2} & /@ Range[0, 6], {#, 3} & /@
Range[-1, 6], {#, 4} & /@ Range[-2, 6], {#, 5} & /@
Range[-3, 6], {#, 6} & /@
Join[Range[-4, 0], Range[2, 6]], {#, 7} & /@
Range[-4, 5], {#, 8} & /@ Range[-4, 4], {#, 9} & /@
Range[-4, 3], {#, 10} & /@ Range[-4, 2], {#, 11} & /@ Range[-4, 1]
};
candidates = ConstantArray[Range@Length[cells], Length[cells]];
hints = {
{{1, 1}, {32}},
{{1, 3}, {36}},
{{1, 10}, {62}},
{{2, 3}, {37}},
{{2, 4}, {77}},
{{2, 6}, {79}},
{{3, 2}, {39}},
{{3, 3}, {87}},
{{3, 9}, {60}},
{{4, 2}, {89}},
{{4, 5}, {84}},
{{4, 6}, {83}},
{{4, 8}, {59}},
{{5, 2}, {90}},
{{5, 4}, {48}},
{{5, 6}, {51}},
{{6, 6}, {53}},
{{0, 2}, {31}},
{{0, 5}, {25}},
{{0, 6}, {75}},
{{0, 9}, {1}},
{{-1, 5}, {22}},
{{-1, 10}, {68}},
{{-2, 6}, {23}},
{{-3, 6}, {18}},
{{-3, 7}, {15}},
{{-3, 9}, {10}},
{{-3, 11}, {4}},
{{-4, 9}, {12}}
};
indices = Flatten[Position[cells, #] & /@ hints[[All, 1]]];
candidates[[indices]] = hints[[All, 2]];
out = HidatoSolve[cells, candidates];
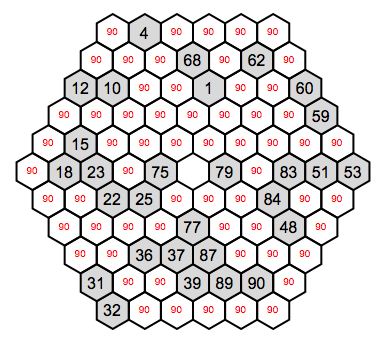
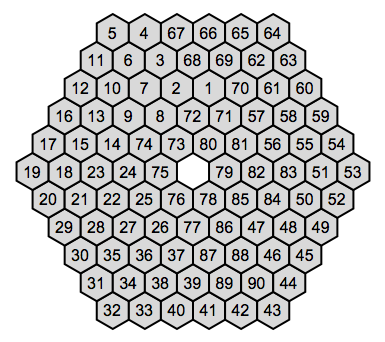
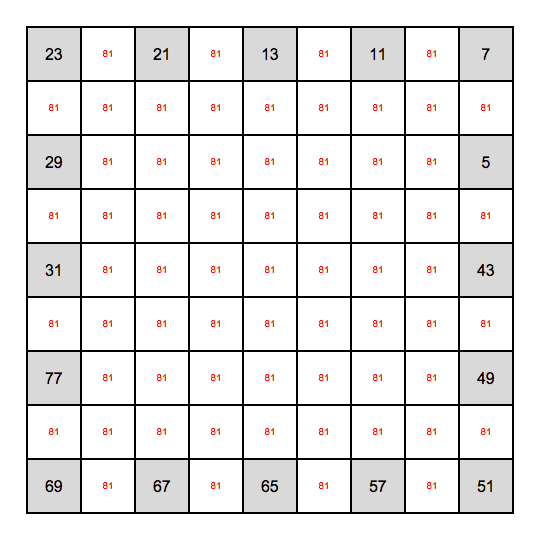
Or with only Horizontal and Vertical connectivity (note that here the end-points are not given!):
$HidatoMode = "Numbrix";
cells = Tuples[Range[9], 2];
candidates = ConstantArray[Range@Length[cells], Length[cells]];
hints = {
{{1, 1}, {69}},
{{3, 1}, {67}},
{{5, 1}, {65}},
{{7, 1}, {57}},
{{9, 1}, {51}},
{{1, 3}, {77}},
{{1, 5}, {31}},
{{1, 7}, {29}},
{{1, 9}, {23}},
{{3, 9}, {21}},
{{5, 9}, {13}},
{{7, 9}, {11}},
{{9, 9}, {7}},
{{9, 7}, {5}},
{{9, 5}, {43}},
{{9, 3}, {49}}
};
indices = Flatten[Position[cells, #] & /@ hints[[All, 1]]];
candidates[[indices]] = hints[[All, 2]];
out = HidatoSolve[cells, candidates];
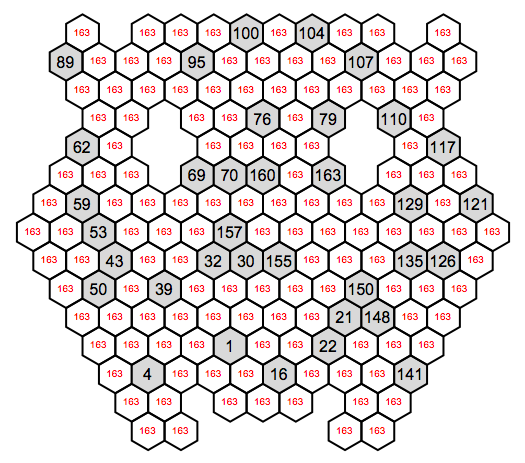
Lastly one of the toughest puzzles I could find, it takes the brute-force solver roughly 20 minutes to solve (after the logic eliminates a lot of candidates):
$HidatoMode="Hex";
cells=Join@@{
{#,1}&/@{1,2,7,8},
{#,2}&/@Join[Range[0,1],Range[3,5],Range[7,8]],
{#,3}&/@Range[-1,8],
{#,4}&/@Range[-2,8],
{#,5}&/@Range[-3,8],
{#,6}&/@Range[-4,8],
{#,7}&/@Range[-5,8],
{#,8}&/@Range[-6,8],
{#,9}&/@Range[-6,7],
{#,10}&/@Join[Range[-6,-4],Range[-2,2],Range[4,6]],
{#,11}&/@Join[Range[-6,-5],Range[-2,1],Range[4,5]],
{#,12}&/@Join[Range[-6,-5],Range[-3,1],Range[3,4]],
{#,13}&/@Range[-7,4],
{#,14}&/@Range[-8,4],
{#,15}&/@Join[{-8},Range[-6,1],{3}]
};
candidates=ConstantArray[Range@Length[cells],Length[cells]];
hints={
{{0,3},{4}},
{{0,7},{32}},
{{0,8},{157}},
{{0,10},{160}},
{{1,7},{30}},
{{1,12},{79}},
{{1,14},{107}},
{{2,4},{1}},
{{2,7},{155}},
{{2,10},{163}},
{{3,12},{110}},
{{4,3},{16}},
{{5,4},{22}},
{{5,5},{21}},
{{5,6},{150}},
{{5,9},{129}},
{{5,11},{117}},
{{6,5},{148}},
{{6,7},{135}},
{{7,7},{126}},
{{7,9},{121}},
{{8,3},{141}},
{{-1,6},{39}},
{{-1,10},{70}},
{{-1,12},{76}},
{{-1,15},{104}},
{{-2,10},{69}},
{{-3,6},{50}},
{{-3,7},{43}},
{{-3,15},{100}},
{{-4,8},{53}},
{{-4,14},{95}},
{{-5,9},{59}},
{{-6,11},{62}},
{{-8,14},{89}}
};
indices=Flatten[Position[cells,#]&/@hints[[All,1]]];
candidates[[indices]]=hints[[All,2]];
out=HidatoSolve[cells,candidates];
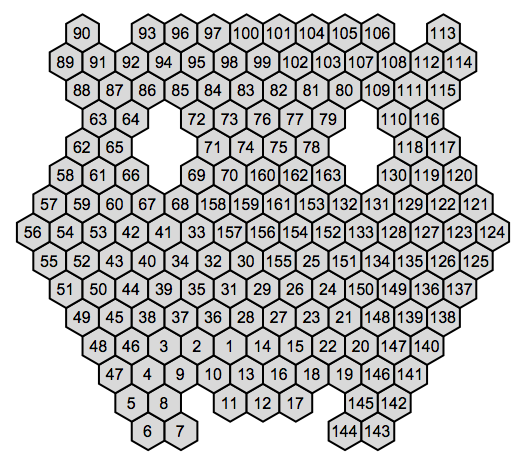
Happy puzzle solving!