list = RandomReal[{-10, 10}, 1000000];

List of codes

ta = Table[taList = {
     (*  1 *)(Total[Abs[list]] + Total[list])/2 // AbsoluteTiming,
     (*  2 *) Total@Ramp@list // AbsoluteTiming,
     (*  3 *) Total@Clip[list, {0, \[Infinity]}] // AbsoluteTiming,
     (*  4 *) Plus @@ Ramp@list // AbsoluteTiming,
     (*  5 *) Plus @@ Clip[list, {0, \[Infinity]}] // AbsoluteTiming,
     (*  6 *) Total@Select[list, Positive] // AbsoluteTiming,
     (*  7 *) Total@Cases[list, _?Positive] // AbsoluteTiming,
     (*  8 *) Plus @@ Cases[list, _?Positive] // AbsoluteTiming,
     (*  9 *) Total@Cases[list, x_ /; x > 0] // AbsoluteTiming,
     (* 10 *) Plus @@ Cases[list, x_ /; x > 0] // AbsoluteTiming,
     (* 11 *) Plus @@ Select[list, # > 0 &] // AbsoluteTiming,
     (* 12 *) Total[list /. b_?Negative -> 0] // AbsoluteTiming,
     (* 13 *) Total[list /. x_ /; x < 0 -> 0] // AbsoluteTiming,
     (* 14 *) Total@Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
     (* 15 *) Plus @@ Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
     (* 16 *)(s = 0; l = Length[list]; 
       Do[If[list[[i]] > 0, s += list[[i]], s], {i, l}]; s) // 
      AbsoluteTiming,
     (* 17 *)(s = 0; l = Length[list]; 
       Table[If[list[[i]] > 0, s += list[[i]], s], {i, l}][[l]]) // 
      AbsoluteTiming,
     (* 18 *)(pcf = Function[x, Piecewise[{{x, x > 0}}, 0], Listable];
        Total[pcf[list]]) // AbsoluteTiming,
     (* 19 *)(s = 0; l = Length[list]; 
       For[i = 0, i <= l, i++, If[list[[i]] > 0, s += list[[i]], s]]; 
       s) // AbsoluteTiming,
     (* 20 *)(s = 0; i = 1; l = Length[list]; 
       While[i <= l, If[list[[i]] > 0, s += list[[i]], s]; i++]; s) //
       AbsoluteTiming
     };
   BarChart[taList[[All, 1]], PlotRange -> {{-.01, 20.5}, {0, 4}}]
   , {48}];

Test Results for a list with 1mln elements

List generation:

list = RandomReal[{-10, 10}, 1000000];

Animation includes the results of 48 tests made both with AbsoluteTiming and RepeatedTiming. The first BarChart is for AbsoluteTiming.

Numerically, we can conclude that the best code is the newest:

Comparing results

In[102]:= absTiming = taList[[All, 1]]

Out[102]= {0.00687931, 0.00704303, 0.015065, 0.359983, 0.321751, 0.683816, 0.779643, \
0.887773, 1.03672, 1.0153, 1.14582, 1.31585, 1.45897, 1.83022, 1.79794, \
2.67337, 2.94904, 3.10739, 3.46186, 3.73936}

In[103]:= absTiming/absTiming[[1]]

Out[103]= {1., 1.0238, 2.1899, 52.3284, 46.7708, 99.4018, 113.332, 129.05, 150.701, \
147.587, 166.561, 191.277, 212.081, 266.048, 261.355, 388.611, 428.682, \
451.701, 503.228, 543.567}

In[108]:= repTiming = trList[[All, 1]]

Out[108]= {0.00618, 0.00703, 0.0147, 0.27, 0.271, 0.638, 0.7696, 0.775, 0.9548, 0.9669, \
1.09, 1.20, 1.368, 1.73, 1.75, 2.60, 2.86, 3.06, 3.5, 3.74}

In[109]:= repTiming/repTiming[[1]]

Out[109]= {1.00, 1.14, 2.38, 44., 43.9, 103., 125., 125., 155., 157., 176., 194., 222., \
280., 283., 421., 463., 495., 5.6*10^2, 6.1*10^2}

Test Results for a list with 20 elements

List generation:

list = RandomReal[{-10, 10}, 20];

Animation includes the results of 60 tests made both with AbsoluteTiming and RepeatedTiming. The first BarChart is for AbsoluteTiming.

Comparing results

In[95]:= abs20Timing = taList20[[All, 1]]

Out[95]= {0.0000166167, 
 4.39853*10^-6, 0.0000151505, 0.0000131956, 0.0000146618, 0.0000244363, \
0.0000268799, 0.0000219927, 0.0000298123, 0.0000254138, 0.0000268799, \
0.0000508275, 0.0000478952, 0.0000444741, 0.0000390981, 0.0000669555, \
0.0000645118, 0.0000772187, 0.0000825947, 0.0000796623}

In[96]:= abs20Timing/abs20Timing[[1]]

Out[96]= {1., 0.264706, 0.911765, 0.794118, 0.882353, 1.47059, 1.61765, 1.32353, \
1.79412, 1.52941, 1.61765, 3.05882, 2.88235, 2.67647, 2.35294, 4.02941, \
3.88235, 4.64706, 4.97059, 4.79412}

In[97]:= rep20Timing = trList20[[All, 1]]

Out[97]= {4.761*10^-6, 2.2*10^-6, 5.53*10^-6, 
 7.6*10^-6, 0.000011419, 0.0000173, 0.000026, 0.00002, 0.000030, 0.000026, \
0.000028, 0.000044, 0.000048, 0.000047, 0.0000413, 0.000073, 0.000069, 0.003, \
0.0001, 0.0000795}

In[98]:= rep20Timing/rep20Timing[[1]]

Out[98]= {1.000, 0.45, 1.16, 1.6, 2.398, 3.62, 5.5, 5., 6.3, 5.5, 5.9, 9.2, 10., 
 1.*10^1, 8.67, 15., 14., 7.*10^2, 2.*10^1, 16.7}

For the short list the code with Total[] and Ramp[] functions is the fastest.

Dear Douglas, Thank you for an impressive code, both very clever and simple. It’s amazing to discover once again that nice things may be done on the basis of very simple and known functions, like these Total[] and Abs[].

Your code together with the above codes are as a challenge for the new fastest code proposal. It will be very amazing if such code or codes will be find.

I am doing now the new tests which include your code too. I will display the results as soon as possible .

Smart! Very nice find! Though compromises readability...

After the release of Mma 11, I introduced, according with Sander suggestion, two new codes with the function Ramp[].

The codes are sorted to emphasize their efficiency.

At the moment, there are 19 codes.

List with 1 mln random generated real elements

First, I have done tests on a list with 1 mln numeric elements

list = RandomReal[{-10, 10}, 1000000];

and AbsoluteTiming 48 repetitions:

ta = Table[tList = {
     (*  1 *) Total@Ramp@list // AbsoluteTiming,
     (*  2 *) Total@Clip[list, {0, \[Infinity]}] // AbsoluteTiming,
     (*  3 *) Plus @@ Ramp@list // AbsoluteTiming,
     (*  4 *) Plus @@ Clip[list, {0, \[Infinity]}] // AbsoluteTiming,
     (*  5 *) Total@Select[list, Positive] // AbsoluteTiming,
     (*  6 *) Total@Cases[list, _?Positive] // AbsoluteTiming,
     (*  7 *) Plus @@ Cases[list, _?Positive] // AbsoluteTiming,
     (*  8 *) Total@Cases[list, x_ /; x > 0] // AbsoluteTiming,
     (*  9 *) Plus @@ Cases[list, x_ /; x > 0] // AbsoluteTiming,
     (* 10 *) Plus @@ Select[list, # > 0 &] // AbsoluteTiming,
     (* 11 *) Total[list /. b_?Negative -> 0] // AbsoluteTiming,
     (* 12 *) Total[list /. x_ /; x < 0 -> 0] // AbsoluteTiming,
     (* 13 *) Total@Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
     (* 14 *) Plus @@ Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
     (* 15 *)(s = 0; l = Length[list]; 
       Do[If[list[[i]] > 0, s += list[[i]], s], {i, l}]; s) // 
      AbsoluteTiming,
     (* 16 *)(s = 0; l = Length[list]; 
       Table[If[list[[i]] > 0, s += list[[i]], s], {i, l}][[l]]) // 
      AbsoluteTiming,
     (* 17 *)(pcf = Function[x, Piecewise[{{x, x > 0}}, 0], Listable];
        Total[pcf[list]]) // AbsoluteTiming,
     (* 18 *)(s = 0; l = Length[list]; 
       For[i = 0, i <= l, i++, If[list[[i]] > 0, s += list[[i]], s]]; 
       s) // AbsoluteTiming,
     (* 19 *)(s = 0; i = 1; l = Length[list]; 
       While[i <= l, If[list[[i]] > 0, s += list[[i]], s]; i++]; s) //
       AbsoluteTiming
     };
   BarChart[tList[[All, 1]], PlotRange -> {{-.01, 19.5}, {0, 4}}]
   , {48}];

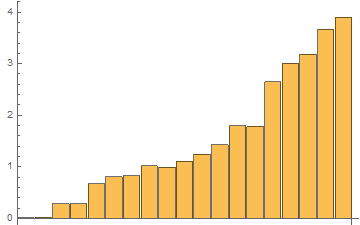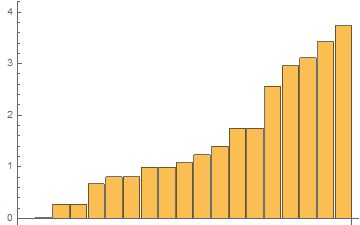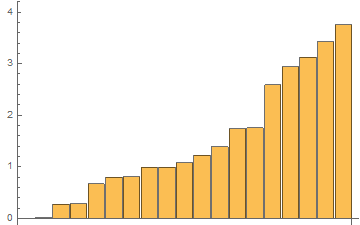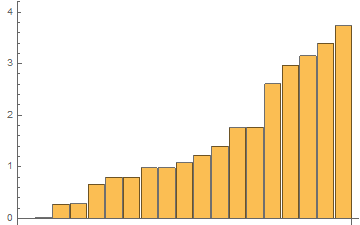
Time results for the last 48th test:

In[1]:= AbsTiming = tList[[All, 1]]

Out[1]= {0.00773412, 0.0147376, 0.273374, 0.285654, 0.659804, \
0.799176, 0.794375, 0.980972, 0.982004, 1.07851, 1.22457, 1.39598, \
1.75444, 1.76957, 2.60787, 2.97176, 3.15208, 3.39943, 3.73759}

In[2]:= AbsTiming/AbsTiming[[1]]

Out[2]= {1., 1.90553, 35.3465, 36.9342, 85.3108, 103.331, 102.711, \
126.837, 126.97, 139.448, 158.333, 180.496, 226.844, 228.8, 337.19, \
384.241, 407.556, 439.537, 483.26}

For the same list with 1 mln elements, the results of 48 tests with RepeatedTiming in one GIF

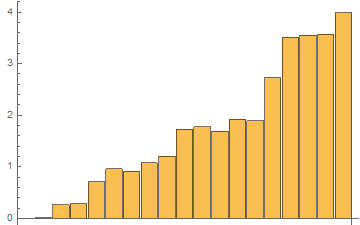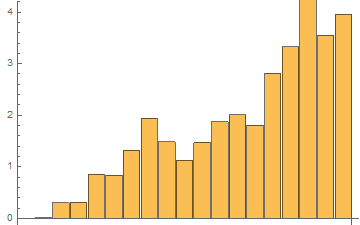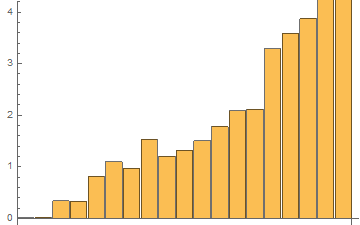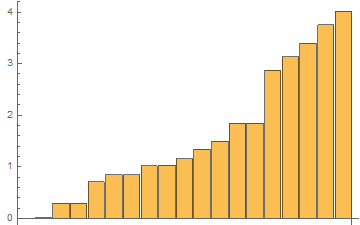
The time results of the last 48th test:

In[3]:= RepTiming = tList[[All, 1]]

Out[3]= {0.0076, 0.015, 0.291, 0.294, 0.708, 0.8480, 0.843, 1.02, \
1.04, 1.2, 1.3, 1.5, 1.84, 1.85, 2.87, 3.13, 3.39, 3.7516, 4.01}

In[4]:= RepTiming/RepTiming[[1]]

Out[4]= {1.0, 2.0, 38., 39., 9.*10^1, 1.1*10^2, 1.1*10^2, 1.3*10^2, 
 1.4*10^2, 1.5*10^2, 1.8*10^2, 2.0*10^2, 2.4*10^2, 2.4*10^2, 3.8*10^2,
  4.1*10^2, 4.5*10^2, 4.9*10^2, 5.3*10^2}

Remark, the first code is 2 times faster than the second code and 530 times faster than the 19th code.

Short list with 20 random generated real elements

Third, I have done tests for a short list with 20 elements and with 120 repetitions with AbsoluteTiming[]

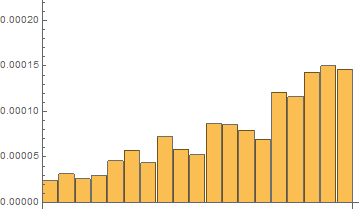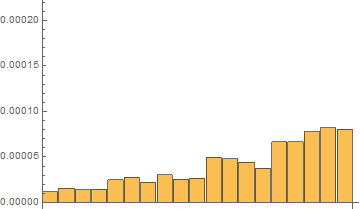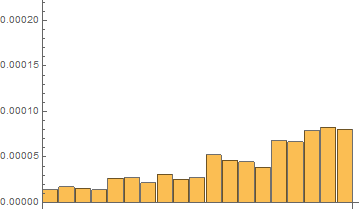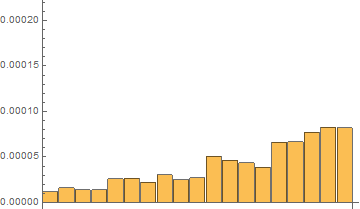
Time results for the last 120th test:

In[5]:= absTiming = tList[[All, 1]]

Out[5]= {0.0000112407, 0.0000156393, 0.0000136844, 0.0000141731, \
0.0000244364, 0.0000263913, 0.0000205266, 0.0000293237, 0.0000239477, \
0.0000259026, 0.0000498502, 0.0000474066, 0.000044963, 0.0000390982, \
0.0000606022, 0.000061091, 0.0000752641, 0.000077219, 0.0000767303}

In[6]:= absTiming/absTiming[[1]]

Out[6]= {1., 1.3913, 1.21739, 1.26087, 2.17391, 2.34783, 1.82609, \
2.6087, 2.13043, 2.30435, 4.43478, 4.21739, 4., 3.47826, 5.3913, \
5.43478, 6.69565, 6.86957, 6.82609}

Fourth, I have done tests with on the same short list with 20 elements with 120 repetitions with RepeatedTiming

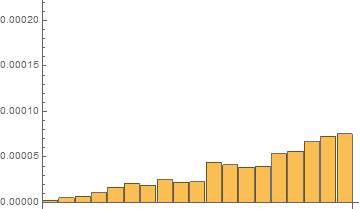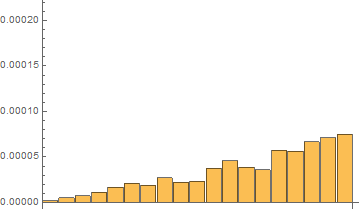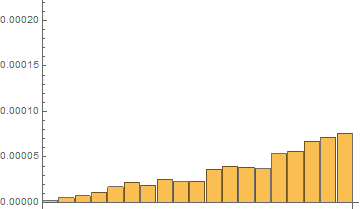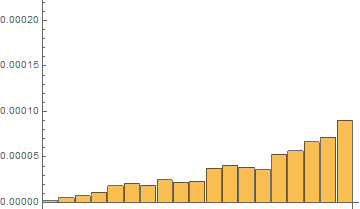
Time results for the last 120th test:

In[7]:= repTiming = tList[[All, 1]]

Out[7]= {2.016*10^-6, 5.33*10^-6, 
 7.16*10^-6, 0.0000110, 0.000019, 0.00002111, 0.0000189, 0.0000249, \
0.00002229, 0.0000230, 0.0000373, 0.0000408, 0.0000387, 0.0000360, \
0.0000532, 0.0000568, 0.0000664, 0.0000718, 0.00009}

In[8]:= repTiming/repTiming[[1]]

Out[8]= {1.000, 2.64, 3.55, 5.48, 9.2, 10.47, 9.4, 12.3, 11.06, \
11.4, 18.5, 20.2, 19.2, 17.8, 26.4, 28.2, 32.9, 35.6, 4.*10^1}

Conclusions

The function Ramp[] together with Total[] is more faster than all the rest of codes as for large lists as for short lists.

These results may serve as a good bases to construct efficient summations in other situations and cases.

These codes are good to use in classrooms as examples of good/efficient and bad/non-efficient programming.

Thank you all for your contributions!

Sorry 'bout that; I've edited the post. I seem to have pasted the wrong snippet.

Bingo?

I found that for small lists the code Total[Clip[list, {0, [Infinity]}]] is not more the fastest. The fastest is a new piece of code

Plus @@ Clip[list, {0, \[Infinity]}]

but only for lists with small dimensions ( = 20). I have done experiments with the following pieces of code

In[428]:= tList = {
  (* 1*) Total[Clip[list, {0, \[Infinity]}]] // AbsoluteTiming,
  (* 2*) Plus @@ Clip[list, {0, \[Infinity]}] // AbsoluteTiming,
  (* 3*) Total[Select[list, Positive]] // AbsoluteTiming,
  (* 4*) Total[Cases[list, x_ /; x > 0]] // AbsoluteTiming,
  (* 5*) Plus @@ Cases[list, x_ /; x > 0] // AbsoluteTiming,
  (* 6*) Plus @@ Select[list, # > 0 &] // AbsoluteTiming,
  (* 7*) Total[list /. x_ /; x < 0 -> 0] // AbsoluteTiming,
  (* 8*) Total@Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
  (* 9*) Plus @@ Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
  (*10*)(s = 0; l = Length[list]; 
    Do[If[list[[i]] > 0, s += list[[i]], s], {i, l}]; s) // 
   AbsoluteTiming,
  (*11*)(s = 0; l = Length[list]; 
    Table[If[list[[i]] > 0, s += list[[i]], s], {i, l}][[l]]) // 
   AbsoluteTiming,
  (*12*)(pcf = Function[x, Piecewise[{{x, x > 0}}, 0], Listable]; 
    Total[pcf[list]]) // AbsoluteTiming,
  (*13*)(s = 0; l = Length[list]; 
    For[i = 0, i <= l, i++, If[list[[i]] > 0, s += list[[i]], s]]; 
    s) // AbsoluteTiming,
  (*14*)(s = 0; i = 1; l = Length[list]; 
    While[i <= l, If[list[[i]] > 0, s += list[[i]], s]; i++]; s) // 
   AbsoluteTiming
  }

Out[428]= {{0.0000371432, 64.4051}, {0.0000244363, 
  64.4051}, {0.0000288349, 64.4051}, {0.0000483839, 
  64.4051}, {0.0000317672, 64.4051}, {0.0000288349, 
  64.4051}, {0.0000562036, 64.4051}, {0.0000498501, 
  64.4051}, {0.0000381207, 64.4051}, {0.0000659781, 
  64.4051}, {0.0000596246, 64.4051}, {0.0000850384, 
  64.4051}, {0.0000762413, 64.4051}, {0.0000772188, 64.4051}}

I observed that if the experiments are repeated, the time results are not the same. You can view this fact in the following animation, which includes 120 repetitions of the same summations on the same list.

A question appears: why the times are different if the code and the list remain unchanged?

I have done the same experiment on the list with 1 mln elements, but providing repetitions only 32 times. The results may be seen in the following GIF

For the large lists, the time behavior of the pieces of code are more stable.

Nevertheless, one more question appears: what is the worst correct piece of code?

May be the following code a pretender to such denomination?

Total[list //. {a___, b_, c___} /; b < 0 -> {a, 0, 
     c}] // AbsoluteTiming

For small lists it works perfect! But for lists with length more than 1000 it requires very long time.

Repeatedly matching the entire list is indeed very likely to be slow, so why do that here? You could do Total[list /. b_?Negative -> 0] if you wish to take the replacement route.

At the moment, there are 8 pieces of code. They are sorted from the fastest to the slowest:

In[47]:= list = RandomReal[{-10, 10}, 1000000];

In[48]:= tList = {
  (*1*) Total[Clip[list, {0, \[Infinity]}]] // AbsoluteTiming,
  (*2*) Total[Select[list, Positive]] // AbsoluteTiming,
  (*3*) Total[Cases[list, x_ /; x > 0]] // AbsoluteTiming,
  (*4*) Plus @@ Select[list, # > 0 &] // AbsoluteTiming,
  (*5*) Total[list /. x_ /; x < 0 -> 0] // AbsoluteTiming,
  (*6*) Total@Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
  (*7*) Plus @@ Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
  (*8*) (pcf = Function[x, Piecewise[{{x, x > 0}}, 0], Listable]; 
    Total[pcf[list]]) // AbsoluteTiming
  }

Out[48]= {{0.0181547, 2.50798*10^6}, {0.656519, 
  2.50798*10^6}, {0.988164, 2.50798*10^6}, {1.0865, 
  2.50798*10^6}, {1.41506, 2.50798*10^6}, {1.77652, 
  2.50798*10^6}, {1.77717, 2.50798*10^6}, {3.21233, 2.50798*10^6}}

The function Total[] is the key to the fast codes. Total[] together with Clip[] form the fastest code:

Total[ Clip[list, {0, $\infty$}] ]

It is 36 times faster than the second code, and 177 times faster than the last!

Sure, I can do it, but for our goals it's not so important! It's just for principles and ideas.

Yes! Simple and Clear!

I'd have done it this way: pcf = Function[x, Piecewise[{{x, x > 0}}, 0], Listable]; Total[pcf[tst]]

You are right, I copied the wrong stuff from my test-notebook... But fixed by JM.. thanks

Then how do you know if they're positive? How do you wish them to be dealt with?

That wasn't an answer to my question. :) If you have a list like {1, 2, x, -1, -4}, should x be added to the sum, or removed from the list before summing? Same question for {1, 2, I, -1, -4}.

And what about the second list I gave? Complex numbers like I are neither positive nor negative.

As you asked me, J.M., about the summation, we can imagine an improvement of the function Total[] that will include the criterion according to which the summation is done, i.e.

Total[list, crit, {Subscript[n, 1],Subscript[n, 2]}]

crit means criterion and it may be, e.g., Reals, Complex, Integers, and so on...

Thanks a lot, J.M.

Yes, it is the fastest! It is the lowest bar in the precedent BarChart!

Thanks!

In[6]:= list = RandomReal[{-10, 10}, 1000000];

In[10]:= tList = {
Plus @@ Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
Total@Map[If[# < 0, 0, #] &, list] // AbsoluteTiming,
Total[list /. x_ /; x < 0 -> 0] // AbsoluteTiming,
Plus @@ Select[list, # > 0 &] // AbsoluteTiming,
Total[Clip[list, {0, \[Infinity]}]] // AbsoluteTiming
}

Out[10]= {{1.76125, 2.49895*10^6}, {1.78087, 2.49895*10^6}, {1.42525,  2.49895*10^6},
{1.07893, 2.49895*10^6}, {0.0146056, 2.49895*10^6}}

In[11]:= BarChart@tList[[All, 1]]

Unbelievable fast!

Fantastic! Thanks a lot! You are magician!

It's very impressive for me!

To be more specific:

Version 11 will feature Ramp that slices the timings of Clip in half:

http://reference.wolfram.com/language/ref/Ramp.html