Introduction to the Problem
While a gate-based quantum computer has yet to be implemented at the level of more than a handful of qubits, and some worry that the decoherence problem will remain an obstacle to real-world use of these machines; the field of theoretical quantum computing has its own virtue apart from these problems of construction and implementation. The theory of quantum computation and quantum algorithms have been used as powerful tools to tackle long-standing problems in classical computation such as proving the security of certain encryption schemes and refining complexity classifications for some approaches to the Traveling Salesman problem. Moreover, learning how to apply quantum effects like superposition, interference, and entanglement in a useful, computational, manner can help students gain a better understanding of how the quantum world really works. These educational and research advantages of quantum computing, along with the ever-present goal of designing new quantum algorithms that can provide us with speedups over their classical counterparts, furnish ample reason to make the field as accessible as possible. The goal of this project was to do just that by using the Wolfram language to design functionality that allows for researchers and students alike to engage with quantum computing in a meaningful way.
Getting it Done
This project involved the design and development of a suite of functions that allows for the simulation of quantum computing algorithms. The overarching goal was a framework that allows for easy implementation of quantum circuits, with minimal work done by the user. The specific design challenges were to have a tool simple enough to be used as an educational aide and powerful enough for researchers. To this end circuits can be built iteratively, allowing students, and those new to quantum computing, to build a working knowledge of the field as they increase the complexity of the algorithms. The system has a universal set of gates allowing it to carry out any operation possible for a quantum computer (up to limits on the number of qubits due to the size of the register).
Short note on this: I have not rigorously tested the system yet, but unless you want to wait several hours for your computation to complete, I suggest not attempting computations with more than ~20 qubits. To classically simulate an N-qubit register, requires a state vector of length 2N. Interestingly, it is this insight into the computational difficulty of simulating a quantum state that led Feynman to realize the power that quantum computing could have.
The project has functionality for the following gates: Hadamard, X, Y, Z, Rotation (any angle, about any axis), C-NOT, C-anything, SWAP, and QFT. It takes input in standard quantum circuit notation, and can output circuit diagrams, and the corresponding unitary transformation matrix as well as return the probabilities for results of measurements on a given qubit. Moreover, there is built in functionality for easy circuit addition, allowing one to stitch together large circuits from smaller ones, a boon for comprehension and testing.
A Simple Example
We initialize some random circuit by specifying it's corresponding circuit notation. For sake of brevity, we start with a medium-sized circuit that is already formed, and perform operations on it, but one can easily build a circuit up qubit-by-qubit and gate-by-gate with the applyQ and circuitQ functions. Below we name some variable quantumCircuit using the function circuitQ to which we pass some circuit notation. This notation is just a matrix representing the quantum logic circuit, with the gates and qubits arranged schematically.
quantumCircuit= circuitQ[{{"H", "R[1,Pi/2]", "N", "SWAP1"}, {"H", 1, "C",
"SWAP2"}, {"X", 1, "C", 1}}];
circuitQ outputs the circuit diagram corresponding to the notation given:
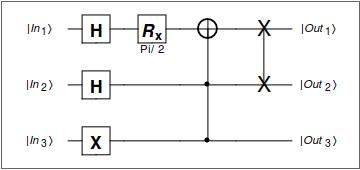
But, say I wish to alter the circuit. We can add in as many layers of gates or extra qubits as we wish, without having to deal with the pesky notation matrix. Here I add a Hadamard gate to the second qubit after the SWAP using the function applyQ:
applyQ[quantumCircuit, "H", 2]
the output of which is:
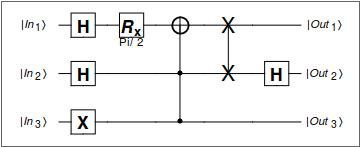
One can also use Append, Join,Nest and a variety of other Wolfram language functions to build up highly complex circuits. However, the circuitQ function is overloaded, and one can also perform computations with it. We will now build the actual unitary transformation matrix that corresponds to the circuit diagram:
unitar=matrixBuild@quantumCircuit
which, for our circuit, produces:
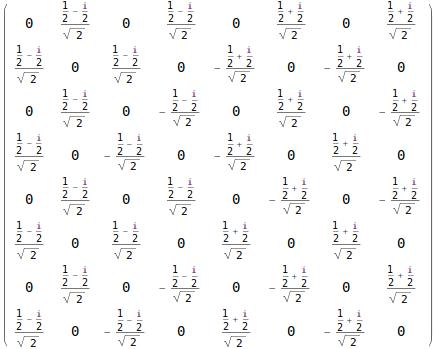 .
.
Now we can easily perform operations with circuit. Let's specify some random 3 qubit initial state (in the computational basis):
initalState = {1, 0, 0, 1, 0, 0, 1, 0} // Normalize
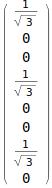
We can pass this initial state to the circuit easily with:
premeasure=unitar.initialState
which gives back the state of the quantum register (in this case our 3 qubits) after they have been operated on by the circuit, but pre-measurement:
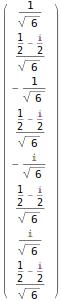
We can now sample our state using the projection function. Here we will calculate the probability of getting state |0> when measuring qubit #3:
projection[2,0,premeasure]
which, for our case, gives back a probability of 2/3.
Wrap Up
This was only a very simple example. Using applyQ and circuitQ one can build and modify highly complex quantum circuits easily. matrixBuild does all the math of calculating the corresponding unitary transformation matrix for you. All that is left is for the user to pass an initial state and see the output. A good learning technique is to start with a very simple circuit and initial state, and slowly build up in complexity, performing measurements at each step, to build an intuition and working knowledge of any given quantum circuit.
An obvious next step for the project would be to add functionality that allows for the easy implementation of a general quantum oracle. I would also like to add more gates to the gate library, including: $\sqrt{SWAP}$, Tofolli, and QFT-1 which were left out due to lack of time and are trivial to implement. These tools would make it significantly easier for researchers to model any given quantum circuit.
Where is the NKS?
Finding quantum algorithms that perform useful tasks faster than their classical counterparts is an open area of research. However, it is often quite difficult to design these algorithms to take advantage of interference, as well as the structure in a given computational problem that may be useful to exploit. As such, there are only a small number of important quantum algorithms that are currently known. Hopefully this tool will allow for NKS-style search experiments for interesting behavior in quantum circuits. Similar searches have been carried out for classical circuits, and the tools I built will make it easy to generate vast sets of random quantum circuits that follow certain rules. What remains is to build useful analytic tools for combing the space.