In this post it is presented a WL procedure to compute the geodetic coordinates of the oceanic pole of inaccessibility, also known as "Nemo point". This is the point in the ocean which is farthest from any land. This post takes some code from this earlier post in this same group.

Fast way to decide if a geodetic location is inland or not

Check whether we are inland or not using GeoElevationData:

In[1]:= Dimensions[
 elevation = 
  Reverse@QuantityMagnitude[
    GeoElevationData["World", GeoZoomLevel -> 5]]]

Out[1]= {4096, 8192}

We create an interpolating function from the data:

In[2]:= elevationF = ListInterpolation[elevation, {{-90, 90}, {-180, 180}}]
Out[2]= InterpolatingFunction[{{-90., 90.}, {-180., 180.}}, <>]

Check using the interpolating function whether a point is inland or not:

In[3]:= inlandQ[{lat_, lon_}] := 
Greater[elevationF[lat, Mod[lon, 360, -180]], 0];

Example:

In[4]:= First[Here]

Out[4]= {40.32, -3.87}

In[5]:= % // inlandQ // AbsoluteTiming

Out[5]= {0.000071, True}

Computation of Nemo point

Computation of a geodesic path from a point at sea to the coast for a given azimuth:

In[6]:= geopath[point_, azimuth_Real, dist_] := 
 Module[{points, ipoints, len},
(* Geodetic coordinates of a set of points contained in a geodesic arc of distance dist, in meters *)
  points = 
   Reverse /@ (GeoGraphics`GeoEvaluate[
       GeoPath[{GeoPosition@point, dist, azimuth}], Automatic, 
       100000] /. Line -> Identity);
(* Check which points of the geodesic arc are inland *)
  ipoints = inlandQ /@ points;
(* Select those points of the geodesic arc which are on the sea *)
  len = Position[ipoints, True][[1, 1]];
  GeoPath[Take[points, len], "TravelPath", 
   VertexColors -> {Green, Red}]
  ]

Shortest distance (in Kilometers) from a point at sea to the coast for a given azimuth:

 In[7]:= coastDistance[{lat_, lon_}][azimuth_Real] := 
 QuantityMagnitude@GeoLength@geopath[{lat, lon}, azimuth, 40000000]

Minimum distance from a point at sea to the coast:

In[8]:= df[{phi_Real, lambda_Real}] := 
 First@NMinimize[{coastDistance[{phi, lambda}][theta], 
    0. <= theta <= 360.}, theta]

We need to have an estimation of the computational time of the previous function for each point:

In[9]:= point = RandomPoint[RegionProduct[Interval[{-90, 90}], Interval[{-180, 180}]]]

Out[9]= {-15.9345, -36.3062}

In[10]:= inlandQ@%

Out[10]= False

In[11]:= df@point // Timing

Out[11]= {16.0386, 300.752}

Based on this estimation we run a first pass on the whole Earth to get an approximate localization of Nemo point:

In[12]:= Flatten[CoordinateBoundsArray[{{-90., 90.}, {-180., 180}}, 60], 1]

Out[12]= {{-90., -180.}, {-90., -120.}, {-90., -60.}, {-90., 0.}, {-90., 
  60.}, {-90., 120.}, {-90., 
  180.}, {-30., -180.}, {-30., -120.}, {-30., -60.}, {-30., 
  0.}, {-30., 60.}, {-30., 120.}, {-30., 
  180.}, {30., -180.}, {30., -120.}, {30., -60.}, {30., 0.}, {30., 
  60.}, {30., 120.}, {30., 
  180.}, {90., -180.}, {90., -120.}, {90., -60.}, {90., 0.}, {90., 
  60.}, {90., 120.}, {90., 180.}}

The following computation takes about eight minutes in a processor of the Intel i7 family:

In[13]:= df /@ % // Timing

Out[13]= {516.948, {0., 0., 0., 0., 0., 0., 0., 802.006, 3308.28, 0., 1604.01, 
  1403.51, 0., 802.006, 2506.27, 401.003, 1503.76, 0., 0., 0., 
  2506.27, 802.005, 802.005, 802.005, 802.005, 802.005, 802.005, 
  802.005}}

In[14]:= Max@Last@%

Out[14]= 3308.28

The previous value corresponds to GeoPosition[{-30,-120}]. Next we use this location as the starting point of FindMaximum to compute the actual geodetic coordinates of Nemo point and its distance to the nearest coast. The computation takes about 38 minutes in a processor of the Intel i7 family:

In[15]:= nemopoint = 
 FindMaximum[
   df[{phi, lambda}], {{phi, -30.}, {lambda,-120.}}, Method -> "PrincipalAxis"] // Timing

Out[15]= {2322.66, {5012.53, {phi -> -29.3559, lambda-> -130.967}}}

In[16]:= nemoposition = 
 GeoPosition[{phi, lambda}] /. Last@Last@nemopoint

Out[16]= GeoPosition[{-29.3559, -130.967}]

We compute the azimuth of the shortest geodesic arc from Nemo point to the coast:

In[17]:= NMinimize[{coastDistance[First@nemoposition][theta], 
  0. <= theta <= 360.}, theta]

Out[17]= {5012.53, {theta -> 179.129}}

In[18]:= nemoazimuth = theta /. Last@%

Out[18]= 179.129

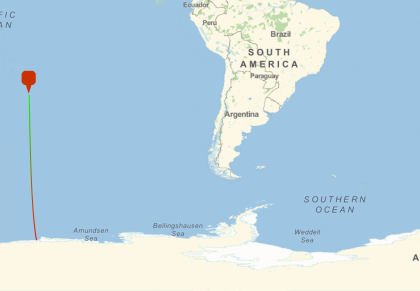
Visualization of the shortest geodesic arc from Nemo point to the coast:

In[19]:= GeoGraphics[{GeoMarker@nemoposition, 
  geopath[First@nemoposition, nemoazimuth, 40000000]}, 
 GeoRange -> {{-90, 0}, {-140, -10}}]

These are the coordinates of the Nemo point as given by independent sources in the Internet:

In[20]:= nemoInternet = 
 GeoPosition[-FromDMS /@ {"48\[Degree]52.6'", "123\[Degree]23.6"}]

Out[20]= GeoPosition[{-48.8767, -123.393}]

The closest land to true Nemo point is not in the elevation data we sampled and this is why we didn't get its exact value. Our result is however exact if continental landmasses are only considered (i.e. the point obtained here is the point in the ocean which is farthest from any continental landmass).