Cellular Automata Classification Problem using Machine Learning.

Cellular Automata, mathematical systems that are governed by simple behavioral rules, are useful in modeling different physical, biological and chemical processes and are also interesting abstract mathematical objects. There are four types of CA distinguished by their pattern: 1. disappearing with time

2. evolves to the fixed size

3. grows infinitely at fixed speed

 4. grows and contracts irregularly

In my project I have tried to test my theory of how reasonable to take such parameters as information entropy and compressibility for classifying 256 elementary CA rules into these classes using Machine Learning.

Introduction. Cellular Automata are very mysterious mathematical systems.Even though they are descibed by very simple rules it is almost imposible to give strict mathematical criteria for distinguishing their class by their evolution. But human mind somehow manages to do that task. I think that one of the main reasons for that is that human brain always takes a bigger picture of the system and works principally other way than machine do. That is why using Machine Learning which imitates human thinking might be very effective method for solving this problem.

Generating Dataset The very first thing that I have done was generating my CA dataset for my research. It was done by using standart built-in Mathametica function for creating Cellular Automaton with certain rule, initial condition number of evolution steps.

ca[r_]:=CellularAutomaton[r,RandomInteger[1,100],200];
cadata = Flatten[Map[Table[ca[#], {10}] &, Range[255]], 1];

For every Rule there are 10 Cellular Automata with 10 random initial conditions that have format of sequences of "1"s and "0"s. Whole dataset includes 2560 CA for all 256 rules which is enough big to feed classifier function.

Entropy

Then I have tried to apply entropy function to every element of my dataset but one problem occured.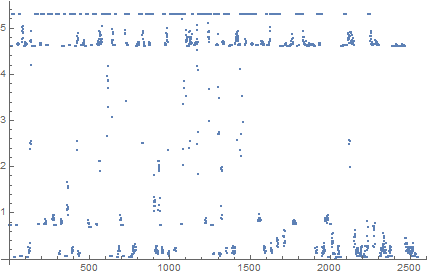

Applying entropy function directly resulted some elements from different classes to have same value of entropy. For example Rule 110 and Rule 30 had exactly same entropy value, but they belong to different classes.

Rule 110

Rule 30

Trying different approach increased precision. Instead of calculating the entropy of whole automaton I have been partitioning it into blocks of {k,k} size and taking the size of the block which has maximum value of entropy forming pairs of two numbers for each automaton {k- size of the of the block that has maximum value of entropy, maximum entropy value itself}.

enTplO[m_]:=
With[{w=Dimensions[m][[2]]},
ListPlot[
Table[
    {k,
    N[Entropy[
        Flatten[
            Partition[m,{k,k}]
        ,1]
    ]]
    },
{k,1,w}],
PlotTheme->"Detailed"
]
]

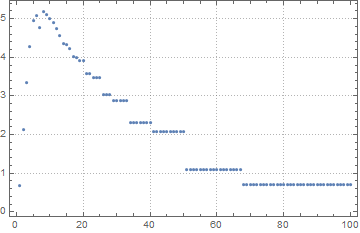
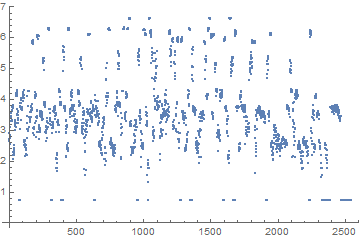
Compressibility

Then I try to give another complexity measure by calculating how much my cellular automata can be compressed.

comp[d_]:=N[ByteCount[Compress[d]]/ByteCount[d]];

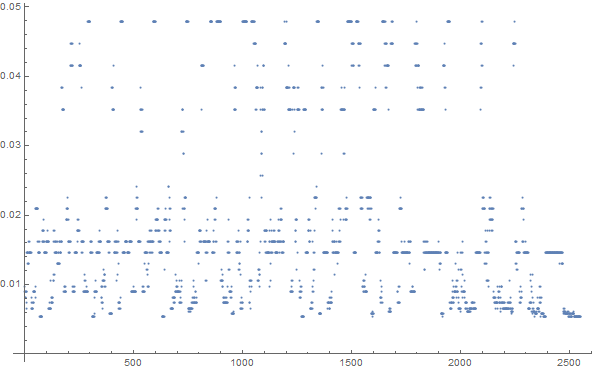
Clustifier Function So now we have 3 parameteres to feed our classifier function {max entropy of CA parts, dimension of that part, compressibility}.

Each of these tuples is a point in 3D space.

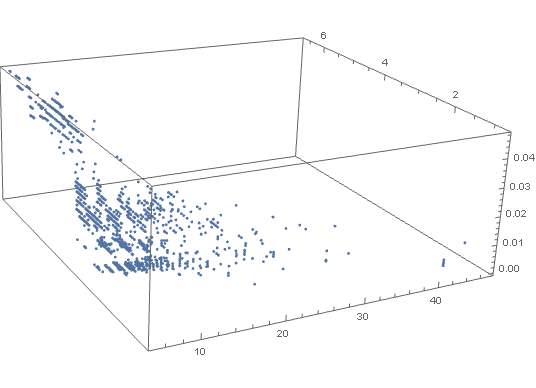
After using Unsupervised Learning the classifier function produced 4 clusters. Result Cluster 1

Cluster 2

Cluster 3

Cluster 4

Conclusion

Although this method isn't very accurate but futher improvemets and adding new macroparameters may give more precise result.

Attachments: