The La Jolla Covering Repository has a collection of covers. For example, my post Smallest Project Space has the C(15,3,2) cover. From numbers to 15, lines of 3 cover all possible subsets of 2, in 35 lines. No subset is reused anywhere within the lines, so this is called a perfect covering. Another well known example is the Golay code C(24,8,5). From numbers to 24, lines of 8 cover all possible subsets of 5, in 759 lines.

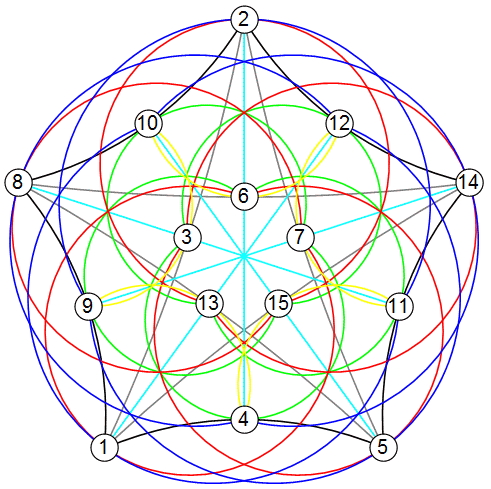
I wondered what the status was for perfect coverings, so I took a look.

C(7,3,2) (Fano plane), C(9,3,2), C(13,3,2), C(15,3,2) (smallest projective space), C(19,3,2), C(21,3,2), C(25,3,2), and more with mod-6 equal to 1 or 3: 27, 31, 33, 37, 39, 43, 45, 49, 51, 55, 57.

C(13,4,2), C(16,4,2), C(25,4,2), C(28,4,2), C(37,4,2), C(40,4,2), and more with mod 12 equal to 1 or 4: 49, 52, 61, 64, 73, 76, 85, 88, 97, 100.

C(21,5,2), C(25,5,2), C(41,5,2), C(45,5,2), and more with mod 20 equal to 1 or 5: 61, 65, 81, 85.

Then things start getting interesting. C(31,6,2), C(66,6,2), C(76,6,2), C(91,6,2), C(96,6,2) are all solved. C(36,6,2), C(46,6,2), C(51,6,2), C(61,6,2), C(81,6,2) are all unsolved. A solution may exist when mod 15 equals 1 or 6.

C(49,7,2) is solved, the rows, columns, and toroidal diagonals of both squares below give the 56 lines needed. C(91,7,2) is also solved. C(43,7,2) and C(85,7,2) are unsolved.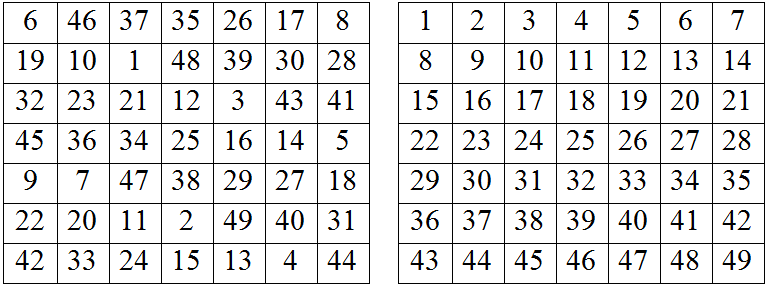

C(57,8,2) and C(64,8,2) are solved. C(73,9,2) and C(81,9,2) are solved.

C(8,4,3), C(10,4,3), C(14,4,3), C(16,4,3), C(20,4,3) are solved, and more where mod 6 equals 1 or 5: 22, 26, 28, 32, 34, 38, 40, 44, 46, 50, 52, 56, 58.

C(17,5,3) and C(26,5,3) are solved. C(22,6,3) is solved, this is known as the M22 graph. C(26,6,3) is solved. C(37,7,3) is unsolved.

C(11,5,4), C(23,5,4), and C(35,5,4) are solved. C(27,6,4) is solved, C(42,6,4) is unsolved. C(23,7,4) is solved, the ternary Golay code.

For small coverings, that's pretty much all that's known. I was surprised at how many cases were unsolved. Also, many of the solutions don't yet have good pictures.