This is a discussion about the findings regarding Hadamard matrices which I researched during my time at the Wolfram High School Summer Camp during the summer of 2016. The motivation behind exploring the many interesting aspects of Hadamard matrices was provided mainly through the functionality of the Wolfram Language. Attached is a Mathematica notebook with all the relevant code used in generating the data and results discussed in this post.

Hadamard Matrices

Hadamard matrices are square matrices which are defined with elements either 1 or -1 such that its rows are orthogonal. It is known that the order of Hadamard matrices can only be 1, 2, or 4n, where n is any positive integer. Another property of Hadamard matrices is that it its inverse is a scalar multiple of itself: multiplying a Hadamard matrix of order n by its transpose yields nI, where I is the n x n identity matrix. Hadamard matrices have applications in error-correcting codes and in statistical parameter estimation. This post will first discuss methods of extending Hadamard matrices to three dimensional cubes, and then discuss how close {1, -1} two dimensional matrices of other orders tend to be to Hadamard matrices.

Sylvester’s Construction

Sylvester’s construction takes a Hadamard matrix of order n and always yields a Hadamard matrix of order 2n. Sylvester’s matrices are a subset of Hadamard matrices formed by repeated application of Sylvester’s construction to the identity matrix of order 1.

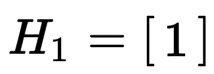
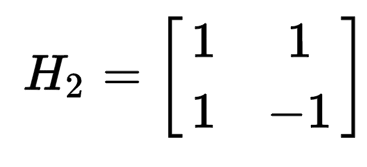
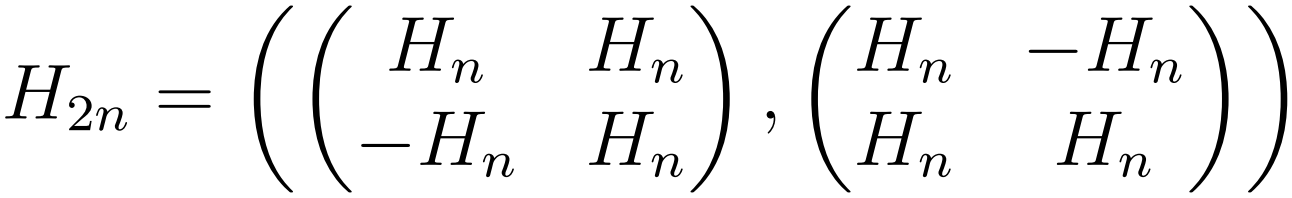
The construction for Sylvester’s matrices is based upon the Hadamard matrix of order 2.

3D Hadamard Cubes

A Hadamard cube is a three dimensional cubic matrix indexed by i, j, and k such that any cross section taken parallel to the i-j plane, the j-k plane, or the k-i plane is a Hadamard matrix.

A class of Hadamard matrices analogous to Sylvester’s matrices can be constructed recursively with a method similar to Sylvester’s construction. The three dimensional matrices were generated by iterating the Kronecker Product over the order 2 Hadamard cube (H2).

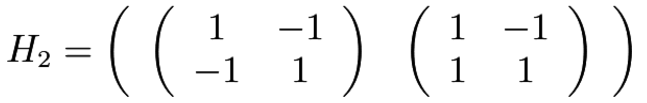
Proof of 3D Construction

I claim that the following formula holds for a special class of three dimensional Hadamard matrices analogous to Sylvester’s matrices:

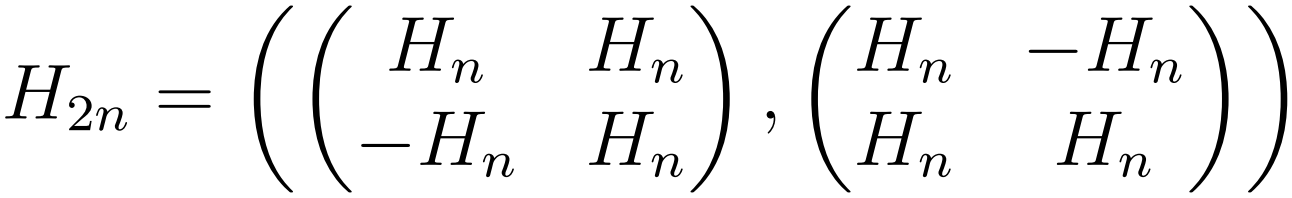
All cross-sections of this cube will cut through exactly 3 Hn’s and 1 -Hn. Transposing the rows or columns of the Hadamard matrix count as a symmetry under the orthogonality condition. Therefore, all cross-sections taken from the H2n cube can be transformed with transpositions to give a Hadamard matrix of the same form as [1]. Below are examples of Hadamard cubes generated with this recursive method. A small blue cube represents a 1, whereas a small red cube represents a -1.

3D Hadamard Cube Examples

Approximate Hadamard Matrices

Returning to the 2 dimensional world, matrices close to Hadamard matrices can be used in instances for which a Hadamard matrix does not exist. The “error” of a matrix defined in this post is calculated by taking the total of the absolute values of the pairwise dot products of its rows.

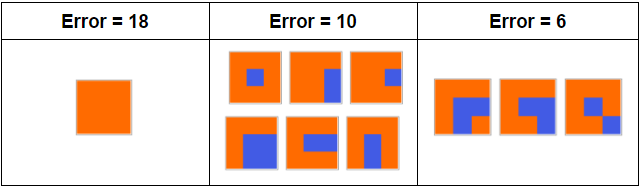
Above, all 3x3 matrices, ignoring symmetries, with their respective error values are shown. An orange grid represents a 1, whereas a blue grid represents a -1. Equivalent cases are omitted.

Hadamard Error Distribution

Observing the distribution of frequency of Hadamard error values for various sizes leads to surprising results. It is unknown what exactly characterizes these distributions, but by analyzing the the distribution calculated at n <= 6 orders, a pattern seems to emerge at n = 6.

Standardized Hadamard Error Distributions

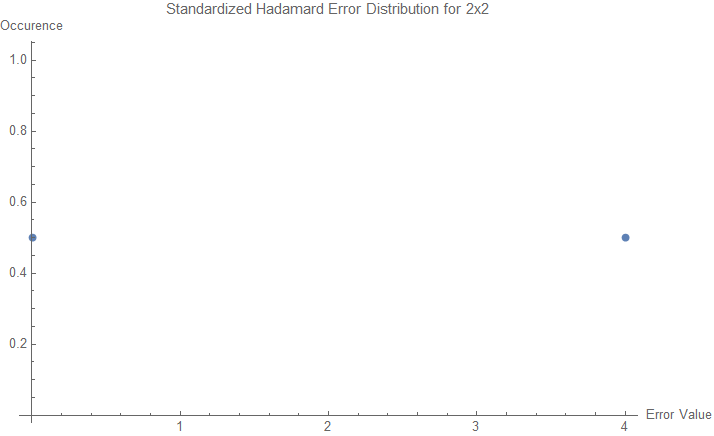
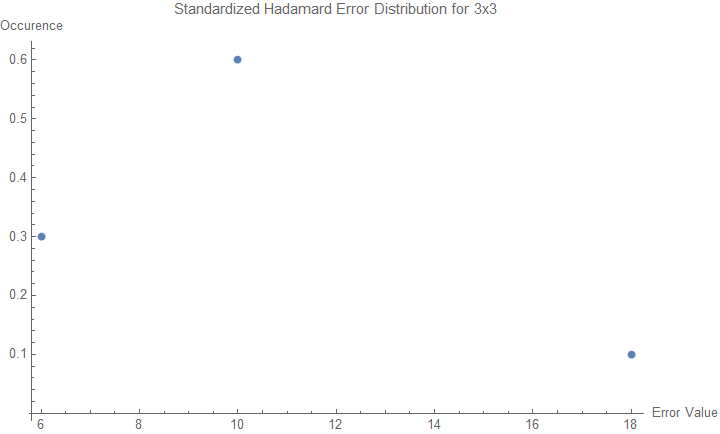
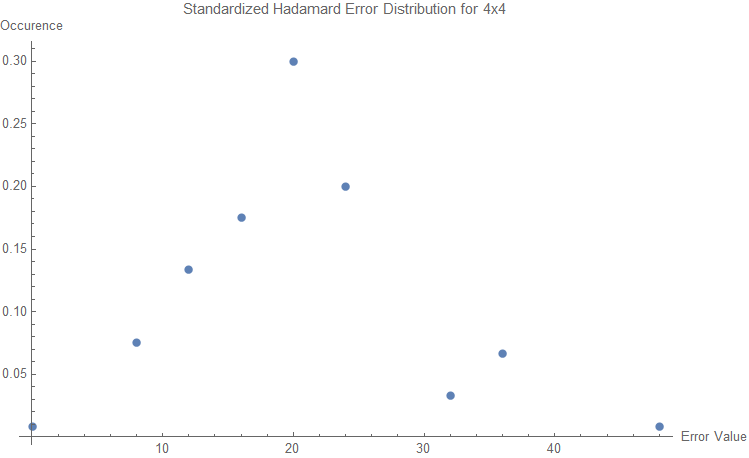
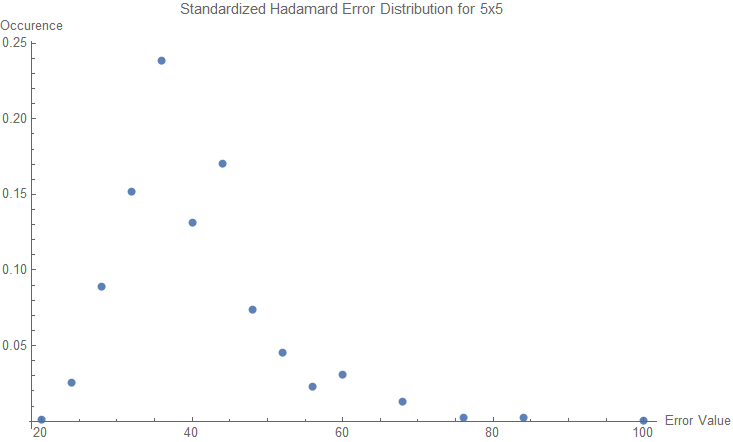
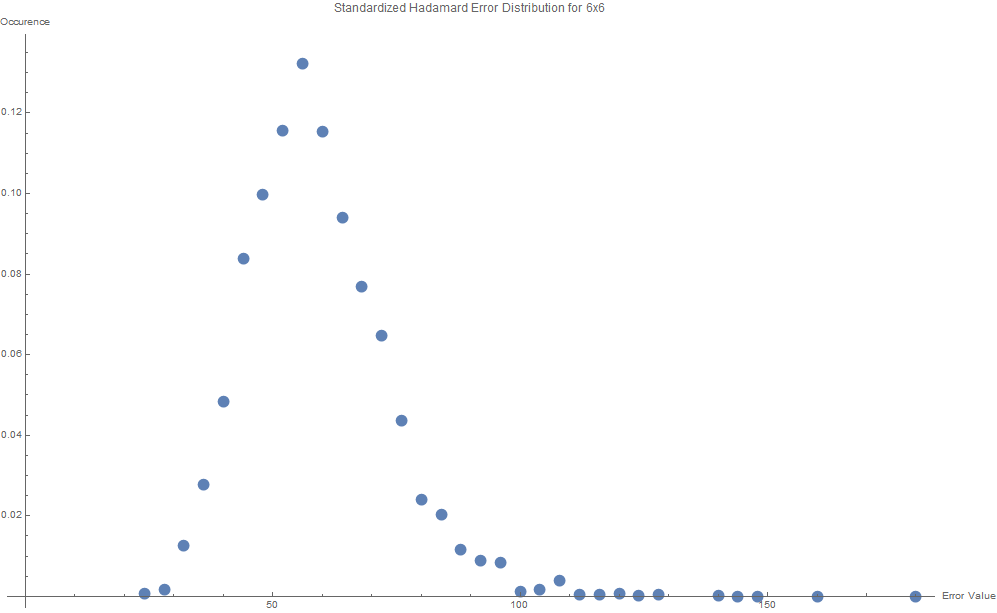
Conclusion

From the topics investigated in this study, further research can be done on the patterns found in the error distribution at higher orders. Since a proven method of generating Hadamard cubes has been shown in this paper, exploring the idea of three dimensional cellular automata could reveal a rule that generates Hadamard cubes similar to the analogous Sylvester constructions.

Attachments: