Group Abstract Group Abstract

Message Boards Message Boards

Seam carving (liquid or content aware rescaling) in Wolfram Language

MODERATOR NOTE: a resource function based on this work is now available:
https://resources.wolframcloud.com/FunctionRepository/resources/ContentAwareImageResize/

  • Update 1: Now forward energy is also implemented.
  • Update 2: Now also extending an image has been implemented.

Seam carving

enter image description here

Hi All,

As you know Wolfram Language can do a lot of image processing, but one thing it can't yet do is so-called liquid rescaling. Liquid rescaling is a way of cropping the image but as opposed to ImageCrop it is content-aware. Meaning it will crop first parts of the image that have less 'information'. I'll show you how we can implement such cropping in Wolfram Language. We start of with importing an image:

img=Import["tower.png"];

enter image description here

I now define a so-called energy function that describes where the image is information-rich:

EnergyFunction[img_Image] := GradientFilter[img, 1, Method -> "ShenCastan"]

We can test this out:

EnergyFunction[img]

giving:

enter image description here

Now the idea is to find vertical 'seams' such that the sum of the values of the energy function along a seam is as low as possible. This seam contains the least of 'energy' or 'information' and we will therefore remove it first. We have to use the following code to do that:

MinFilter1[x_List] := Min /@ Partition[x, 3, 1, {2, 2}, 1.0 10^6] (* same as MinFilter[x,1] but 10x faster *)
MinPosition[x_List] := First[Ordering[x, 1]] (* position of min element *)
Neighbours[n_Integer?Positive, len_Integer?Positive] := Which[n == 1, If[len > 1, {1, 2}, {1}],
  n == len, If[len > 1, {len, len - 1}, {1}],
  True, {n - 1, n, n + 1}
  ]
FindSeam[mat_List?MatrixQ] := 
 Module[{dimx, dimy, seam, neighbours, values, newpos, ii},
  {dimy, dimx} = Dimensions[mat];
  seam = ConstantArray[-1, dimy];
  seam[[-1]] = MinPosition[mat[[-1]]];
  Do[
   neighbours = Neighbours[seam[[ii + 1]], dimx];
   values = mat[[ii, neighbours]];
   newpos = neighbours[[MinPosition[values]]];
   seam[[ii]] = newpos
   ,
   {ii, dimy - 1, 1, -1}
   ];
  seam
  ]
ComputeEnergyField[img_Image] := FoldList[#2 + MinFilter1[#1] &, ImageData[EnergyFunction[img]]]
ComputeEnergyField[mat_List] := ComputeEnergyField[Image[mat]]

we can now test it out:

seam = FindSeam[ComputeEnergyField[img]];
HighlightImage[img, Transpose[{seam, Range[Length[seam]]}]]

seam will be a list of horizontal position of the pixel for each row of pixels. We can use HighlightImage to see the 'seam':

enter image description here

We can remove (carve) that seam from the original image, after which we can repeat this process over and over and crop 1 pixel each time until we have the width that we need (note that we need to recalculate the energy function after every carve). Of course one could do the same with horizontal seams if one wants to crop in the vertical direction. Simply use the same code but rotate the image 90 degrees, remove some seems, and then rotate is 90 degrees back.

To make it more interactive we can calculate all the seems and save these separately, after which we can very easily crop to a desired width:

ClearAll[MinFilter1, MinPosition, Neighbours, FindSeam, EnergyFunction, ComputeEnergyField, Carve, FillNthPosition, CreateSeamcarveImageData, SeamCarve]
MinFilter1[x_List] := Min /@ Partition[x, 3, 1, {2, 2}, 1.0 10^6] (* same as MinFilter[x,1] but 10x faster *)
MinPosition[x_List] := First[Ordering[x, 1]] (* position of min element *)
Neighbours[n_Integer?Positive, len_Integer?Positive] := Which[n == 1, If[len > 1, {1, 2}, {1}],
  n == len, If[len > 1, {len, len - 1}, {1}],
  True, {n - 1, n, n + 1}
  ]
FindSeam[mat_List?MatrixQ] := 
 Module[{dimx, dimy, seam, neighbours, values, newpos, ii},
  {dimy, dimx} = Dimensions[mat];
  seam = ConstantArray[-1, dimy];
  seam[[-1]] = MinPosition[mat[[-1]]];
  Do[
   neighbours = Neighbours[seam[[ii + 1]], dimx];
   values = mat[[ii, neighbours]];
   newpos = neighbours[[MinPosition[values]]];
   seam[[ii]] = newpos
   ,
   {ii, dimy - 1, 1, -1}
   ];
  seam
  ]
EnergyFunction[img_Image] := GradientFilter[img, 1, Method -> "ShenCastan"]
ComputeEnergyField[img_Image] := FoldList[#2 + MinFilter1[#1] &, ImageData[EnergyFunction[img]]]
ComputeEnergyField[mat_List] := ComputeEnergyField[Image[mat]]
Carve[mat_List?ArrayQ, seam_List] := MapThread[Delete, {mat, seam}, 1]
FillNthPosition[x_List, n_Integer?Positive, fill_, empty_: 0] := 
 Block[{pos, out},
  out = x;
  pos = Position[out, empty, {1}, n, Heads -> False];
  out[[pos[[n]]]] = fill;
  out
  ]
CreateSeamcarveImageData[img_Image] := Block[{imagedata, dims, dimx, dimy, carveinfo, seam, energyinfo},
  imagedata = ImageData[img];
  dims = {dimy, dimx} = Dimensions[imagedata, 2];
  carveinfo = ConstantArray[0, dims];
  PrintTemporary[Dynamic[Row[{"Calculating: ", i, "/", dimx}]]];
  Do[
   energyinfo = ComputeEnergyField[imagedata];
   seam = FindSeam[energyinfo];
   carveinfo = 
    MapThread[FillNthPosition[#1, #2, i, 0] &, {carveinfo, seam}];
   imagedata = Carve[imagedata, seam];
   ,
   {i, dimx}
   ];
  {img, carveinfo}
  ]
SeamCarve[{img_Image, carveinfo_List}, n_Integer?NonNegative] := Block[{imgdata, pick, sel, m},
  imgdata = ImageData[img];
  If[Dimensions[imgdata, 2] == Dimensions[carveinfo],
   m = Clip[n, {0, Length[carveinfo[[1]]] - 1}];
   sel = UnitStep[m - carveinfo];
   Image[Pick[ImageData[img], sel, 0]]
   ,
   Abort[];
   ]
  ]

Now we pre-calculate the positions of the seams:

out = CreateSeamcarveImageData[img];
Manipulate[SeamCarve[out, n], {n, 0, 500, 1}]

enter image description here

We can now interactively change the width without cropping essential features away. To give you a comparison, here I cut away 100 pixels (from 286 pixels to 186 pixels) using different methods:

enter image description here

To give you a better idea of what the seams are I show you the seam information:

Image[Rescale[out[[2]]]]
Colorize[out[[2]]]

enter image description here

Where (in the top figure) dark colors mean seams that will be removed first, while brighter seams are left for last. You can clearly see that the tower and the person are saved until the last. Using this code we can now crop the width of any picture.

Object removal

But we can extend this method: say that we want to remove an object from an image. We can use the same algorithm but now we use extra negative weight to the region we want to delete. Say we have the following image:

enter image description here

and we would like to remove the guy on the left. We create a mask that includes his shadow:

enter image description here

We update our code to include a negative mask:

ClearAll[ComputeEnergyFieldNegativeMask, CreateSeamcarveImageDataNegativeMask]
ComputeEnergyFieldNegativeMask[img_Image, mask_Image] := FoldList[#2 + MinFilter1[#1] &, ImageData[EnergyFunction[img]] - 10000 ImageData[mask]]
ComputeEnergyFieldNegativeMask[mat_List, mask_List] := ComputeEnergyFieldNegativeMask[Image[mat], Image[mask]]
CreateSeamcarveImageDataNegativeMask[img_Image, mask_Image] := Block[{maskdata, imagedata, dims, dimx, dimy, carveinfo, seam, 
   energyinfo}, (* removal *)
  If[ImageDimensions[img] == ImageDimensions[mask],
   imagedata = ImageData[img];
   maskdata = ImageData[ColorConvert[mask, "Grayscale"]];
   dims = {dimy, dimx} = Dimensions[imagedata, 2];
   carveinfo = ConstantArray[0, dims];
   PrintTemporary[Dynamic[Row[{"Calculating: ", i, "/", dimx}]]];
   Do[
    energyinfo = ComputeEnergyFieldNegativeMask[imagedata, maskdata];
    seam = FindSeam[energyinfo];
    carveinfo = 
     MapThread[FillNthPosition[#1, #2, i, 0] &, {carveinfo, seam}];
    imagedata = Carve[imagedata, seam];
    maskdata = Carve[maskdata, seam];
    ,
    {i, dimx}
    ];
   {img, carveinfo}
   ,
   Abort[];
   ]
  ]

Now trying out the code:

img = Import["beachpeeps.jpg"];
mask = Import["beachpeepsmask.png"];
AbsoluteTiming[out = CreateSeamcarveImageDataNegativeMask[img, mask];]
Manipulate[SeamCarve[out, n], {n, 0, 75, 1}]

enter image description here

Or a static comparison:

enter image description here

Object protection

In the same spirit, we can protect certain areas in the image that are important to us:

ClearAll[CreateSeamcarveImageDataPositiveMask, ComputeEnergyFieldPositiveMask]
ComputeEnergyFieldPositiveMask[img_Image, mask_Image] := FoldList[#2 + MinFilter1[#1] &, ImageData[EnergyFunction[img]] + 10000 ImageData[mask]]
ComputeEnergyFieldPositiveMask[mat_List, mask_List] := ComputeEnergyFieldPositiveMask[Image[mat], Image[mask]]
CreateSeamcarveImageDataPositiveMask[img_Image, mask_Image] := Block[{maskdata, imagedata, dims, dimx, dimy, carveinfo, seam, 
   energyinfo}, (* removal *)
  If[ImageDimensions[img] == ImageDimensions[mask],
   imagedata = ImageData[img];
   maskdata = ImageData[ColorConvert[mask, "Grayscale"]];
   dims = {dimy, dimx} = Dimensions[imagedata, 2];
   carveinfo = ConstantArray[0, dims];
   PrintTemporary[Dynamic[Row[{"Calculating: ", i, "/", dimx}]]];
   Do[
    energyinfo = ComputeEnergyFieldPositiveMask[imagedata, maskdata];
    seam = FindSeam[energyinfo];
    carveinfo = 
     MapThread[FillNthPosition[#1, #2, i, 0] &, {carveinfo, seam}];
    imagedata = Carve[imagedata, seam];
    maskdata = Carve[maskdata, seam];
    ,
    {i, dimx}
    ];
   {img, carveinfo}
   ,
   Abort[];
   ]
  ]

Where now our mask includes all the 3 persons in the image, including there shadows:

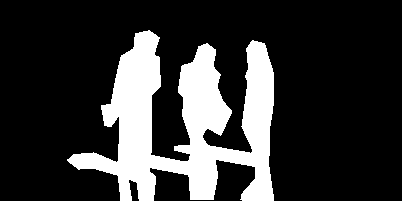
enter image description here

Again, we call our function:

img = Import["beachpeeps.jpg"];
mask = Import["beachpeepsmask2.png"];
AbsoluteTiming[out = CreateSeamcarveImageDataPositiveMask[img, mask];]
Manipulate[SeamCarve[out, n], {n, 0, 500, 1}]

Giving:

enter image description here

Or some static comparisons:

enter image description here

Final thoughts

For the energy-function we can use different functions, I used a simple (fast) GradientFilter, but other functions like ImageSaliencyFilter or EntropyFilter could also work. Seams now go from top to bottom, and the position of the seam changes at most 1 horizontal position per row of pixels, this can be changed without too much effort to be a bigger neighbourhood. Also this can be applied to videos but a 3-dimensional carve in space-time has to be calculated. Moreover, the energy function can be improved by including 'forward energy'. I can't wait for this functionality to be included in the Wolfram Language.

EDIT:
See my reply below, on how to implement forward energy.

P.S. I'm still confused why the guy has a skateboard on the beach...
POSTED BY: Sander Huisman
9 Replies
Sort By:

Extending

With some little extra code we can also extend an image:

$HistoryLength = 1;
ClearAll[MinFilter1, MinPosition, Neighbours, FindSeam, EnergyFunction, ComputeEnergyField, Carve, InjectPixel, SeamInject, FillNthPosition, CreateSeamcarveImageData, SeamCarve]
MinFilter1[x_List] := Min /@ Partition[x, 3, 1, {2, 2}, 1.0 10^6] (* same as MinFilter[x,1] but 10x faster *)
MinPosition[x_List] := First[Ordering[x, 1]] (* position of min element *)
Neighbours[n_Integer?Positive, len_Integer?Positive] := Which[n == 1, If[len > 1, {1, 2}, {1}],
  n == len, If[len > 1, {len, len - 1}, {1}],
  True, {n - 1, n, n + 1}
  ]
FindSeam[mat_List?MatrixQ] := Module[{dimx, dimy, seam, neighbours, values, newpos, ii},
  {dimy, dimx} = Dimensions[mat];
  seam = ConstantArray[-1, dimy];
  seam[[-1]] = MinPosition[mat[[-1]]];
  Do[
   neighbours = Neighbours[seam[[ii + 1]], dimx];
   values = mat[[ii, neighbours]];
   newpos = neighbours[[MinPosition[values]]];
   seam[[ii]] = newpos
   ,
   {ii, dimy - 1, 1, -1}
   ];
  seam
  ]
EnergyFunction[img_Image] := GradientFilter[img, 1, Method -> "ShenCastan"]
ComputeEnergyField[img_Image] := FoldList[#2 + MinFilter1[#1] &, ImageData[EnergyFunction[img]]]
ComputeEnergyField[mat_List] := ComputeEnergyField[Image[mat]]
Carve[mat_List?ArrayQ, seam_List] := MapThread[Delete, {mat, seam}, 1]
FillNthPosition[x_List, n_Integer?Positive, fill_, empty_: 0] := Block[{pos, out},
  out = x;
  pos = Position[out, empty, {1}, n, Heads -> False];
  out[[pos[[n]]]] = fill;
  out
  ]
CreateSeamcarveImageData[img_Image] := Block[{imagedata, dims, dimx, dimy, carveinfo, seam, energyinfo},
  imagedata = ImageData[img];
  dims = {dimy, dimx} = Dimensions[imagedata, 2];
  carveinfo = ConstantArray[0, dims];
  PrintTemporary[Dynamic[Row[{"Calculating: ", i, "/", dimx}]]];
  Do[
   energyinfo = ComputeEnergyField[imagedata];
   seam = FindSeam[energyinfo];
   carveinfo = 
    MapThread[FillNthPosition[#1, #2, i, 0] &, {carveinfo, seam}];
   imagedata = Carve[imagedata, seam];
   ,
   {i, dimx}
   ];
  {img, carveinfo}
  ]
SeamCarve[{img_Image, carveinfo_List}, n_Integer?NonNegative] := Block[{imgdata, pick, sel, m},
  imgdata = ImageData[img];
  If[Dimensions[imgdata, 2] == Dimensions[carveinfo],
   m = Clip[n, {0, Length[carveinfo[[1]]] - 1}];
   sel = UnitStep[m - carveinfo];
   Image[Pick[ImageData[img], sel, 0]]
   ,
   Abort[];
   ]
  ]
InjectPixel[lst_List?ArrayQ, index_Integer?Positive] := Module[{len},
  len = Length[lst];
  If[index == 1,
   Prepend[lst, First[lst]]
   ,
   Insert[lst, Mean[lst[[index - 1 ;; index]]], index]
   ]
  ]
SeamInject[mat_List?ArrayQ, seam_List] := MapThread[InjectPixel, {mat, seam}]
SeamCarve[{img_Image, carveinfo_List}, n_Integer?NonPositive] := Block[{imgdata, m, ci, seam},
  imgdata = ImageData[img];
  If[Dimensions[imgdata, 2] == Dimensions[carveinfo],
   m = Clip[-n, {0, Length[carveinfo[[1]]] - 1}];
   ci = carveinfo;
   Do[
    seam = Position[ci, i, {2}][[All, 2]];
    imgdata = SeamInject[imgdata, seam];
    ci = MapThread[Insert[#1, i, #2] &, {ci, seam}];
    ,
    {i, m}
    ];
   Image[imgdata]
   ,
   Abort[];
   ]
  ]

Now we can calculate the seams:

img = Import["tower.png"];
AbsoluteTiming[out = CreateSeamcarveImageData[img];]
Manipulate[SeamCarve[out, n], {{n, 0}, -100, 100, 1}]

enter image description here

Note that negative values are much slower to calculate; new data has to be created seam-by-seam. While for removal one can just delete values at once (I used Pick which is very fast). Basically we insert seam where we previously would have deleted them. This works reasonably well for small extensions, but not for large insertions, moreover, it is limited by the original width of the image. So one can extend the image at most the width of the original resulting in an image that has twice the width.

Here is a static comparison:

enter image description here

where the number in front is the number of removed seams (negative meaning injected seams).

Attachments:
POSTED BY: Sander Huisman

Forward energy

As discussed in various papers, sometimes the results are better when considering 'forward energy' i.e. one does not only look at the energy at the position of the seam, but also to the future gradient. So the energy is the current gradient but also the gradient if one were to remove the seam (which could create a sharper gradient than the original). This can be implemented as follows:

ClearAll[MinPosition, Neighbours, FindSeam, EnergyFunction, ComputeEnergyFieldForward, Carve, FillNthPosition, CreateSeamcarveImageData, SeamCarve]
MinPosition[x_List] := First[Ordering[x, 1]] (* position of min element *)
Neighbours[n_Integer?Positive, len_Integer?Positive] := Which[n == 1, If[len > 1, {1, 2}, {1}],
  n == len, If[len > 1, {len, len - 1}, {1}],
  True, {n - 1, n, n + 1}
  ]
FindSeam[mat_List?MatrixQ] := Module[{dimx, dimy, seam, neighbours, values, newpos, ii},
  {dimy, dimx} = Dimensions[mat];
  seam = ConstantArray[-1, dimy];
  seam[[-1]] = MinPosition[mat[[-1]]];
  Do[
   neighbours = Neighbours[seam[[ii + 1]], dimx];
   values = mat[[ii, neighbours]];
   newpos = neighbours[[MinPosition[values]]];
   seam[[ii]] = newpos
   ,
   {ii, dimy - 1, 1, -1}
   ];
  seam
  ]
EnergyFunction[img_Image] := GradientFilter[img, 1, Method -> "ShenCastan"]
ComputeEnergyFieldForward[img_Image] := Module[{\[Iota], m, \[Kappa], \[Lambda], len, t1, t2, t3},
  \[Iota] = ImageData[EnergyFunction[img]];
  m = ConstantArray[-1.0, Dimensions[\[Iota]]];
  m[[1]] = \[Iota][[1]];
  len = Length[First[\[Iota]]];
  Do[
   \[Kappa] = Prepend[Append[\[Iota][[j - 1]], \[Iota][[j - 1, -1]]], \[Iota][[j - 1, 1]]];
   \[Lambda] = Prepend[Append[\[Iota][[j]], \[Iota][[j, -1]]], \[Iota][[j, 1]]];
   t1 = Partition[m[[j - 1]], 3, 1, {2, 2}, 1.0 10^6];
   t2 = If[len >= 3, Abs@ListCorrelate[{-1, 0, 1}, \[Lambda]], ConstantArray[0.0, len]];
   t3 = If[len >= 1, Transpose[{Most@Abs[\[Kappa][[2 ;;]] - \[Lambda][[;; -2]]], 
       ConstantArray[0.0, len], 
       Rest@Abs[\[Kappa][[;; -2]] - \[Lambda][[2 ;;]]]}],
     ConstantArray[0.0, len]];
   m[[j]] = Min /@ (t1 + t2 + t3);
   , {j, 2, Length[\[Iota]]}
   ];
  m
  ]
ComputeEnergyFieldForward[mat_List] := ComputeEnergyFieldForward[Image[mat]]
Carve[mat_List?ArrayQ, seam_List] := MapThread[Delete, {mat, seam}, 1]
FillNthPosition[x_List, n_Integer?Positive, fill_, empty_: 0] := Block[{pos, out},
  out = x;
  pos = Position[out, empty, {1}, n, Heads -> False];
  out[[pos[[n]]]] = fill;
  out
  ]
CreateSeamcarveImageData[img_Image] := Block[{imagedata, dims, dimx, dimy, carveinfo, seam, energyinfo},
  imagedata = ImageData[img];
  dims = {dimy, dimx} = Dimensions[imagedata, 2];
  carveinfo = ConstantArray[0, dims];
  PrintTemporary[Dynamic[Row[{"Calculating: ", i, "/", dimx}]]];
  Do[
   energyinfo = ComputeEnergyFieldForward[imagedata];
   seam = FindSeam[energyinfo];
   carveinfo = MapThread[FillNthPosition[#1, #2, i, 0] &, {carveinfo, seam}];
   imagedata = Carve[imagedata, seam];
   ,
   {i, dimx}
   ];
  {img, carveinfo}
  ]
SeamCarve[{img_Image, carveinfo_List}, n_Integer?NonNegative] := Block[{imgdata, pick, sel, m},
  imgdata = ImageData[img];
  If[Dimensions[imgdata, 2] == Dimensions[carveinfo],
   m = Clip[n, {0, Length[carveinfo[[1]]] - 1}];
   sel = UnitStep[m - carveinfo];
   Image[Pick[ImageData[img], sel, 0]]
   ,
   Abort[];
   ]
  ]

Here are the differences:

enter image description here

As you can see it prevents some of the sharp edges that are present in the original implementation.

Another example is with this bench photo (left original method, right forward energy):

enter image description here

Again, the image stays smoother without any sharp edges being created. The first 150 pixels that are removed can also be compared:

enter image description here

In the forward energy case (bottom) you can see that the seams are more spread-out, which prevents gradients from being created.

Attachments:
POSTED BY: Sander Huisman

Extremely Impressive. Upvoted. thanks for sharing.
POSTED BY: Ali Hashmi

Thanks Ali.
POSTED BY: Sander Huisman

Amazing !
POSTED BY: Thibaut Jonckheere

Thanks!
POSTED BY: Sander Huisman

enter image description here - another post of yours has been selected for the Staff Picks group, congratulations! We are happy to see you at the top of the "Featured Contributor" board. Thank you for your wonderful contributions, and please keep them coming!
POSTED BY: EDITORIAL BOARD

Thanks!
POSTED BY: Sander Huisman

Based on the wikipedia entry of seam carving. The algorithm can also be adjusted to extend image (negative cropping) using seam insertion rather than seam carving. (see below!). At the moment the algorithm is not very fast but could be improved using Compile (I think).

POSTED BY: Sander Huisman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard