Cloud

Consider all possible equilateral pentagons in the plane, including self-intersecting polygons. If we only care about shapes of pentagons, we may as well mod out by translations and rotations, which we can achieve by, say, fixing vertex 2 to be $(0,0)$ and vertex 3 to be $(1,0)$. The two adjacent sides to this fixed edge will form angles $\theta_1$ and $\theta_2$, so vertex 1 and vertex 4 move on the unit circles centered on $(0,0)$ and $(1,0)$. Now, for each value of $(\theta_1,\theta_2)$, there are either 0, 1, 2, or infinitely many possible locations for the fifth vertex depending on whether the distance between vertices 1 and 4 is greater than 2, equal to 2, or strictly between 0 and 2, or equal to 0 (when vertices 1 and 4 coincide, vertex 5 can be anywhere on the unit circle centered at vertex 1/4).

Here's an animation showing some possible configurations, with a blue pentagon and a red pentagon when there are two solutions and the four edges shown in black when there are no solutions:

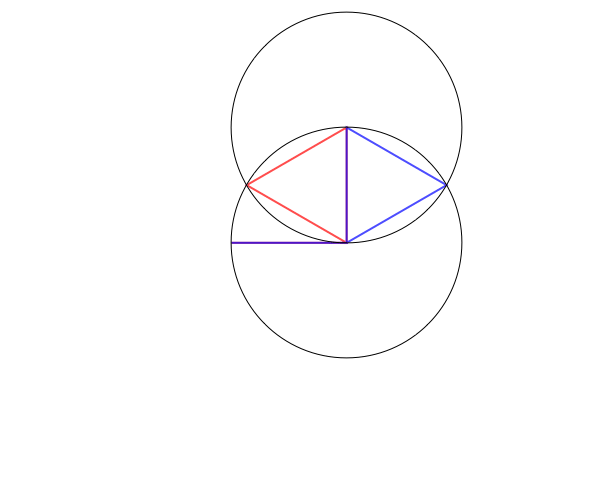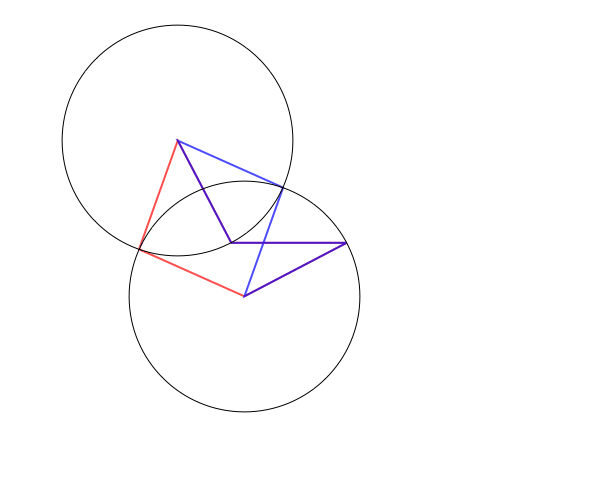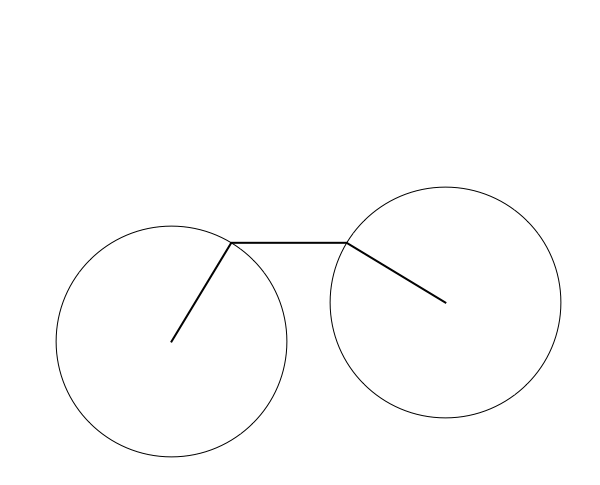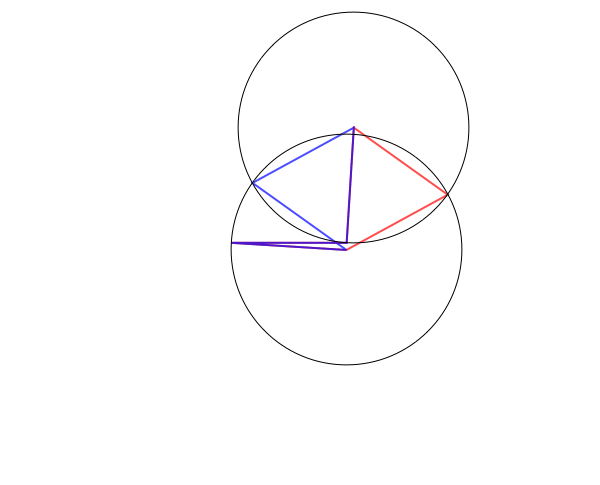
Now, since there are two free parameters and (generically), finally many points for each parameter, it's natural to guess that the space of all possible planar pentagons is a surface; indeed, Havel, Kamiyama, and Kapovich--Millson have showed that it's an orientable surface of genus 4.

In an attempt to visualize this space, I took the coordinates $(x_1,y_1)$, $(x_4,y_4)$, and $(x_5,y_5)$ of vertices 1, 4, and 5, interpreted as points $(x_1, y_1, x_4, y_4, x_5, y_5)$ in $\mathbb{R}^6$, sampled 13,940 points, and then projected to the 3-dimensional linear subspace of maximum variance (i.e., the span of the singular vectors corresponding to the three highest singular values). This is in some sense kind of a stupid thing to do, because all of the singular values are large, so this is still projecting away a lot of information. Still, it makes for an interesting animation!

Here's the code.

First of all, a function which turns $(\theta_1,\theta_2)$ into the four obvious vertices and a function which returns the two possible locations for the firfth vertex (when it exists):

FourPointConfiguration[?1_, ?2_] := {{Cos[?1], 
    Sin[?1]}, {0, 0}, {1, 
    0}, {1, 0} + {Cos[?2], Sin[?2]}};
FifthPoints[?1_, ?2_] := {x, y} /. # & /@ 
   Solve[Norm[{x, y} - {Cos[?1], Sin[?1]}] == 1 && 
     Norm[{x, y} - {1 + Cos[?2], Sin[?2]}] == 1, {x, y}];

Also, a function to check when there is a fifth vertex at all (notice that this excludes the case when there is exactly one solution, which in practice isn't going to matter so much:

LegalConfiguration[?1_, ?2_] := 
      Norm[FourPointConfiguration[?1, ?2][[1]] - 
         FourPointConfiguration[?1, ?2][[-1]]] < 2;

Now, when vertices 1 and 4 coincide, we get a whole circle's worth of possible locations for the fifth vertex. Notice that this only happens when $(\theta_1,\theta_2) = (\pi/3,2\pi/3)$ or $(5\pi/3,4\pi/3)$. Here's a function which returns the pentagons corresponding to $n$ equally-spaced points on these two circles:

SampleBadPentagons[n_] := 
  Join[ParallelTable[
    Flatten[Append[
      FourPointConfiguration[?/3., 2 ?/3.][[{1, 4}]], 
      FourPointConfiguration[?/3., 2 ?/3.][[
        4]] + {Cos[?], Sin[?]}], 1], {?, 0, 
     2 ? - 2 ?/n, 2 ?/n}], 
   ParallelTable[
    Flatten[Append[
      FourPointConfiguration[5 ?/3., 4 ?/3.][[{1, 4}]], 
      FourPointConfiguration[5 ?/3., 4 ?/3.][[
        4]] + {Cos[?], Sin[?]}], 1], {?, 0, 
     2 ? - 2 ?/n, 2 ?/n}]];

Now, here's a function which generates $\theta_1$ and $\theta_2$, each as $n$ evenly-spaced points on the circle (so $n^2$ total points), throws away the values which don't produce pentagons, builds both possible pentagons for each legal pair $(\theta_1,\theta_2)$, and then tacks some of the weird pentagons from the previous function. I did some playing around and found that taking $n/3$ points from each of the two weird circles of pentagons seems to give about the same density of points.

SamplePentagonSpace[n_] := Module[{angles, legalAngles},
   angles = 
    Flatten[Table[{?1, ?2}, {?1, 0., 
       2 ? - 2 ?/n, 2 ?/n}, {?2, 0., 
       2 ? - 2 ?/n, 2 ?/n}], 1];
   legalAngles = Select[angles, LegalConfiguration @@ # &];
   Join[Flatten[
     ParallelTable[
      Flatten[Append[
          FourPointConfiguration[legalAngles[[i, 1]], 
            legalAngles[[i, 2]]][[{1, 4}]], #]] & /@ 
       FifthPoints[legalAngles[[i, 1]], legalAngles[[i, 2]]], {i, 1, 
       Length[legalAngles]}], 1], SampleBadPentagons[Floor[n/3]]]
   ];

With all that code written, we now just need to sample a bunch of points

pentagonsamplesSmall = SamplePentagonSpace[100];

...and then project and visualize:

DynamicModule[{cols = RGBColor /@ {"#86EE60", "#2B3752"}, svd, data},
 svd = SingularValueDecomposition[pentagonsamplesSmall, 3];
 data = Manipulate[
   ListPointPlot3D[svd[[1]].svd[[2]], BoxRatios -> {1, 1, 1}, 
    ImageSize -> 540, SphericalRegion -> True, Boxed -> False, 
    Axes -> None, 
    PlotStyle -> Directive[PointSize[.007], Opacity[.3], cols[[1]]], 
    Background -> cols[[-1]], 
    ViewPoint -> 3 {Cos[?], Sin[?], .1}, 
    ViewVertical -> {0, 0, 1}], {?, 0, 2 ?}]
 ]