Introduction
This project is to create a series of interactive macroeconomic models using Mathematica. The underlying motive is to help many instructors in the college level economics courses motivate and engage their students with some advanced computational technology.
As a starter, I build and replicate the Keynesian aggregate demand model (with some varying specifications) that we can use in the classroom to demonstrate some dynamic features of the model.
Building a simple Keynesian AD model
The mathematical structure of the Keynesian AD model is quite simple. Let us suppose that the aggregate demand ("AD") in our simple model economy consists of household consumption expenditure ("C") and private business investment spending ("PBI"), and that the household consumption expenditure can be further decomposed into two parts, one autonomous part of consumption("Subscript[c, 0]") and the other variable part of consumption.
If we assume that there is a statistically significant and stable correlation between households' average consumption spending habit ("Subscript[c, 1]") and their income ("Y"), then the variable part of consumption becomes a function of households' income ("Subscript[c, 1]Y "). Based upon this reasoning, we can hypothesize the following behavioral equation that constitutes the aggregate demand, that is,
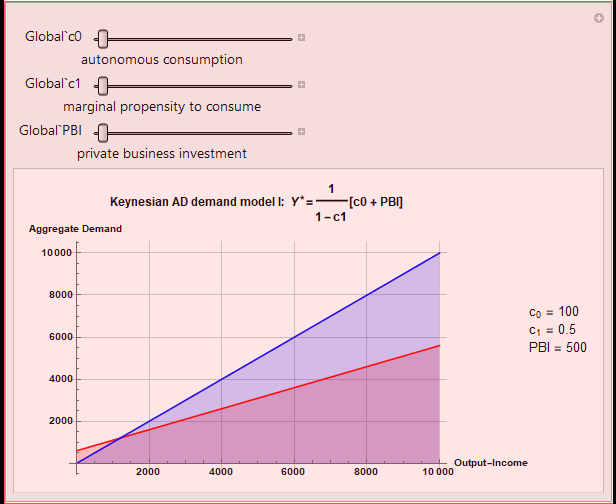
AD=Subscript[c, 0]+Subscript[c, 1]Y+PBI
Solve[Y ==Subscript[c, 0]+Subscript[c, 1]Y+PBI,Y]
The syntax for creating an interactive model is as follow:
Manipulate[
Row[{Plot[{c0+c1*Y +PBI,Y} ,{Y,0,10000},GridLines->Automatic,AxesLabel->{"Output-Income","Aggregate Demand"},PlotStyle->{Red,Blue},LabelStyle->Directive[Black,Bold], Filling->Bottom,PlotLabel->"Keynesian AD demand model I",ImageSize->500],
Column[{
Style["Subscript[c, 0] = "<>ToString[c0],FontFamily->"Helvetica"],
Style["Subscript[c, 1] = "<>ToString[c1],FontFamily->"Helvetica"],
Style[ "PBI = "<>ToString[PBI],FontFamily->"Helvetica"]
}]}],
{c0,100,1000,50},Item["autonomous consumption",Alignment->Center],
{c1,0.5,0.9,0.05},Item["marginal propensity to consume",Alignment->Center],
{PBI,500,1000,100},Item["private business investment",Alignment->Center],SaveDefinitions->True]
Extending the baseline Keynesian AD model with the government sector
If government is present and if it adopts a particular tax policy that is a combination of the lump-sum tax ("Subscript[t, 0]") and marginal tax rate ("Subscript[t, 1]"), the household consumption expenditure and the aggregate demand needs to be modified:
AD=Subscript[c, 0]+Subscript[c, 1]*(Y-t0-t1 Y+TR)+PBI +G
Solve[Subscript[c, 0]+Subscript[c, 1]*(Y-t0-t1 Y+TR)+PBI+G==Y,Y]
Interactive model Manipulate[
Row[{Plot[{c0+c1*(Y-t0-t1 Y+TR) +PBI+G,Y} ,{Y,0,10000},GridLines->Automatic,AxesLabel->{"Output-Income","Aggregate Demand"},PlotStyle->{Red,Blue},LabelStyle->Directive[Black,Bold], Filling->Bottom,PlotLabel->"Keynesian AD demand model IV: Y^*=1/(1-c1(1-t))*[c0-c1*t0+c1*TR+PBI+G]",ImageSize->500],
Column[{
Style["Subscript[c, 0] = "<>ToString[c0],FontFamily->"Helvetica"],
Style["Subscript[c, 1] = "<>ToString[c1],FontFamily->"Helvetica"],
Style[ "PBI = "<>ToString[PBI],FontFamily->"Helvetica"],
Style[ "G = "<>ToString[G],FontFamily->"Helvetica"],
Style[ "Subscript[t, 0] = "<>ToString[t0],FontFamily->"Helvetica"],
Style[ "Subscript[t, 1] = "<>ToString[t1],FontFamily->"Helvetica"],
Style[ "TR = "<>ToString[TR],FontFamily->"Helvetica"]
}]}],
{c0,100,500,50},Item["autonomous consumption",Alignment->Center],
{c1,0.5,0.8,0.05},Item["marginal propensity to consume",Alignment->Center],
{PBI,500,1000,100},Item["private business investment",Alignment->Center],
{G,500,1000,100},Item["government expenditure",Alignment->Center],
{t0,100,500,50},Item["lump-sum tax",Alignment->Center],
{t1,0.1,0.8,0.05},Item["marginal tax rate",Alignment->Center],
{TR,100,400,100},Item["transfer income",Alignment->Center],SaveDefinitions->True]
The Keynesian AD model with the foreign sector
If the economy is open to international trade, the volume of export and import also affects domestic aggregate demand. If we define "X" as the total volume of export, and "M" as the total volume of import, Subscript[c, 2] Y can approximate the volume of total import, which is a function of marginal propensity to consume for imported goods and the level of income. In this case, our new solution for the AD equation is:
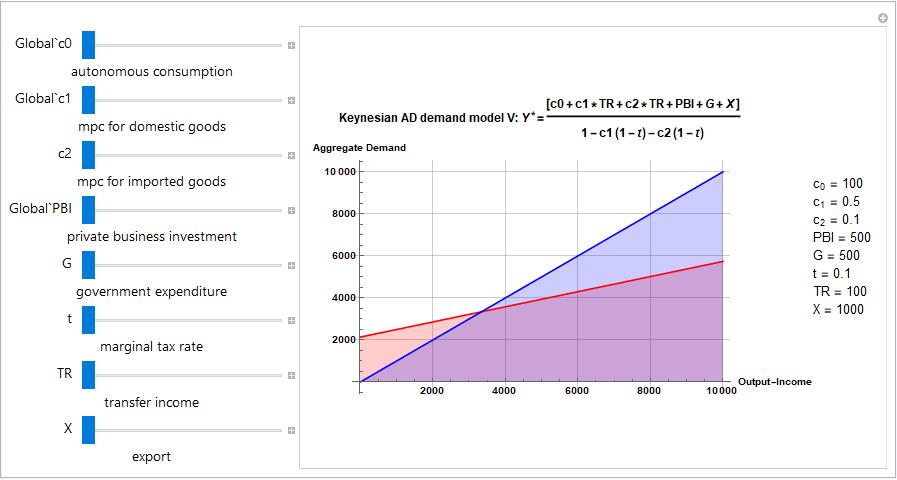
AD=Subscript[c, 0]+(Subscript[c, 1]-Subscript[c, 2])*(Y-t Y+TR)+PBI +G +X
Solve[Subscript[c, 0]+(Subscript[c, 1]-Subscript[c, 2])*(Y-t Y+TR)+PBI +G +X==Y,Y]
Interactive model Manipulate[
Row[{Plot[{c0+(c1-c2)*(Y-t Y+TR)+PBI+G+X,Y} ,{Y,0,10000},GridLines->Automatic,AxesLabel->{"Output-Income","Aggregate Demand"},PlotStyle->{Red,Blue},LabelStyle->Directive[Black,Bold], Filling->Bottom,PlotLabel->"Keynesian AD demand model V: Y^*=[c0+c1*TR+c2*TR+PBI+G+X]/(1-c1(1-t)-c2(1-t))",ImageSize->500],
Column[{
Style["Subscript[c, 0] = "<>ToString[c0],FontFamily->"Helvetica"],
Style["Subscript[c, 1] = "<>ToString[c1],FontFamily->"Helvetica"],
Style[ "Subscript[c, 2] = "<>ToString[c2],FontFamily->"Helvetica"],
Style[ "PBI = "<>ToString[PBI],FontFamily->"Helvetica"],
Style[ "G = "<>ToString[G],FontFamily->"Helvetica"],
Style[ "t = "<>ToString[t],FontFamily->"Helvetica"],
Style[ "TR = "<>ToString[TR],FontFamily->"Helvetica"],
Style[ "X = "<>ToString[X],FontFamily->"Helvetica"]
}]}],
{c0,100,500,50},Item["autonomous consumption",Alignment->Center],
{c1,0.5,0.8,0.05},Item["mpc for domestic goods",Alignment->Center],
{c2,0.1,0.6,0.05},Item["mpc for imported goods",Alignment->Center],
{PBI,500,1000,100},Item["private business investment",Alignment->Center],
{G,500,1000,100},Item["government expenditure",Alignment->Center],
{t,0.1,0.8,0.1},Item["marginal tax rate",Alignment->Center],
{TR,100,400,100},Item["transfer income",Alignment->Center],
{X,1000,5000,100},Item["export",Alignment->Center],SaveDefinitions->True]
Next steps
The project in this notebook is to build an interactive Keynesian aggregate demand model. With these interactive models, I hope that our students will be able to see the likely effect of the change in the parameter and to better understand the structure, dynamics, and implication of the original Keynesian aggregate demand model. I also hope that many instructors in macroeconomic courses find some of these models pedagogically useful in motivating and enhancing our students effective learning.
The next step in this Mathematica modeling exercise is to (1) show how we can estimate the realistic (range of) values of parameters based upon historical data for the U.S., and (2) to modify the models in a dynamic setting by introducing difference/differential equations. For the modeling building purpose, most of the parameters used in the above are chosen arbitrarily. One important step forward is to conduct some additional statistical analyses based upon the US historical data in order to obtain more realistic parameter values. Another way of improving this project is to introduce time lags among some variables, so that we can transform the aggregate demand equations into difference/differential equations. If successful, the new models will show more complex patterns of dynamic adjustments.
|