Dear all,
I do hope that this is not off-topic, but I would like to make the remark that when the evolution of magnetization is described by the respective differential equation (instead of a difference equation), this system can be solved in an analytic way easily:
dim = 10; (* number of magnets: *)
(* definition of the before mentioned "update matrix": *)
mat = Normal@
SparseArray[{Band[{1, 1}] -> -2, Band[{1, 2}] -> 1, Band[{2, 1}] -> 1}, {dim, dim}];
mat[[1, 1]] = mat[[dim, dim]] = -1;
mat // MatrixForm
Then we have equation : d magVec / dt == mat.magVec,
and mat.magVec gives the desired terms (all constants are set to 1) :
(* general magnetic vector: *)
magVec = Table[m[n], {n, 1, dim}];
(* 'd/dt' on lhs is just "symbolic" to show the system of equations! *)
Thread[(d /dt) magVec == mat.magVec] // MatrixForm

(* solution matrix in time 't': Exp[mat t], i.e.: *)
expMat = MatrixExp[mat t];
(* initial condition - magnetic state at t==0: *)
startMagnVect = Prepend[ConstantArray[0, dim - 1], 1];
(* {1, 0, 0, 0, 0, 0, 0, 0, 0, 0} *)
(* analytical solution: *)
mgt = expMat.startMagnVect;
mgtN = N[mgt];
Plot of the result, i.e. magnetization in time:
labels = Style[#, 20] & /@ Range[dim];
Plot[mgtN, {t, 0, 30}, ImageSize -> 600, PlotRange -> All, PlotLabels -> Placed[labels, Above]]
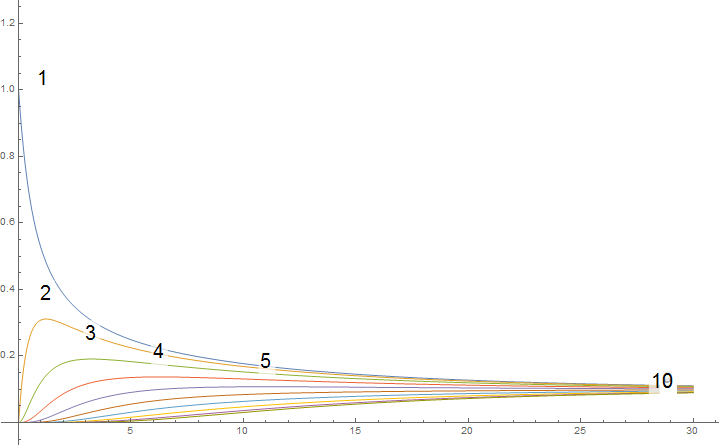
The sum of all solutions is alway '1' - as correctly claimed by @Hans Dolhaine :
Total@mgt // Simplify
(* Out: 1 *)
And all limits seem to be the same - consequently '1/dim', e.g.:
Limit[mgt[[4]], t -> Infinity]
(* Out: 1/10 *)
The dimensionality of this method is quite limited; if you go beyond dim = 10; the calculation time explode. But it seems to show the general behaviour, though.