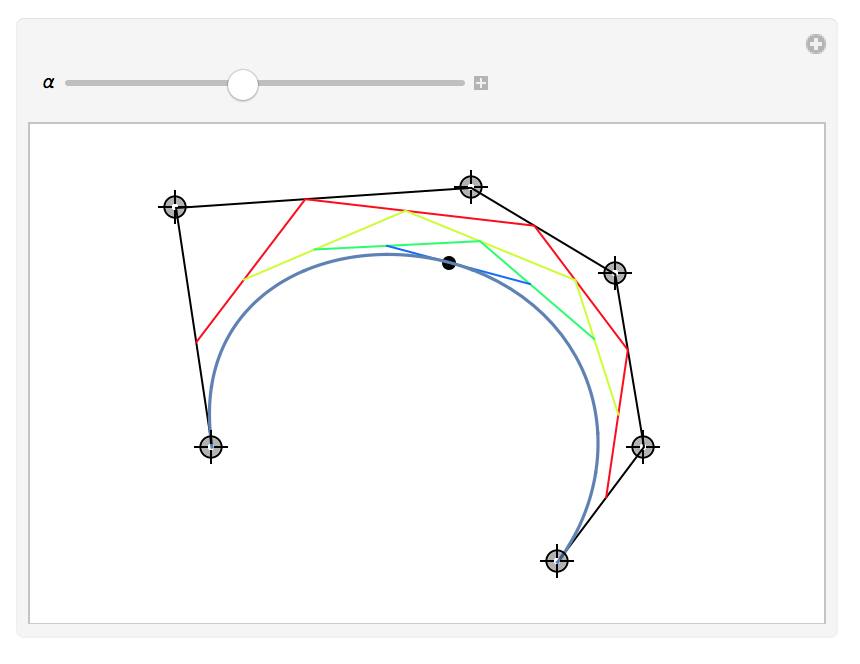
Or do it yourself, the construction is quite easy:
Clear[Smoothed, CreateGraphics]
Smoothed[pts_List, \[Alpha]_?
NumericQ] := {1 - \[Alpha], \[Alpha]}.# & /@ Partition[pts, 2, 1]
CreateGraphics[pts_List, \[Alpha]_] :=
Module[{sublines, smooth, \[Theta], gr},
sublines = NestList[Smoothed[#, \[Alpha]] &, pts, Length[pts] - 2];
smooth = Nest[Smoothed[#, \[Theta]] &, pts, Length[pts] - 1];
sublines =
Riffle[Line /@ sublines, Hue /@ Range[0, 1, 1/(Length[pts] - 1)]];
gr = ParametricPlot[smooth, {\[Theta], 0, 1}];
Show[{Graphics[{sublines, PointSize[Large],
Point[smooth /. \[Theta] -> \[Alpha]]}], gr},
PlotRange -> {{-2, 3}, {-1, 2}}]
]
Manipulate[
CreateGraphics[
pt, \[Alpha]], {{pt, {{-1, 0}, {-0.8, 1.6}, {0.8, 1.8}, {1.8,
1.2}, {2, 0}, {1.4, -0.8}}}, Locator,
LocatorAutoCreate -> {3, 8}}, {{\[Alpha], 0.3}, 0, 1}]
giving: