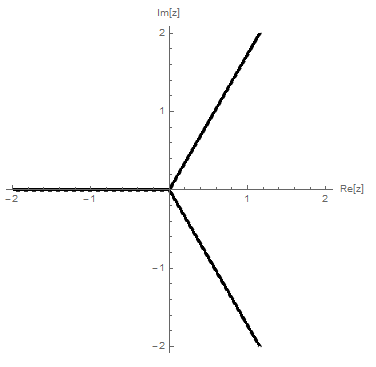
In this case, ContourPlot can do the trick.

     f[z_] := Log[z^3];
     With[{z = x + I y}, ContourPlot[Im[f[z]], {x, -2, 2}, {y, -2, 2}, ClippingStyle -> Automatic, ExclusionsStyle -> {Black, Dashed}, 
     Axes -> True, Frame -> False, Contours -> 1, ContourShading -> None,ContourStyle -> None, AxesLabel -> {"Re[z]", "Im[z]"}]]

Very cool! Where/how did you find the function?

That is the perfect code I needed. Thank you so much!!! and thanks to everyone. You are all so smart and nice. best wishes

thank you so much Mr Huisman.

I am aware of the arbitrary way branch cuts can be defined.

Commonly though the Log[Z] function is defined on the principal branch with the branch cut being the origin and the negative real axis.

I used your code and graphed Log[Z] and it appears the branch is at y=0 and x<=1.

Why is this?

I thought it should be at y=0 and x<=0.

thanks in advance best wishes

i do not wish for a Riemann surface representation...just a 2d plot of the branch cuts like i have seen in Maple

How to you determine the branch lines? I believe they are somewhat arbitrary. (Correct me if I'm wrong!) For standard functions in Mathematica the function Help pages generally tell you how the branch lines are chosen. For arbitrary functions you are relatively free to pick the paths yourself.

If the function you are looking at has a small finite number of critical points or branch points then it can be represented on a Riemann surface and has no branch lines at all. My Presentations application has Multivalues routines that allows one to plot a function on a Riemann surface. The function value is represented by a vector attached to a Locator point. As you drag the locator around the vector will change but it is always smooth and single valued. For the Sqrt[z] you can drag it around the origin without any discontinuities but you have to go around twice to return the same value. You have traversed different portions of the Riemann surface.