In my opinion, there are two errors in your code. First, the interval for $r$ must be written correctly in the form specified by the documentation:

In your code $r_{max}$ must be a number, but not a variable expression dependent of $\Theta$ and $z$.

Second, the expression for RegionPlot3D[] must be an inequality. So, by providing these two corrections and fixing $r_{max}$ to value $1.2 Sqrt[\pi/4]$, the code

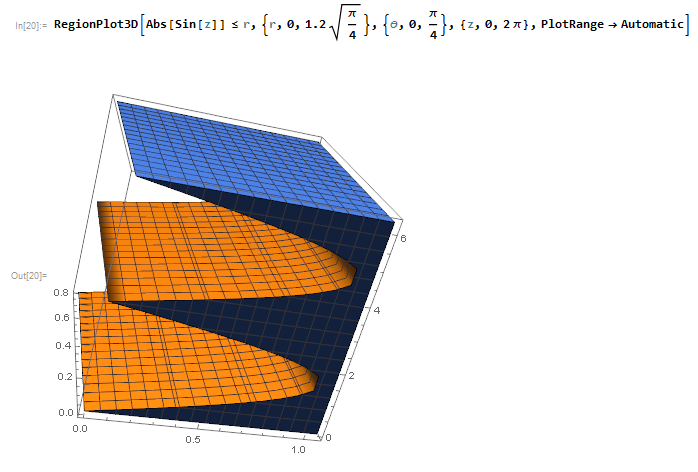
RegionPlot3D[
 Abs[Sin[z]] <= r, {r, 0, 1.2 Sqrt[\[Pi]/4]}, {\[Theta], 0, \[Pi]/
  4}, {z, 0, 2 \[Pi]}, PlotRange -> Automatic]

generates the following graph:

Sure, the code becomes more interesting if we use the function Manipulate[]:

Manipulate[
 RegionPlot3D[
  Abs[Sin[z]] <= r, {r, 0, rmax}, {\[Theta], 0, \[Pi]/4}, {z, 0, 
   2 \[Pi]}, PlotRange -> Automatic], {rmax, 0.1, 3}]