Hi, Danny, thanks for taking some time to respond. I think the code is already out there to satisfy all of your demands, but admittedly I have not been explaining the calculations in any detail. Let's aim for closer to article quality with this post, and see if we can convince ourselves that Mathematica function InverseSeries can be improved on a wide range of inputs. We have not two, but three distinct methods to compare!
Statement of the Problem & Variable Parameters
We start with a power series expansion
$$ z = x^m+\sum_{i>m}^{\infty}c_i \; x^i$$
with
$m$ defined as the leading power. Without loss of generality we have already assumed that the coefficient of the leading term
$c_m$ can be set to
$1$ by change of the
$x$ variable. We seek a solution
$x=f(y(z))$, which expands in whole powers of
$y(z)$,
$$ x = y + \sum_{i>1}^{n+1} f_{i}(\mathbf{c}) y^i, $$
with
$n$ defined as truncation parameter and
$f_{i}(\mathbf{c})$
is in general a complicated, but well structured function of the expansion coefficients
$\mathbf{c}= ( c_i:i\in1,2,\ldots )$.
It's worthwhile to mention up front that the
$f_{i}(\mathbf{c})$
for case
$m=1$
have already been explored in numerous outlets including Mathworld, Abramowitz and Stegun, and the OEIS. From the OEIS entry: "The sequence of row lengths is A000041(n) (partition numbers)", which gives us an expectation regarding the number of terms in each
$f_i(\mathbf{c})$. This same row-length feature is shared by the triangle for
$m=2$, which I added to the OEIS while working on physics problems, including planetary motion, A276738. This is an important feature at any
$m$, which we will return to shortly. All functions will take parameters
$m$ and
$n$ as input and return as output the expansion
$x(y(z))$, which inverts the
$z(x)$ expansion. Our complexity expectations are as follows:
- Changing
$m$ does not change complexity class
- Changing
$n$ explores complexity class
$\mathcal{O}(p(n))$, where the
$p(n)$ are the partition numbers, listed in A000041.
Using the built-in Function
Let's take the code from above MmaExpand, and break it apart into two functions
MmaSeries[n_, m_] := Series[f[x], {x, 0, n + m}] /.
Join[{f[0] -> 0, (D[f[x], {x, m}] /. x -> 0) -> (m!)}, (D[f[x], {x, #}] /. x -> 0) -> 0 & /@
Range[1, m - 1], ((D[f[x], {x, #}] /. x -> 0) -> #! c[#]) & /@
Range[m + 1, n + m]]
MmaExpand[n_, m_] := Expand[Refine[Normal[InverseSeries[MmaSeries[n, m]]] /. x -> y^m, y > 0]]
The first function generates a series and the second function--It's magic to me, slower magic--generates the inverse expansion. Additionally we utilize the small
$x$ limit where
$z \approx x^m$ to prove that the solution is an expansion in integer powers of
$y=z^{1/m}$. This is easy to see once you have studied the multinomial method in the next section. For now we need to run a few critical tests:
AbsoluteTiming[
RowLengthTest = MatrixForm[Function[{m},
Length /@ (Coefficient[MmaExpand[8, m], y, #] /. Plus -> List & /@
Range[3, 8])] /@ Range[5]
]]
AbsoluteTiming[ Outer[Coefficient[ Expand[Normal@MmaSeries[4, #1] /. x -> MmaExpand[4, #1]],
y, #2] &, Range[5], Range[5] ] // MatrixForm ]

Both are maps where index
$m=1,2,3,4,5...$ corresponds to a row. First, we see the number of terms is the partition numbers, as expected. Next in the identity matrix, we see up to power
$y^5$ substitution of the inverse series into the series cancels all terms other than
$y^m=z$, as required. Let's take for granted that the only problem is time. We obtain timing statistics by mapping over
$m$ and
$n$
t1=Outer[AbsoluteTiming[MmaExpand[#2, #1]][[1]] &, Range[5], Range[10]]
Out[] = {
{0.00795752, 0.0104603, 0.00681345, 0.00671655, 0.0118878, 0.022436, 0.0632026, 0.159615, 0.443813, 1.42085},
{0.00181332, 0.00326319, 0.00738307, 0.0140106, 0.0274177, 0.0521328, 0.118843, 0.26841, 0.684693, 1.9761},
{0.00188818, 0.00317625, 0.00734353, 0.013728, 0.0268191, 0.051075, 0.116821, 0.266313, 0.681015, 1.92303},
{0.00231411, 0.00382979, 0.0077761, 0.0146602, 0.0272598, 0.0552915, 0.119205, 0.270802, 0.690533, 1.93577},
{0.00201708, 0.00370995, 0.00782772, 0.014608, 0.0296672, 0.0543108, 0.119673, 0.269981, 0.702621, 1.92741}}
We compare these times with other methods.
Multinomial Method
as above:
RExp[n_] := Expand[y Plus[R[0], Total[y^# R[#] & /@ Range[n]]]]
RCalc[0, _] = 1;
RCalc[n_, m_] := With[{basis = Subtract[Tally[Join[Range[n + m], #]][[All, 2]],
Table[1, {n + m}]] & /@ Select[IntegerPartitions[n + m], Length[#] > m - 1 &][[2 ;; -1]]},
Total@ReplaceAll[ Times[-1/m, Multinomial @@ #, c[Total[#]],
Times @@ Power[RSet[# - 1] & /@ Range[n + m], #]] & /@ basis, {c[m] -> 1}]]
MultinomialExpand[n_, m_] := (Clear@RSet; Set[RSet[#], Expand@RCalc[#, m]] & /@ Range[0, n];
Expand[RExp[n] /. R[o_] :> RCalc[o, m]])
The code is a conceptually simple, straightforward realization of the solution method discussed for case
$m=2$ in Plane Pendulum and Beyond (rejected by American Journal of Physics), generalized to any
$m$. This method is easy to prove, especially for someone versed in ring theory. The algorithm takes advantage of a graded coefficient-algebra associated with partitions of the integer numbers. Rather than writing out a full proof, we can test equivalence:
SameQ[MultinomialExpand[10, #] & /@ Range[5], MmaExpand[10, #] & /@ Range[5]]
Out[]= True
And now we can run the timing statistics up to
$n=18$
t2 = Outer[AbsoluteTiming[MultinomialExpand[#2, #1]][[1]] &, Range[5], Range[18]]
Out[]={{0.000350166, 0.000335676, 0.0006466, 0.00102544, 0.00187701,
0.00335827, 0.0050605, 0.00829471, 0.0137534, 0.0213327, 0.0338478,
0.0526303, 0.0818673, 0.127584, 0.197492, 0.303197, 0.461779,
0.705808}, {0.00059166, 0.000385183, 0.000731424, 0.00141787,
0.00256708, 0.00438643, 0.0072424, 0.0121079, 0.0196304, 0.0317456,
0.0498247, 0.0797138, 0.123864, 0.19419, 0.297837, 0.463815,
0.703707, 1.08945}, {0.000783647, 0.000391522, 0.000853077,
0.00165484, 0.00296434, 0.00541067, 0.00877981, 0.0160512,
0.0248739, 0.0400204, 0.0637266, 0.101257, 0.158744, 0.247118,
0.392642, 0.600964, 0.915037, 1.42288}, {0.000755876, 0.000407823,
0.000880547, 0.00177226, 0.0032173, 0.00567963, 0.00968088, 0.01652,
0.0290402, 0.0468616, 0.0753077, 0.120092, 0.191354, 0.298932,
0.466456, 0.734795, 1.09722, 1.70526}, {0.000888697, 0.000464272,
0.000976541, 0.00196093, 0.00343374, 0.00653271, 0.0109065,
0.0190267, 0.0313326, 0.0523583, 0.0833902, 0.127929, 0.202708,
0.327367, 0.512287, 0.798683, 1.23594, 1.91088}}
Still we are under two seconds.
Magic Number Theory Method
as above:
SF[0, 0, m_] = 1;SF[n_, k_, m_] := SF[n, k, m] =
If[Or[k > n, k < 0], 0, If[And[n == 0, k == 0], 1,
SF[n - 1, k - 1, m] + (m*n - 1)*SF[n - 1, k, m]]]
GeneralPolys[n_, m_] := MapThread[ Dot, {Table[SF[i, j, m], {i, 0, n - 1}, {j, 0, i}],
Table[x^j, {i, 0, n - 1}, {j, 0, i}]}]
GeneralT[n_, m_] := With[{ps = GeneralPolys[n, m]},
Table[(-1)^j ps[[j]] /. {x -> i + 2}, {i, 1, n}, {j, 1, i}]]
Basis[n_, m_] := Total /@ Map[
Times[m^(-Length[#]) 1/Times @@ (Tally[#][[All, 2]]!),
Times @@ (# /. x_Integer :> c[x + m])] &,
Function[{a}, Select[IntegerPartitions[n], Length[#] == a &]] /@
Range[n], {2}]
MagicExpand[n_, m_] := Expand[y + Dot[MapThread[Dot, {GeneralT[n, m], Basis[#, m] & /@ Range[n]}],
y^Range[2, n + 1]]];
Exploring the expansion coefficients in the OEIS partition triangles A111785 and A276738, I conjectured that it would be possible to store only a regular triangle, i.e., row length equals row index. For example, see: A283247, and triangles for
$m=1,2,3...12$ are given in a previous post above. For the final formulation I used Peter Luschny's definitions for the Stirling-Frobenius Cycle numbers . It's conceivable that the above algorithm is easy for a pure mathematician to prove, and also that the above algorithm is already known to someone. I don't know. I found this method by a smart empirical investigation. At this time I can only say that it works, relative to other proven methods, to many orders of magnitude. Here we can check
$15$ quickly
SameQ[MagicExpand[15, #] & /@ Range[15], MultinomialExpand[15, #] & /@ Range[15]]
Out[72]= True
This is a promising result. Although I'm not trained as a mathematician, and mathematicians don't seem to like me very well lately, I'm interested to work on a proof starting from the known algorithm using multinomial coefficients. For now, let's just do the timing test, up to
$n=30$
t3 = Outer[AbsoluteTiming[MagicExpand[#2, #1]][[1]] &, Range[5], Range[30]]
Out[75]= {{0.000517401, 0.000730217, 0.00129441, 0.00241826,
0.00313761, 0.00480814, 0.00677571, 0.00235547, 0.00322757,
0.00458355, 0.00661482, 0.00910492, 0.0127276, 0.0178956, 0.0245657,
0.03328, 0.045086, 0.0608486, 0.0816343, 0.111034, 0.145875,
0.192592, 0.252839, 0.331296, 0.431803, 0.554355, 0.709992,
0.907644, 1.15345, 1.45812}, {0.000193195, 0.000157575, 0.000248437,
0.000478158, 0.000638147, 0.000984389, 0.00152262, 0.00219397,
0.00318681, 0.00455035, 0.00642736, 0.00907141, 0.0128466,
0.0179599, 0.0244666, 0.0334372, 0.0457468, 0.0618206, 0.0836055,
0.115272, 0.151878, 0.196921, 0.259114, 0.338644, 0.436268,
0.564819, 0.728962, 0.920223, 1.17813, 1.47938}, {0.000208892,
0.000162405, 0.000285868, 0.000402993, 0.000645996, 0.00100673,
0.00151145, 0.00223261, 0.00324719, 0.00460649, 0.00675066,
0.00924921, 0.0127491, 0.0177939, 0.0250812, 0.0334789, 0.0458992,
0.0638416, 0.0865447, 0.112189, 0.149649, 0.198407, 0.25906,
0.34008, 0.436906, 0.56552, 0.727684, 0.928567, 1.18617,
1.52182}, {0.000167536, 0.000164216, 0.000273794, 0.000405408,
0.000670145, 0.000981371, 0.00175083, 0.00223442, 0.00321972,
0.00472271, 0.00701268, 0.0105626, 0.0139251, 0.0198001, 0.0275424,
0.0371674, 0.0510624, 0.0657576, 0.0853008, 0.120408, 0.156297,
0.213033, 0.280924, 0.365606, 0.467034, 0.589213, 0.780763, 1.02078,
1.23597, 1.59574}, {0.000196817, 0.000165725, 0.000252361,
0.000439821, 0.000629393, 0.000999784, 0.00157846, 0.0022308,
0.00322183, 0.00483742, 0.00662297, 0.00945479, 0.0128339,
0.0181477, 0.0254782, 0.034367, 0.0472682, 0.0632687, 0.0855504,
0.113633, 0.152079, 0.201328, 0.268378, 0.346395, 0.478177,
0.617492, 0.742203, 0.935041, 1.20908, 1.52182}}
again, under two seconds max time.
Graphing Time Results
Show[
ListLinePlot[t1, PlotStyle -> (Blend[{Red, Orange}, #/5] & /@ Range[5]),
PlotRange -> All], ListLinePlot[t2, PlotStyle -> (Blend[{Blue, Green}, #/5] & /@ Range[5]),
PlotRange -> All], ListLinePlot[t3, PlotStyle -> Purple, PlotRange -> All],
PlotRange -> All, AxesLabel -> {Style["n", 20], Style["t(s)", 20]}, ImageSize -> 800 ]
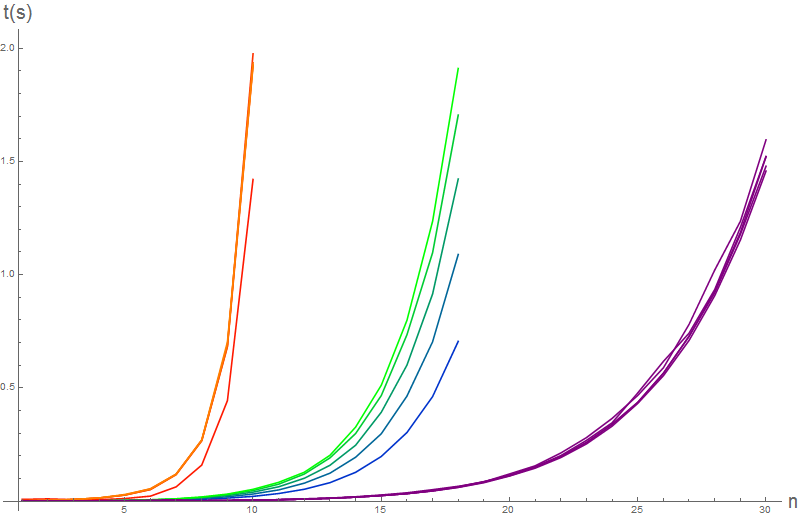
This is the same graph as above, but with extra explanation, maybe it is easier to interpret. As predicted, variation with
$m$ is insignificant compared to the blow up with
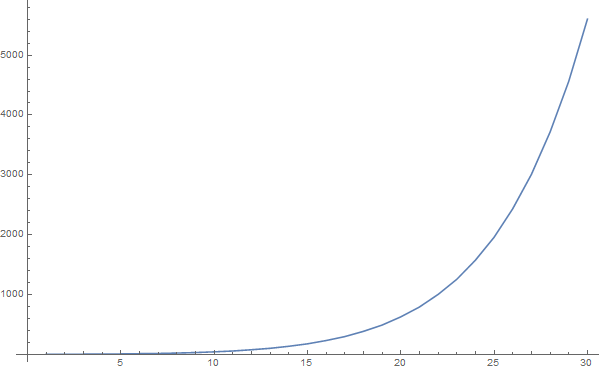
$n$, associated with partition complexity class. Compare with a plot of the partition numbers:
ListLinePlot[Length@IntegerPartitions[#] & /@ Range[20], ImageSize -> 800]
The time graph also shows that in the partition complexity class, regardless of
$m$, the magic method vastly outperforms other methods. The easy multinomial method only outperforms the method using built-in inverse function. Setting a time limit of
$2s$, we can only compute approximately
$10$,
$18$,
$30$ orders of magnitude, as indexed by
$n$.
Again, the most interesting feature of the graph is the stability of the magic method with regard to variation of
$m$. If you look closely at the code, tasks seperate into an
$\mathcal{O}(n^2)$ listing of coefficients, and an
$\mathcal{O}(p(n))$ expansion of functions
$g_{i,j}(\mathbf{c})$, called a "basis". Again, if the basis function can be optimized by recursive programming, then the timing can be further reduced.
Danny, does this make more sense? If not maybe we can get a third opinion? Seems like Michael Trott would probably also have some idea about this sort of calculation. Ultimately it would also be interesting to hear from one of you inside the company: How does the Mma algorithm work for inverting a series with symbolic coefficients?
That's all for now,
Brad