Large amounts of data become evermore available - often these datasets are very valuable and difficult to access. In this post I will show how to use air traffic data to generate visualisations like this one.

On the website http://www.flightradar24.com one can find live flight information of most of the civil air traffic. A great amount of information on all current flights is being made available, such as position and altitude, call sign, type of plane, origin and destination and many more. There are different subscription plans with different features. The largest business plan even allows you to commercially use the data or use them for public display. Alternatively, you can contribute data https://www.flightradar24.com/add-coverage. This can be done with a tiny RTL-SDR receiver, such as this one. The setup is quite straight forward; I am usually working on Macs on which I had trouble making this work. On a Windows machine (which I only got for this purpose), the setup is quick. The software for sharing your data can be downloaded from flightradar24's website. You will also need a driver for the SDR stick, which you can download from here. You should make sure that you have a good visibility of the sky and that the computer and internet connection are stable. I had to use a Windows 8/Windows 10 machine. It was quite annoying that the machine routinely reboots for software updates. If you want uninterrupted monitoring you will have to deactivate this feature. I have no experience with Windows so this was more complicated than I expected. I found a nice set of instructions here.
Once all of this is done and you donate your data, you will automatically upgraded to the Business plan and will have access to a very rich dataset. You will, for example, be allowed to download up to 1000 csv files per month with detailed tracking information of flights in the database. There is much more data available and using the Wolfram Language to analyse it seems to be quite natural.
First explorations
I download data for a flight from Frankfurt to Aberdeen in csv format. Each row contains a time stamp, date and time of the entry, the callsign, the position (as a string), altitude, speed and direction. I can import the data and then plot it:
flightdata = Import["/Users/thiel/Desktop/Flight_LH971_(cb294d1).csv"];
GeoGraphics[{Red, Thick, GeoPath@(ToExpression[#] & /@ Flatten[StringSplit[#, ","] & /@ flightdata[[2 ;;, {4}]], 1])}]
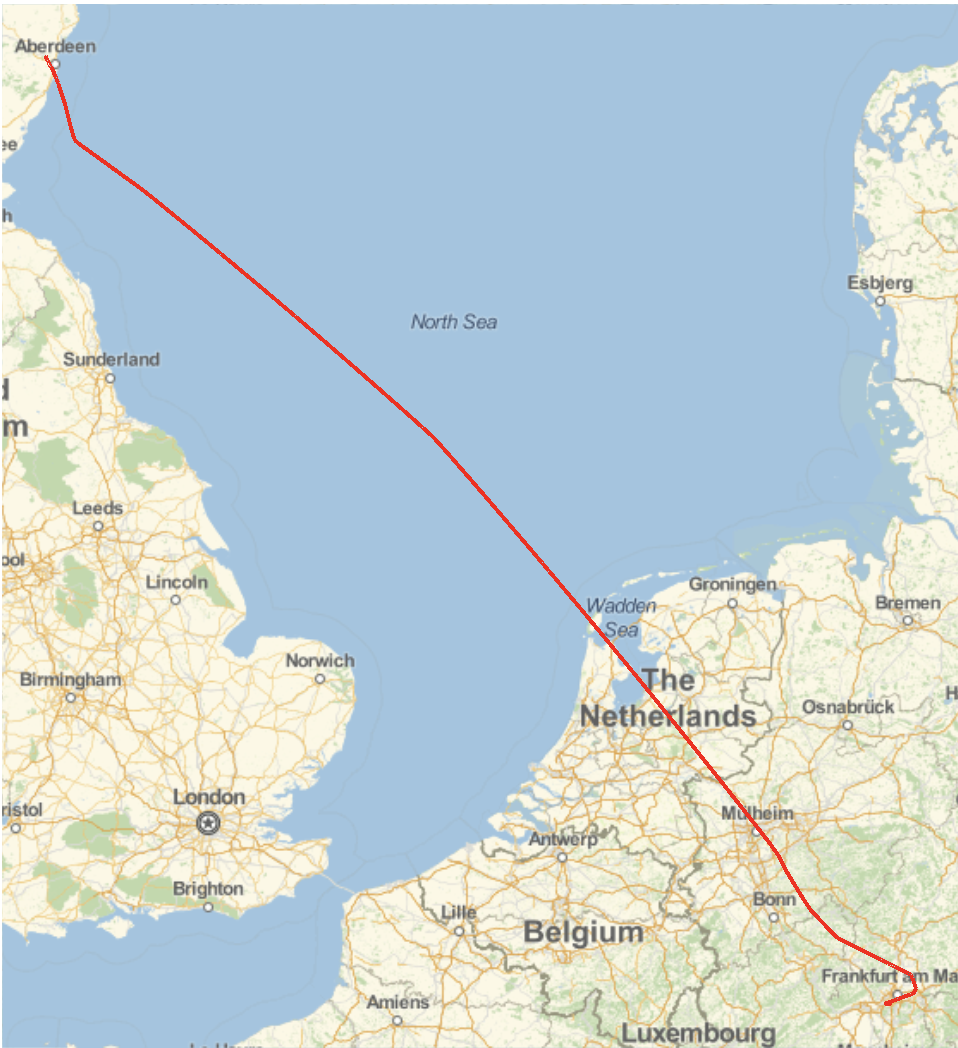
I needed to use StringSplit, because the GPS coordinates come in the form of a single string. Next, I can plot the path in 3D. I can clean the data to get it into the right format:
flightphs = {Join[ToExpression[StringSplit[#[[1]], ","]], {ToExpression[#[[2]]]}],ToExpression[#[[3]]]} & /@ flightdata[[2 ;;, {4, 5, 6}]];
Graphics3D[{Red, Thick, Line[{#[[1]], #[[2]], #[[3]]/30000.} & /@ flightphs[[All, 1]]]}]
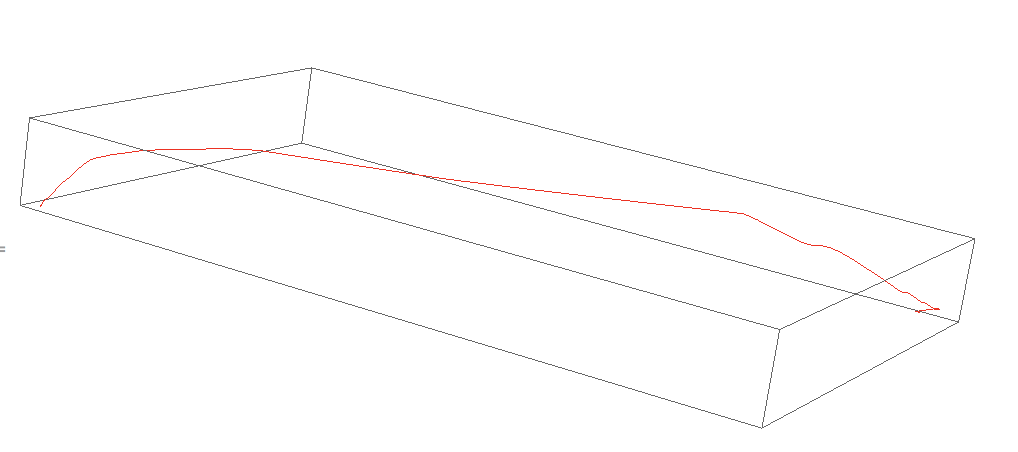
The 30000 that I use to divide the altitude is just a scaling factor. (Note that the altitude value comes in feet.) We can now join the flight path to one of Mathematica's maps:
Show[Graphics3D[{Red, Thick, Line[{#[[1]], #[[2]], -#[[3]]/30000.} & /@ flightphs[[All, 1]]]},
Lighting -> {{"Ambient", White}}],
Graphics3D[{Texture[Image[GeoGraphics[GeoPath[GeoPosition[flightphs[[All, 1]]]]]]],
Polygon[(PadRight[#, 3] & /@ Tuples[GeoBounds[GeoPath@GeoPosition[flightphs[[All, 1]]], Scaled[0.05]]])[[{1, 2, 4, 3}]],
VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}], ImageSize -> Full]
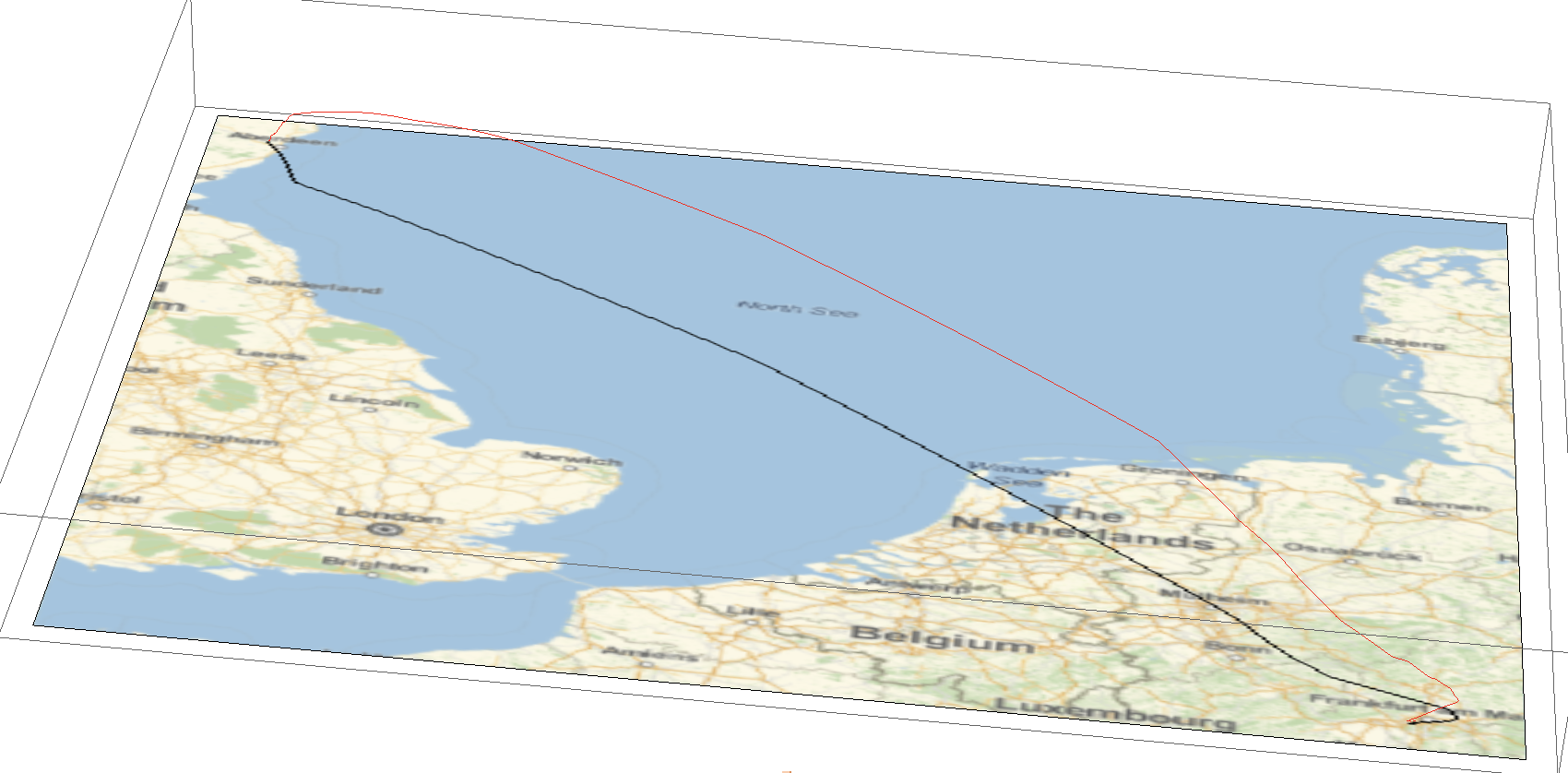
It also looks nice on a satellite image background:
Show[Graphics3D[{Red, Thickness[0.005], Line[{#[[1]], #[[2]], -#[[3]]/30000.} & /@ flightphs[[All, 1]]]},
Lighting -> {{"Ambient", White}}], Graphics3D[{Texture[Image[GeoGraphics[{Opacity[0],
GeoPath[GeoPosition[flightphs[[All, 1]]]]}, GeoBackground -> "Satellite"]]],
Polygon[(PadRight[#, 3] & /@ Tuples[GeoBounds[GeoPath@GeoPosition[flightphs[[All, 1]]],
Scaled[0.05]]])[[{1, 2, 4, 3}]], VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}], ImageSize -> Full]
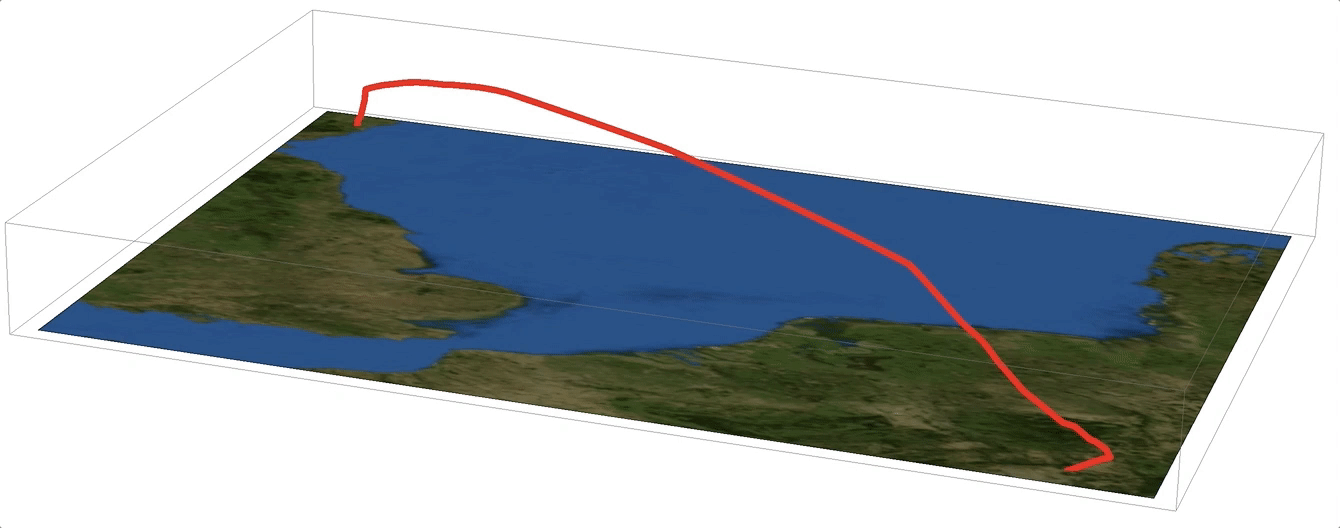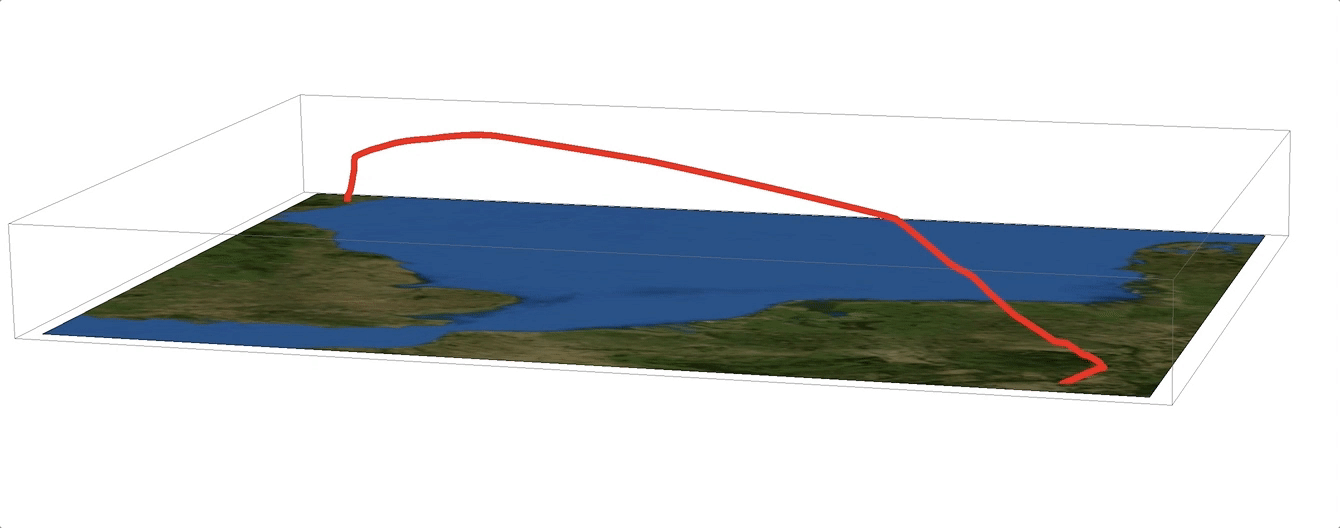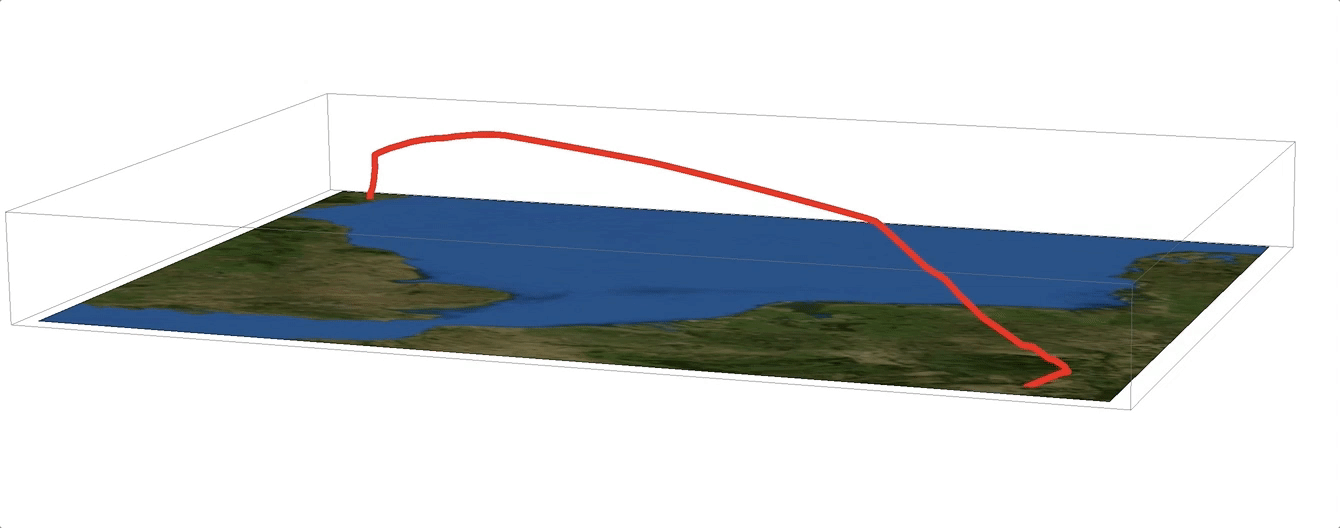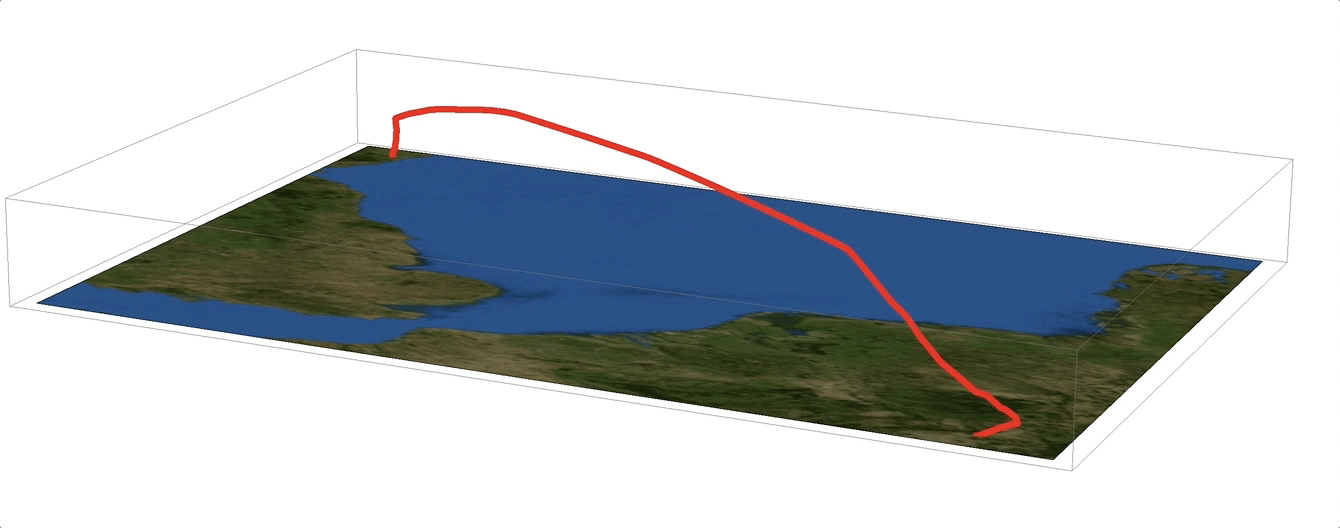
Multiple flights
Next, I download 10 trajectories of the flight LH971 from Frankfurt to Aberdeen.
FileNames["*", "/Users/thiel/Desktop/Aberdeen LH971/"]

I then import all of the trajectories:
flightdataall = Import /@ FileNames["*", "/Users/thiel/Desktop/Aberdeen LH971/"];
This corresponds to 282 entries - each consisting of time stamp, date and time of the entry, the callsign, the position (as a string), altitude, speed and direction. I can clean them all up
flightphsall = ({Join[ToExpression[StringSplit[#[[1]], ","]], {ToExpression[#[[2]]]}], ToExpression[#[[3]]]} & /@ #[[2 ;;, {4, 5, 6}]] &) /@ flightdataall;
and then plot them together:
Show[Graphics3D[{Red, Thickness[0.004],
Line[{#[[1]], #[[2]], -#[[3]]/30000.} & /@ #[[All, 1]] & /@ flightphsall]}, Lighting -> {{"Ambient", White}},
ViewPoint -> {-10.`, 5.`, -5.`}, ViewVertical -> {0.8924410944866072`, -0.23945064940819427`, -7.766116131708949`}],
Graphics3D[{Texture[Image[GeoGraphics[{Opacity[0], GeoPath[GeoPosition[flightphs[[All, 1]]]]},
GeoBackground -> "Satellite", GeoRange -> {{Min[#[[All, 1, 1]]], Max[#[[All, 1, 2]]]}, {Min[#[[All, 2, 1]]], Max[#[[All, 2, 2]]]}} & @(GeoBounds[GeoPath@GeoPosition[#[[All, 1]]], Scaled[0.05]] & /@ flightphsall)]]],
Polygon[(PadRight[#, 3] & /@ Tuples[{{Min[#[[All, 1, 1]]], Max[#[[All, 1, 2]]]}, {Min[#[[All, 2, 1]]], Max[#[[All, 2, 2]]]}} & @(GeoBounds[
GeoPath@GeoPosition[#[[All, 1]]], Scaled[0.05]] & /@ flightphsall)])[[{1, 2, 4, 3}]], VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}],
ImageSize -> Full]

Note that I use ViewPoint and ViewVertical options. This is because without them, the orientation of the resulting 3D graphic is not optimal. So I plotted the image without the additional options and then rotated it until I was happy with the orientation. Then I use the function
extractViewPos[img_] := Flatten[Union[Extract[img, Position[img, #]] & /@ {ViewPoint -> _, ViewCenter -> _, ViewVertical -> _, ViewAngle -> _,ViewVector -> _, ViewRange -> _}]];
Just copy the image into the square brackets and execute:
extractViewPos[-Graphic goes here-]
and get
{ViewPoint -> {-10., 5., -5.}, ViewVertical -> {0.892441, -0.239451, -7.76612}}
This is not my function, but I found it online and have been using it ever since.
Animating a flight
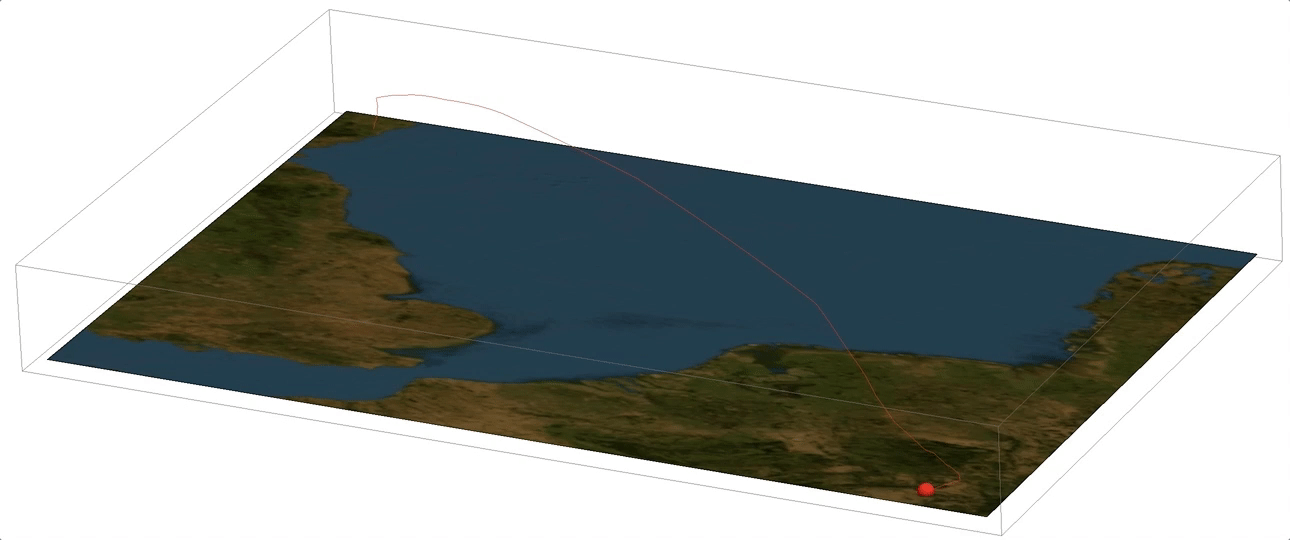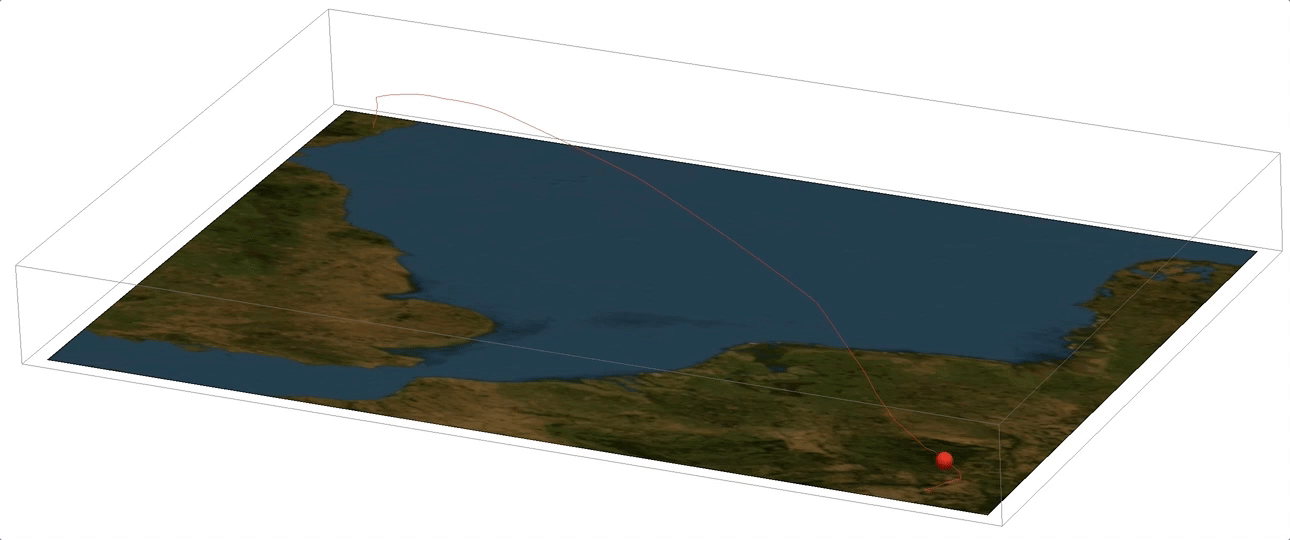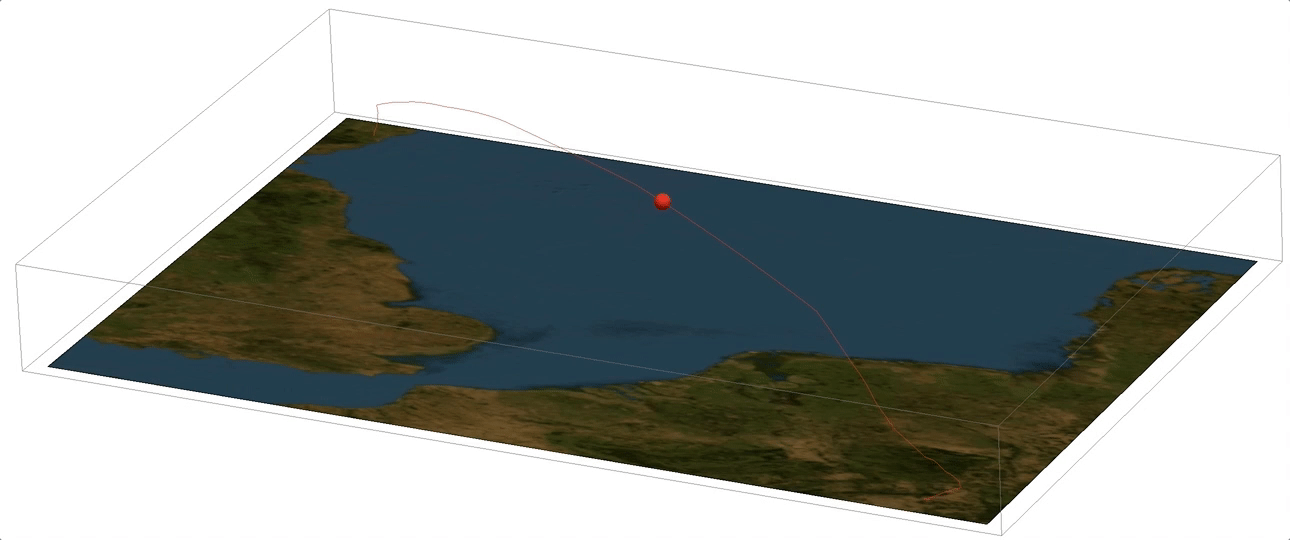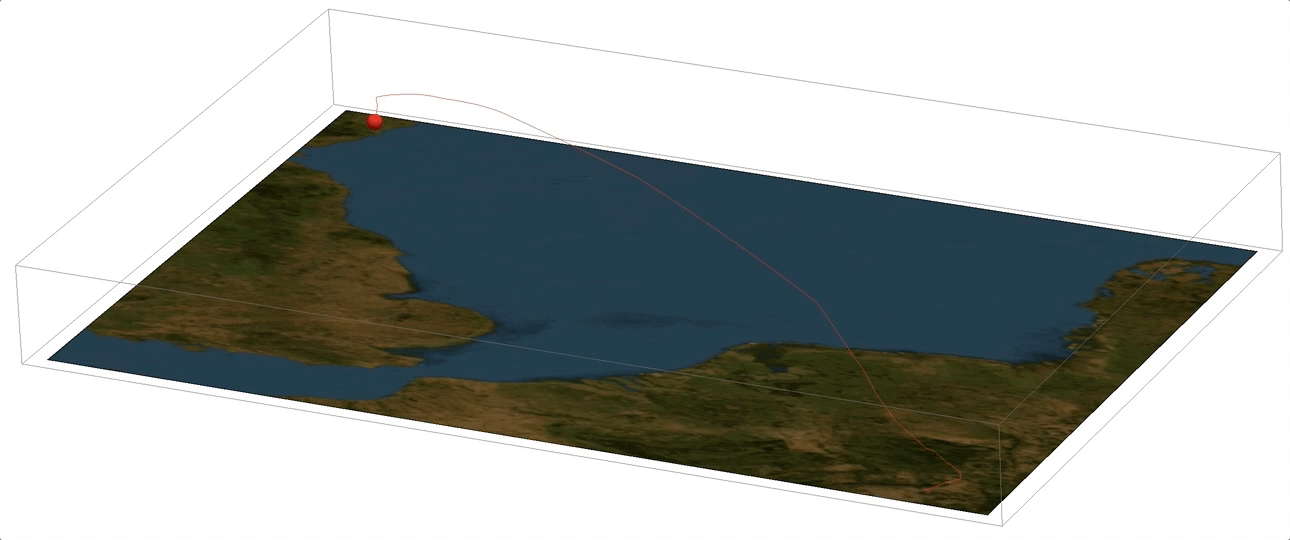
Now we can mark the position of the aeroplane by a sphere and animate the flight:
backround3D2 =
Show[Graphics3D[{Red, Thick, Line[{#[[1]], #[[2]], -#[[3]]/30000.} & /@ flightphs[[All, 1]]]},Lighting -> {{"Ambient", White}},
ViewPoint -> {-10.`, 5.`, -5.`}, ViewVertical -> {0.8924410944866072`, -0.23945064940819427`, -7.766116131708949`}],
Graphics3D[{Texture[Image[GeoGraphics[{Opacity[0], GeoPath[GeoPosition[flightphs[[All, 1]]]]}, GeoBackground -> "Satellite"]]],
Polygon[(PadRight[#, 3] & /@ Tuples[GeoBounds[GeoPath@GeoPosition[flightphs[[All, 1]]], Scaled[0.05]]])[[{1, 2, 4, 3}]],
VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}],ImageSize -> Full];
Manipulate[
Show[Graphics3D[{Red, Sphere[{#[[1]], #[[2]], -#[[3]]/30000.} & @flightphs[[k, 1]], 0.1]}, ViewPoint -> {-10.`, 5.`, -5.`},
ViewVertical -> {0.8924410944866072`, -0.23945064940819427`, -7.766116131708949`}, ImageSize -> Full], backround3D2], {k, 1, Length[flightphs],5}]
The multiple flights I have displayed above are the same route but executed by different aeroplanes. Later we will follow individual aeroplanes. But first we will look at the peculiar take-off and landing patterns.
Take-off and landing patterns
When we look at the take-off and touch-down times we observe that there are two main directions for both starting and destination airports. What decides which direction the planes are taking?
Graphics3D[{Red, Thickness[0.004],
Line[{#[[1]], #[[2]], -#[[3]]/30000.} & /@ #[[All, 1]] & /@ flightphsall]}, Lighting -> {{"Ambient", White}},
ViewPoint -> {-10.`, 5.`, -5.`}, ViewVertical -> {0.8924410944866072`, -0.23945064940819427`, -7.766116131708949`}]
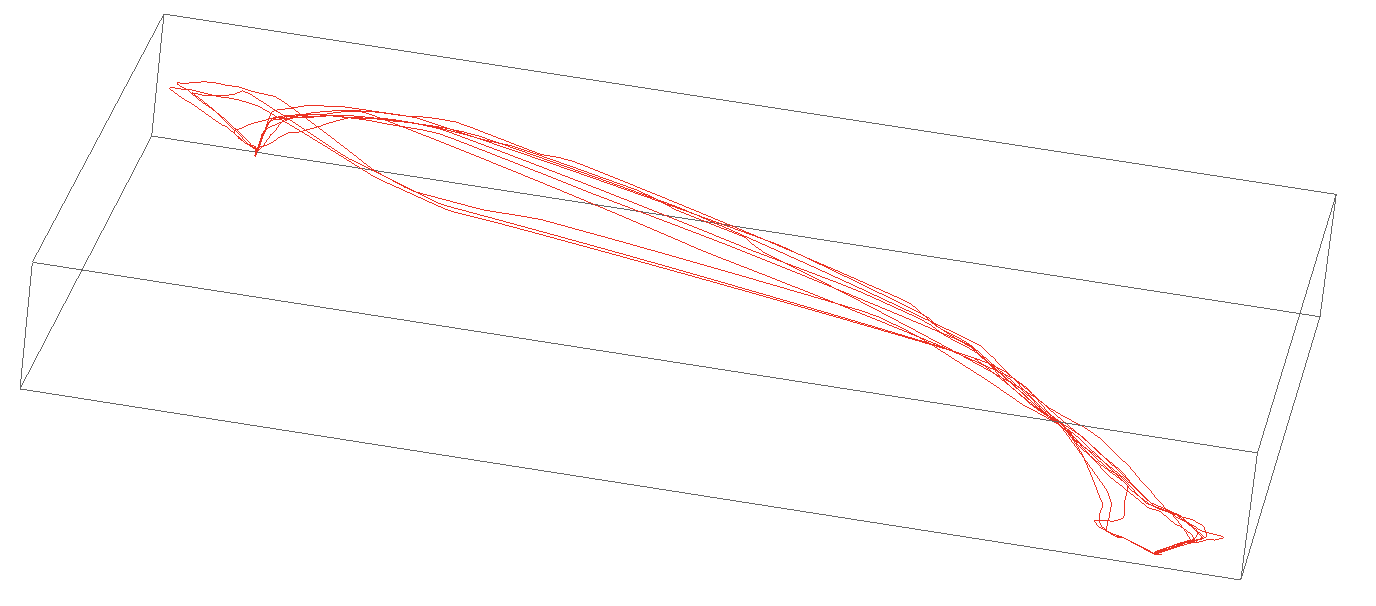
We first need to determine the wind direction in Frankfurt and Aberdeen on days with either of the two take-off/landing directions. First for Frankfurt.
frankfurttimeheading = Table[Select[flightdataall[[k]], #[[5]] > 4000 &][[1, {1, -1}]], {k, 1, 10}]
which gives
{{1488564623, 69}, {1488650932, 250}, {1488737193, 250}, {1488823517, 249}, {1488909842, 250}, {1488996665, 249}, {1489080927, 250}, {1489168646, 250}, {1489254863, 69}, {1489341257, 69}}
We see that there are two clusters, one at around 69 degrees and one at around 250 degrees:
fdates69 = FromUnixTime /@ Select[frankfurttimeheading, #[[2]] < 100 &][[All, 1]];
fdates250 = FromUnixTime /@ Select[frankfurttimeheading, #[[2]] > 100 &][[All, 1]];
The Wolfram Language knows the wind directions for those days:
WindDirectionData[Entity["Airport", "EDDF"], fdates69]
(*{Quantity[60., "AngularDegrees"], Quantity[70., "AngularDegrees"], Quantity[70., "AngularDegrees"]}*)
and
WindDirectionData[Entity["Airport", "EDDF"], fdates250]
{Quantity[250., "AngularDegrees"], Quantity[170., "AngularDegrees"], Quantity[-60., "AngularDegrees"], Quantity[210., "AngularDegrees"],
Quantity[200., "AngularDegrees"], Quantity[-70., "AngularDegrees"], Quantity[70., "AngularDegrees"]}
It knows the wind vector data; here we plot it for the two situations.
Graphics[Arrow[{{0, 0}, #}] & /@ QuantityMagnitude[WindVectorData[Entity["Airport", "EDDF"], fdates250]]]
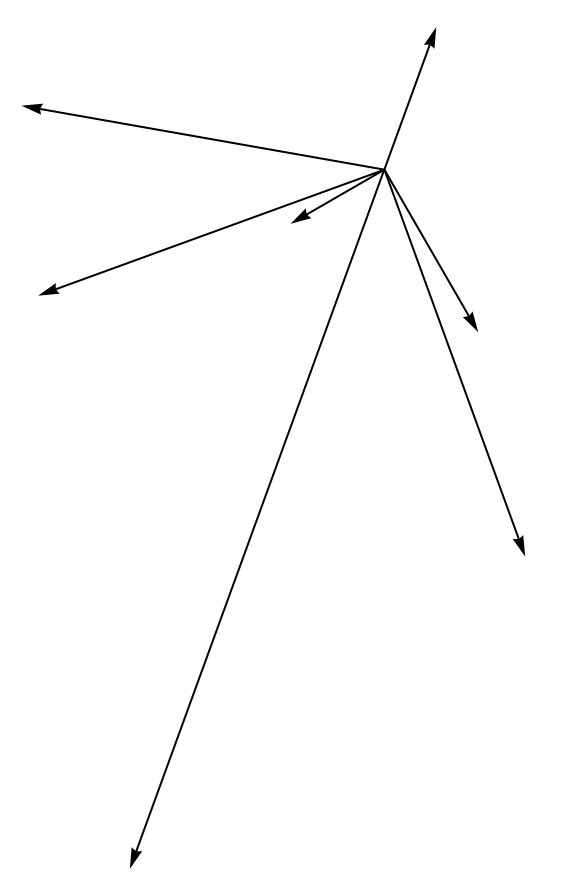
Graphics[Arrow[{{0, 0}, #}] & /@ QuantityMagnitude[WindVectorData[Entity["Airport", "EDDF"], fdates69]]]
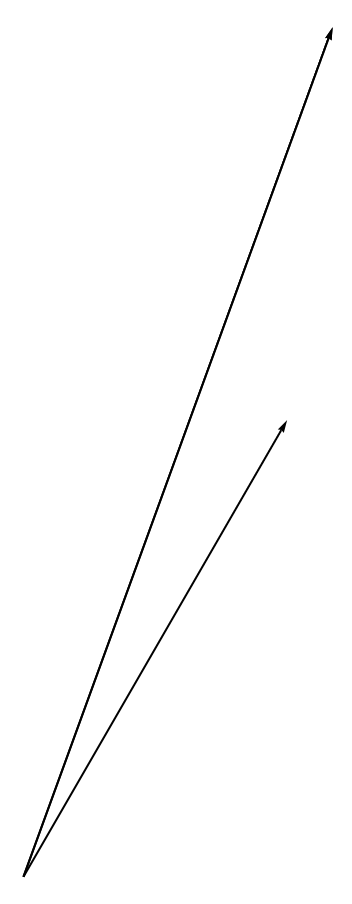
If we now average the data
Show[Graphics[{Red, Thick, Arrow[{{0, 0}, Mean[QuantityMagnitude[WindVectorData[Entity["Airport", "EDDF"], fdates250]]]}]}],
Graphics[{Green, Thick, Arrow[{{0, 0}, Mean[QuantityMagnitude[WindVectorData[Entity["Airport", "EDDF"], fdates69]]]}]}]]

We see that the wind direction seems to correlate with the take off direction at least for relatively strong winds. This is in agreement with general advice of how to choose the runway. We can now do the same for Aberdeen.
aberdeentimeheading = Table[Select[Reverse[flightdataall[[k]]], #[[5]] > 4000 &][[1, {1, -1}]], {k, 1, 10}];
We split the dates into two groups: smaller and larger than 200 degrees.
adates230 = FromUnixTime /@ Select[frankfurttimeheading, #[[2]] > 200 &][[All, 1]];
adates169 = FromUnixTime /@ Select[frankfurttimeheading, #[[2]] < 200 &][[All, 1]];
These are the respective vectors:
Graphics[Arrow[{{0, 0}, #}] & /@ QuantityMagnitude[WindVectorData[Entity["City", {"Dundee", "DundeeCity", "UnitedKingdom"}], adates169]]]
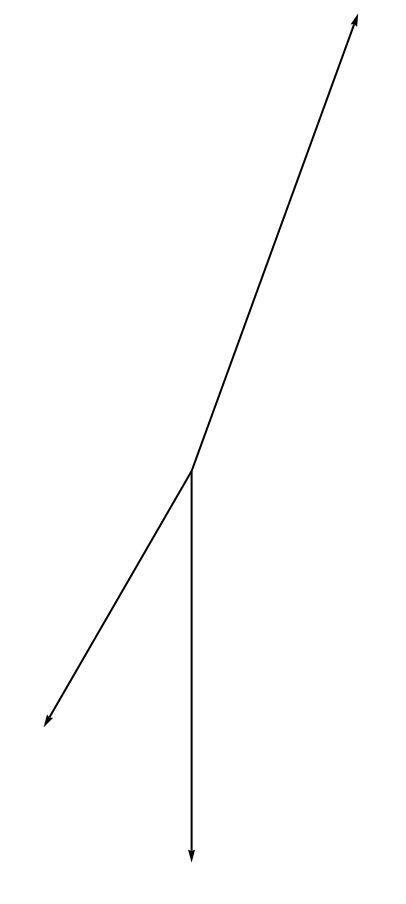
Graphics[Arrow[{{0, 0}, #}] & /@ QuantityMagnitude[WindVectorData[Entity["City", {"Dundee", "DundeeCity", "UnitedKingdom"}], adates230]]]
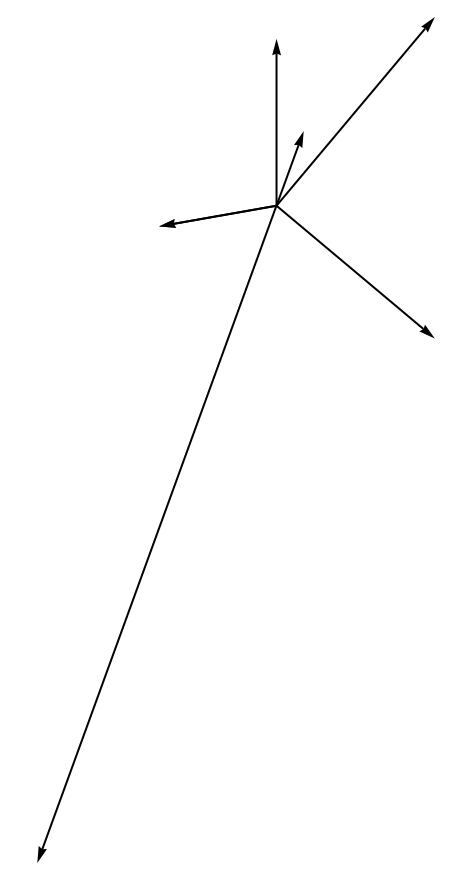
Now we can plot this for the different averaged directions.
Show[Graphics[{Red, Thick, Arrow[{{0, 0}, -Mean[QuantityMagnitude[WindVectorData[Entity["City", {"Dundee", "DundeeCity", "UnitedKingdom"}],adates169]]]}]}],
Graphics[{Green, Thick, Arrow[{{0, 0}, -Mean[QuantityMagnitude[WindVectorData[Entity["City", {"Dundee", "DundeeCity", "UnitedKingdom"}],adates230]]]}]}]]
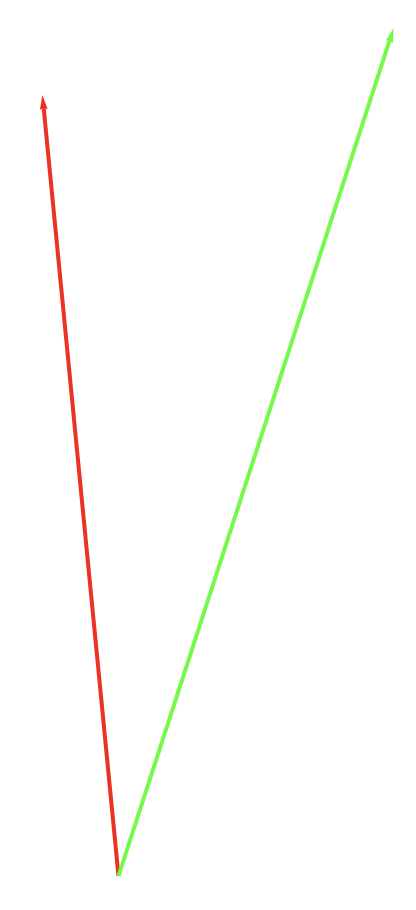
The pattern here is not so clear. This could be because of low wind speeds.
Following individual aeroplanes (short haul)
We can also follow an individual aeroplane (D-EACB) for, say, one month or so. Download the data and check that they are there:
FileNames["*", "/Users/thiel/Desktop/D-EACB/"]
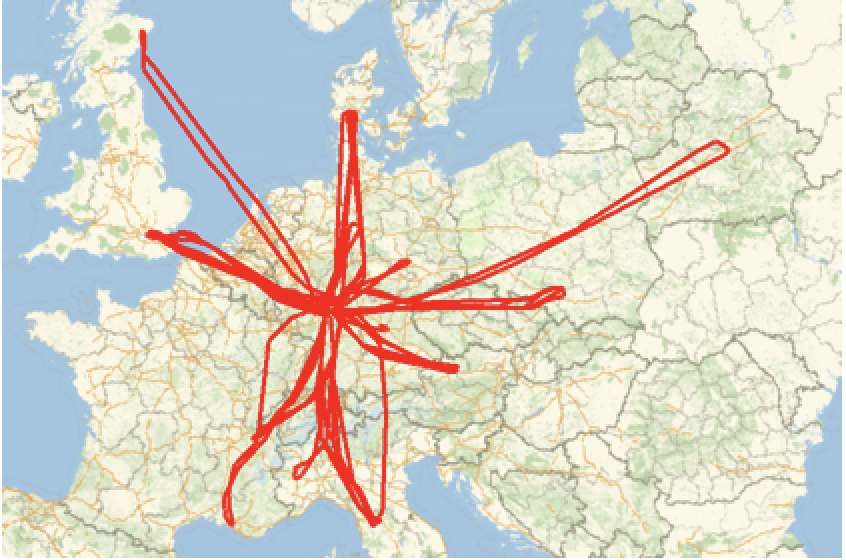
Import the data and plot everything:
flightdataDEACB = Import /@ FileNames["*", "/Users/thiel/Desktop/D-EACB/"];
GeoGraphics[{Red, Thick, GeoPath@(ToExpression[#] & /@ Flatten[StringSplit[#, ","] & /@ #, 1]) & /@
flightdataDEACB[[All, 2 ;;]][[All, All, {4}]]}]
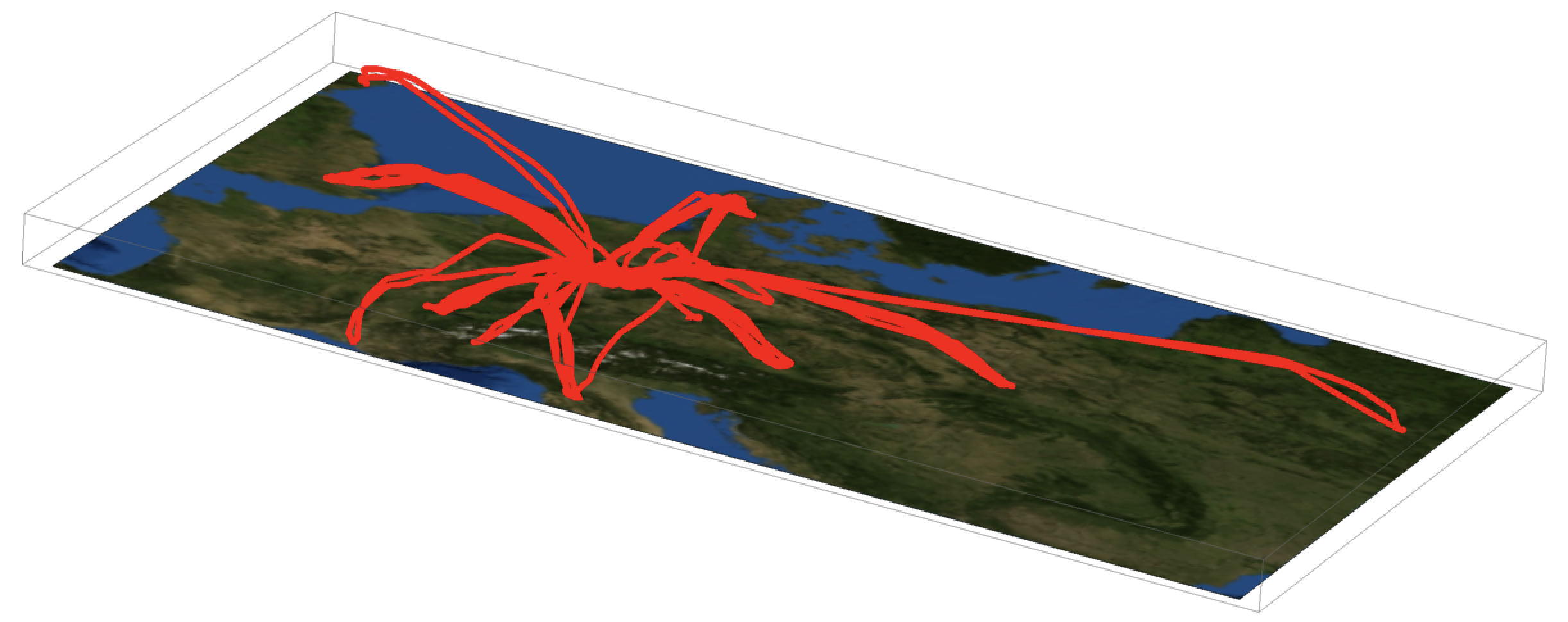
Of course, the same thing in 3D looks somewhat more impressive:
flightphsDEACB = ({Join[
ToExpression[
StringSplit[#[[1]], ","]], {ToExpression[#[[2]]]}],
ToExpression[#[[3]]]} & /@ #[[2 ;;, {4, 5, 6}]] &) /@
flightdataDEACB;
Show[Graphics3D[{Red, Thickness[0.004],
Line[{#[[1]], #[[2]], -#[[3]]/30000.} & /@ #[[All, 1]] & /@
flightphsDEACB]}, Lighting -> {{"Ambient", White}},
ViewPoint -> {-10.`, 5.`, -5.`},
ViewVertical -> {0.8924410944866072`, -0.23945064940819427`, \
-7.766116131708949`}],
Graphics3D[{Texture[
Image[GeoGraphics[{Opacity[0],
GeoPath@(ToExpression[#] & /@
Flatten[StringSplit[#, ","] & /@
flightdataDEACBjoin[[All, {4}]], 1])},
GeoBackground -> "Satellite",
GeoRange -> {{Min[#[[All, 1, 1]]],
Max[#[[All, 1, 2]]]}, {Min[#[[All, 2, 1]]],
Max[#[[All, 2, 2]]]}} & @(GeoBounds[
GeoPath@GeoPosition[#[[All, 1]]], Scaled[0.05]] & /@
flightphsDEACB), GeoProjection -> "Equirectangular"]]],
Polygon[(PadRight[#, 3] & /@
Tuples[{{Min[#[[All, 1, 1]]],
Max[#[[All, 1, 2]]]}, {Min[#[[All, 2, 1]]],
Max[#[[All, 2, 2]]]}} & @(GeoBounds[
GeoPath@GeoPosition[#[[All, 1]]], Scaled[0.05]] & /@
flightphsDEACB)])[[{1, 2, 4, 3}]],
VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}],
ImageSize -> Full]
Following individual aeroplanes (long haul)
All these flights are relatively short distance. I next choose a airbus A380 and look at its movements over a month or so.
flightdataGXLED = Import /@ FileNames["*", "/Users/thiel/Desktop/G-XLED/"];
GeoGraphics[{Red, Thick, GeoPath@(ToExpression[#] & /@ Flatten[StringSplit[#, ","] & /@ #, 1]) & /@
flightdataGXLED[[All, 2 ;;]][[All, All, {4}]]}, ImageSize -> Full]
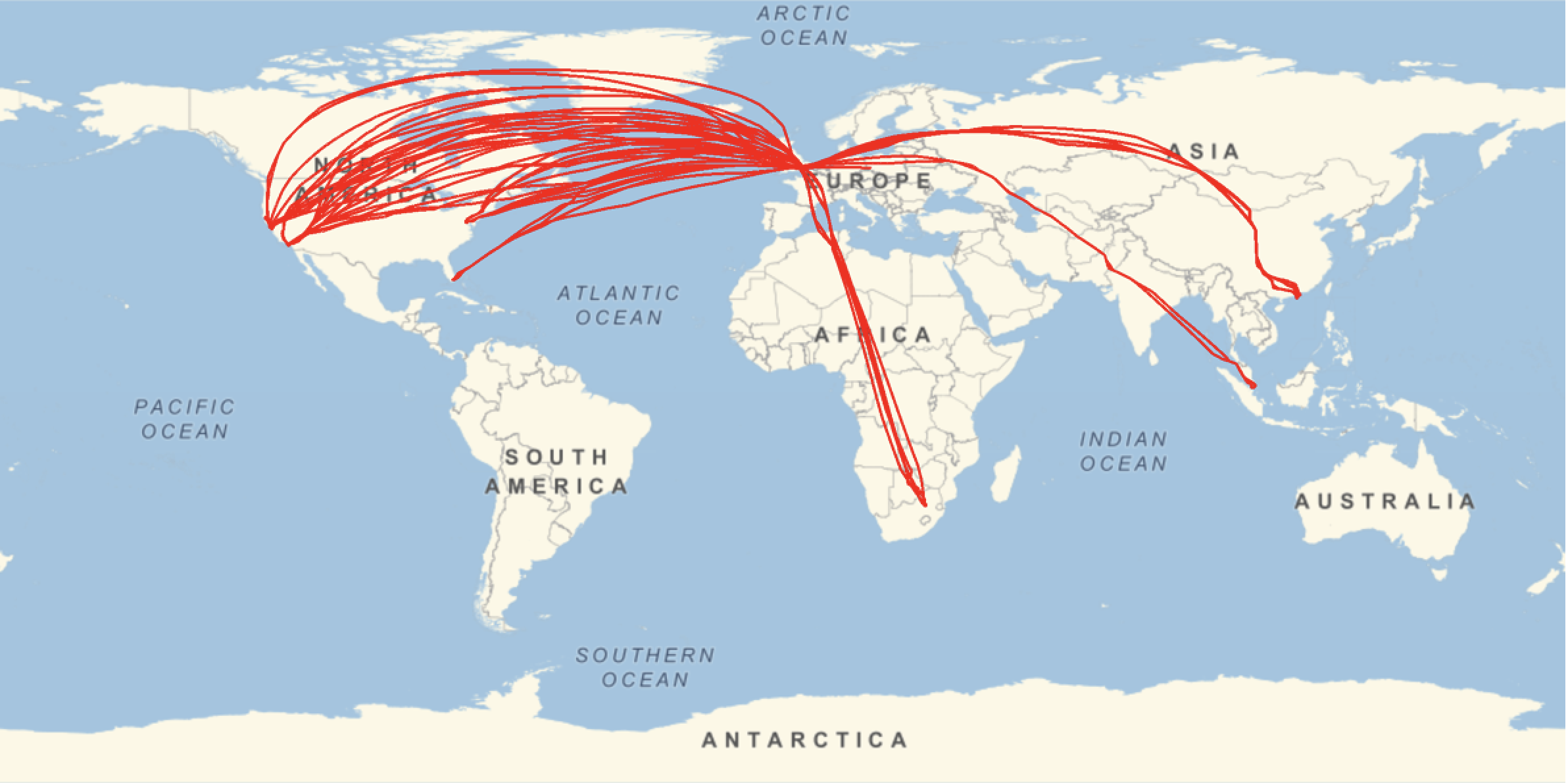
Again a 3D representation makes the flight paths come out much better. First we prepare the data:
flightdataGXLEDjoin = Flatten[Select[flightdataGXLED[[All, 2 ;;]], Head[#] > 0 &], 1];
flightphsGXLED = Select[({Join[ToExpression[StringSplit[#[[1]], ","]], {ToExpression[#[[2]]]}], ToExpression[#[[3]]]} & /@ #[[2 ;;, {4, 5, 6}]] &) /@
flightdataGXLED, Length[#] > 0 &];
Then we plot:
Show[Graphics3D[{Red, Thickness[0.002], Line[{#[[1]], #[[2]], -#[[3]]/3000.} & /@ #[[All, 1]] & /@ flightphsGXLED]}, Lighting -> {{"Ambient", White}},
ViewPoint -> {-10.67632349817987`, 3.7276615038423772`, -4.664042818603161`}, ViewVertical -> {0.11539873519013898`, -0.022518333742098193`, -0.9930639740530294`}, ImagePadding -> None],
Graphics3D[{Texture[Image[GeoGraphics[{Opacity[0], GeoPath@(ToExpression[#] & /@
Flatten[StringSplit[#, ","] & /@ flightdataGXLEDjoin[[All, {4}]], 1])}, GeoBackground -> "Satellite", GeoRange -> {{Min[#[[All, 1, 1]]],
Max[#[[All, 1, 2]]]}, {Min[#[[All, 2, 1]]], Max[#[[All, 2, 2]]]}} & @(GeoBounds[GeoPath@GeoPosition[#[[All, 1]]], Scaled[0.05]] & /@
flightphsGXLED), GeoProjection -> "Equirectangular", ImagePadding -> None]]], Polygon[(PadRight[#, 3] & /@
Tuples[{{Min[#[[All, 1, 1]]], Max[#[[All, 1, 2]]]}, {Min[#[[All, 2, 1]]], Max[#[[All, 2, 2]]]}} & @(GeoBounds[GeoPath@GeoPosition[#[[All, 1]]], Scaled[0.05]] & /@ flightphsGXLED)])[[{1, 2, 4, 3}]], VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}], ImageSize -> Full, ImagePadding -> None]
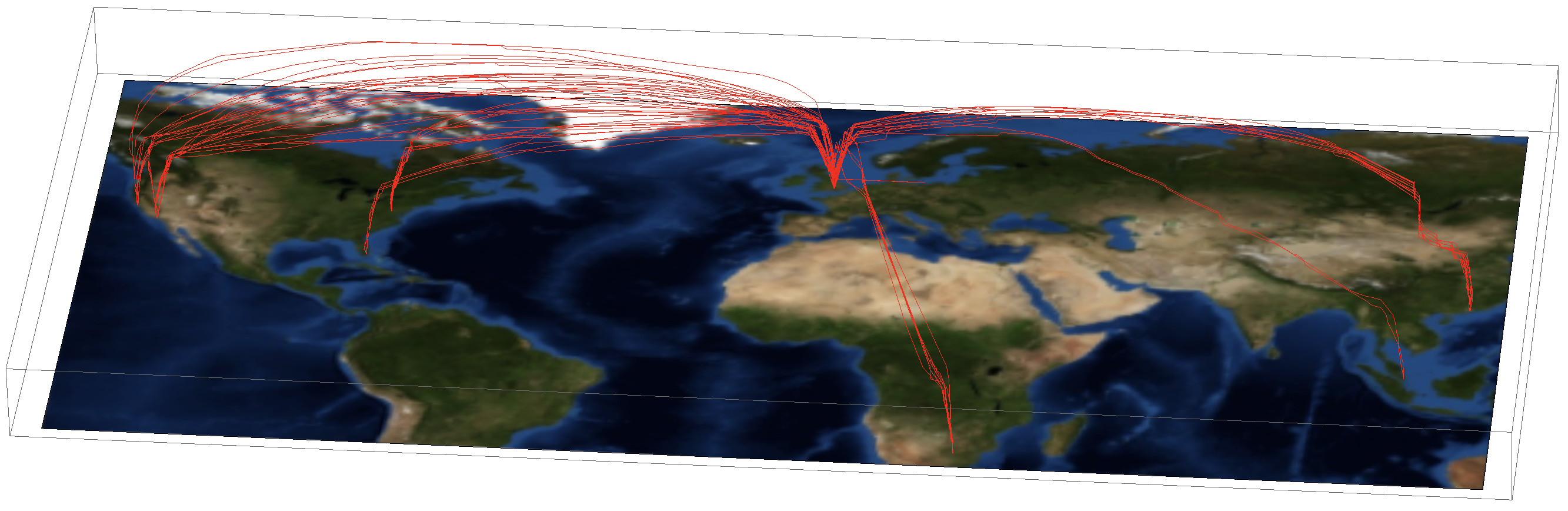
Representing the flight paths on a sphere
Note that I had to use the Equirectangular projection. Of course, particularly when looking at these long distances it would be more appropriate to represent the Earth as a sphere. We need to convert the coordinates and rescale the altitudes.
toCoordinates[coords_] := FromSphericalCoordinates[{#[[1]], Pi/2 - #[[2]], Mod[Pi + #[[3]], 2 Pi, -Pi]}] & /@ (Flatten[{1., #/360*2 Pi}] & /@ coords)
lengths[inputdata_] := 2.*(inputdata/Max[inputdata])
The representation of the path is somewhat related to another representation I posted on this community.
myFlightPath[data_, radius_, scale_] :=
Show[SphericalPlot3D[radius, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, TextureCoordinateFunction -> ({#5, 1 - #4} &),
PlotStyle -> Directive[Specularity[White, 10], Texture[Import["~/Desktop/backgroundimage.gif"]]],
Lighting -> "Neutral", Axes -> False, RotationAction -> "Clip", Boxed -> False, PlotPoints -> 100,
PlotRange -> {{-3, 3}, {-3, 3}, {-3, 3}}, ImageSize -> Full], Graphics3D[Flatten[{Green, Thickness[0.004],
Line[(radius + #[[2]]*scale)*#[[1]] & /@ Transpose[{toCoordinates[#[[All, 1]]], lengths[#[[All, 2]]]} &@({#[[1]], 1. #[[2]]} & /@ data)]]}]]]
Let's use that to plot one trajectory.
flightpath = {ToExpression[StringSplit[#[[4]], ","]], #[[6]]} & /@ flightdataGXLED[[2, 2 ;;]];
myFlightPath[flightpath, 2, 1/3.]
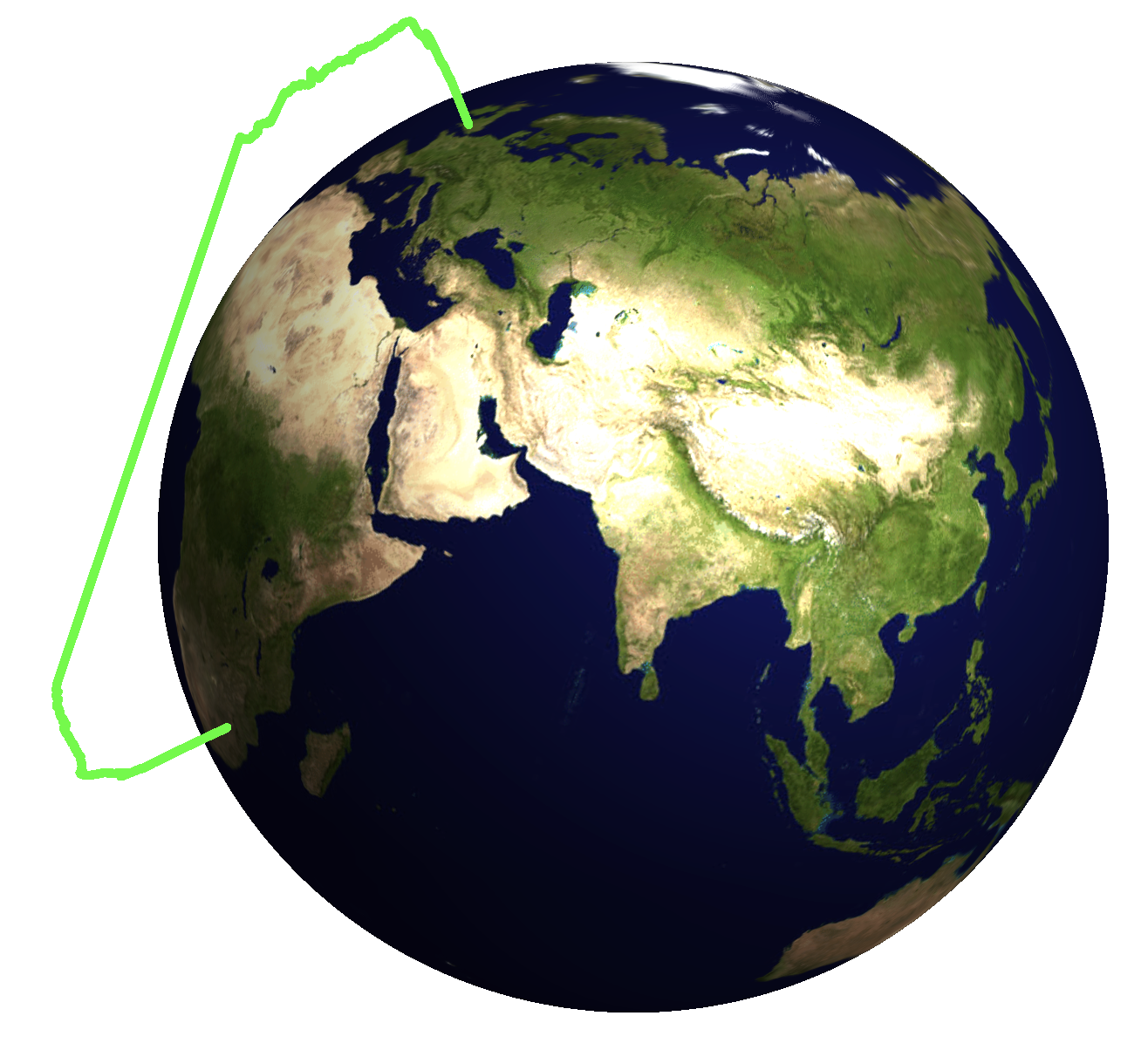
If we want to plot multiple flights we should modify the function slightly.
myFlightPathMulti[data_, radius_, scale_] :=
Show[SphericalPlot3D[radius, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, TextureCoordinateFunction -> ({#5, 1 - #4} &),
PlotStyle -> Directive[Specularity[White, 10], Texture[Import["~/Desktop/backgroundimage.gif"]]],
Lighting -> "Neutral", Axes -> False, RotationAction -> "Clip", Boxed -> False, PlotPoints -> 100,
PlotRange -> {{-3, 3}, {-3, 3}, {-3, 3}}, ImageSize -> Full],
Graphics3D[Flatten[{RandomColor[], Thickness[0.004], Line[(radius + #[[2]]*scale)*#[[1]] & /@
Transpose[{toCoordinates[#[[All, 1]]], lengths[#[[All, 2]]]} &@({#[[1]], 1. #[[2]]} & /@ #)]]}] & /@ data]]
Let's prepare the data.
flightpathsmult =
Join[{{#[[1, 1]], 0.}}, #, {{#[[-1, 1]], 0.}}] & /@ Select[({ToExpression[StringSplit[#[[4]], ","]], #[[6]]} & /@ # & /@ flightdataGXLED[[All, 2 ;;]]), Length[#] > 1 &];
The trajectories seem to come out fine:
Graphics3D[
Flatten[{RandomColor[], Thickness[0.01], Line[(2. + #[[2]]*0.3)*#[[1]] & /@
Transpose[{toCoordinates[#[[All, 1]]], lengths[#[[All, 2]]]} &@({#[[1]], 1. #[[2]]} & /@ #)]]}] & /@ flightpathsmult[[1 ;; 10]]]
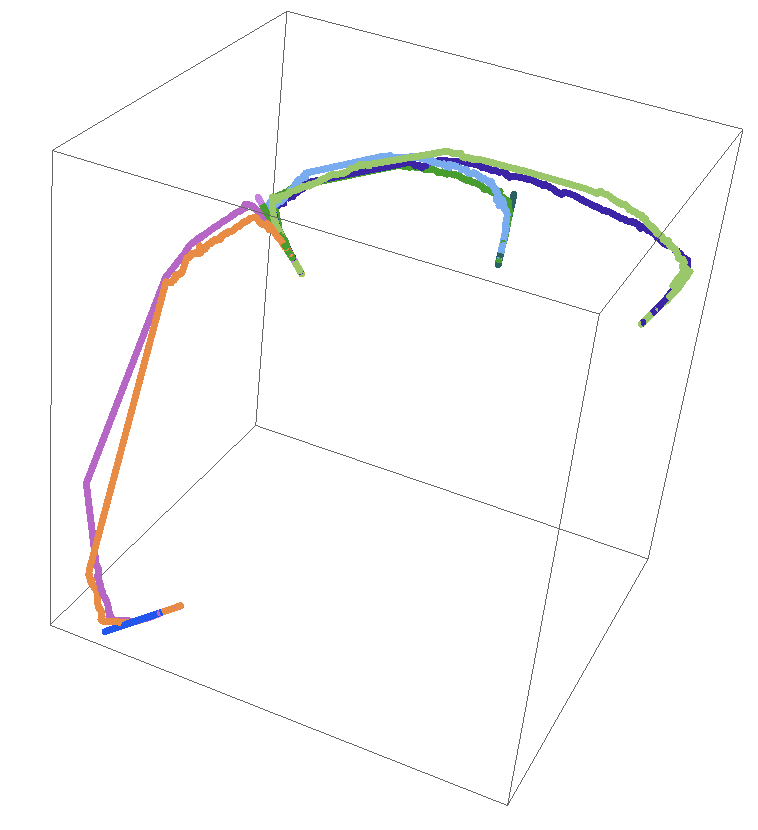
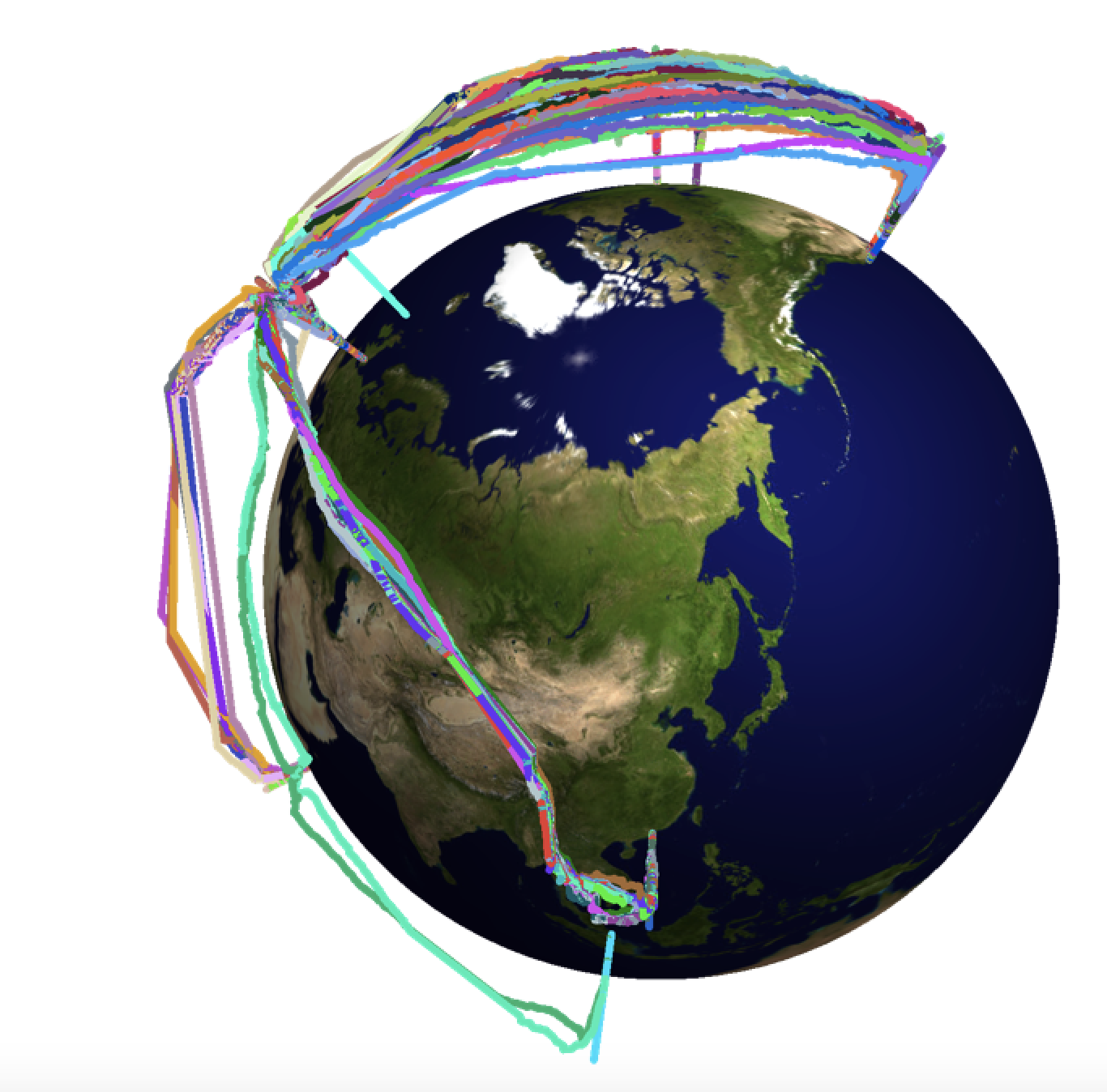
Note, that there are some "straight lines" in the trajectories. They correspond to a lack of data point over unpopulated areas. Plotting all trajectories on the globe looks like this:
myFlightPathMulti[flightpathsmult, 2., 1/3.]
Let's choose a black background:
myFlightPathMultiBlack[data_, radius_, scale_] :=
Show[SphericalPlot3D[radius, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, TextureCoordinateFunction -> ({#5, 1 - #4} &),
PlotStyle -> Directive[Specularity[White, 10], Texture[Import["~/Desktop/backgroundimage.gif"]]],
Lighting -> "Neutral", Axes -> False, RotationAction -> "Clip", Boxed -> False, PlotPoints -> 100,
PlotRange -> {{-3, 3}, {-3, 3}, {-3, 3}}, ImageSize -> Full, Background -> Black],
Graphics3D[Flatten[{RandomColor[], Thickness[0.004], Line[(radius + #[[2]]*scale)*#[[1]] & /@
Transpose[{toCoordinates[#[[All, 1]]], lengths[#[[All, 2]]]} &@({#[[1]], 1. #[[2]]} & /@ #)]]}] & /@ data, Background -> Black]]
and plot:
myFlightPathMultiBlack[flightpathsmult, 2., 1/3.]

This gives the animation at the beginning of this post.
Further Information that we can extract from the data
We can also use the data to get some information about the usage of aeroplanes. We can take the plane with the call sign D-EACB and check for the percentage of time that it is airborne. We first calculate the time window I have data for:
approxTimeWindowDEACB =
Differences[{Select[flightdataDEACB[[1]], #[[-3]] > 10 &][[1, 1]], Select[flightdataDEACB[[Length[flightdataDEACB]]], #[[-3]] > 10 &][[-1, 1]]}][[1]]
This gives 1046462 and is given in seconds. To compute the (approximate) time the plane is airborne we have to check for altitudes larger than some threshold.
approxTimeinAirDEACB =
Total[Flatten[Table[Differences@Reverse@Select[flightdataDEACB[[k]], #[[-3]] > 10 &][[All, 1]][[{1, -1}]], {k, 1, Length[flightdataDEACB]}]]]
which gives 247835 seconds. Now, we can calculate the respective fraction.
N[approxTimeinAirDEACB/approxTimeWindowDEACB]
which gives 0.236831. So this is approximately 24% of the time. Given that planes on short haul flights are mostly grounded over night and that they have substantial time at the airports this seems to be reasonable. Let's do the same for the A 380.
approxTimeWindowGXLED =
Differences[Flatten[Select[Table[Select[Select[flightdataGXLED, Length[#] > 1 &][[k]], #[[-3]] > 10 &], {k, 1, Length[Select[flightdataGXLED, Length[#] > 1 &]]}], Length[#] > 1 &], 1][[{1, -1}, 1]]][[1]]
which is 4258510, and
approxTimeinAirGXLED =
Total[Select[Flatten[Table[If[Length[Select[flightdataGXLED[[k]], #[[-3]] > 10 &][[All, 1]]] > 1,
Differences@Reverse@Select[flightdataGXLED[[k]], #[[-3]] > 10 &][[All, 1]][[{1, -1}]]], {k, 1, Length[flightdataGXLED]}]], NumberQ]]
which is 2445537. This gives
N[approxTimeinAirGXLED/approxTimeWindowGXLED]
so about 57%; hence a more efficient aeroplane use. We can now also determine the average speed when the plane is moving.
N@Mean[DeleteCases[Flatten[flightdataGXLED[[All, 2 ;;]], 1][[All, 6]],0]]
(*366.84*)
This is 367 kts or
UnitConvert[366.84 Quantity[1, "Knots"], Quantity[1, (("Kilometers")/("Hours"))]]
680 km/h. Note that this is a rather inappropriate estimate, because the data is not necessarily sampled uniformly and especially data from over the oceans might be missing. If we accept that issue we can calculate the histogram of the data:
Histogram[DeleteCases[Flatten[flightdataGXLED[[All, 2 ;;]], 1][[All, 6]], 0], Automatic, "PDF", FrameLabel -> {"Speed in kts", "Probablity"},
LabelStyle -> Directive[Bold, 16], ImageSize -> Large, PlotTheme -> "Marketing", ColorFunction -> "TemperatureMap"]
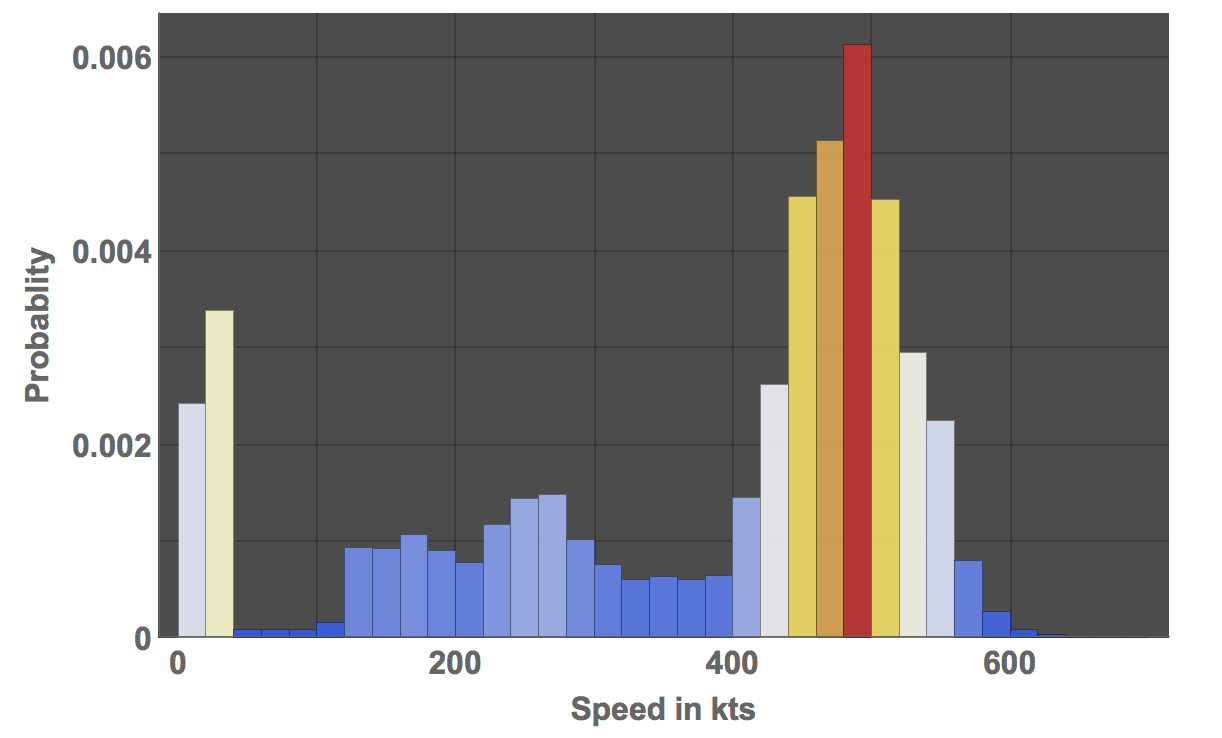
This graphic suggests that the fast speed flight time is vastly underestimated. The maximum speed is
Max@DeleteCases[Flatten[flightdataGXLED[[All, 2 ;;]], 1][[All, 6]], 0]
(*697*)
which is a ground speed of
N@UnitConvert[697 Quantity[1, "Knots"], Quantity[1, (("Kilometers")/("Hours"))]]
1290.84 km.h. We can compare this to the speed of sound in air.
UnitConvert[ThermodynamicData["Air", "SoundSpeed", {"Temperature" -> Quantity[20, "DegreesCelsius"], "Pressure" -> Quantity[1, "Atmospheres"]}], "Kilometers"/"Hours"]
which gives 1236.18 km/h. So the maximum speed is
1290.84/1236.16
104% of the speed of sound, or Mach 1 (at ground level), which is a bit on the high side. Note that the top speed of the A380 is given as 1020 km/h. The peak in the histogram at cruising speed is at around 490 kts which is in fact the maximal speed of the A380 as given in Wikipedia. The higher than expected ground speed might be due to the jet stream - even though speeds of more than Mach 1 seem to be unlikely. There are some reports of this happening though.
This is only a very brief description of what can be achieved with the fantastic data from flightradar24. I encourage everyone to join that community and contribute data. The data provided on that site and the power of the Wolfram Language will allow you to gain insight into what is going on in the skies.
Cheers,
Marco