Introduction

Back in Wolfram Summer School 2016 I worked on the project "Image Transformation with Neural Networks: Real-Time Style Transfer and Super-Resolution", which got later published on Wolfram Community. At the time I had to use the MXNetLink package, but now all the needed functionality is built-in, so here is a top-level implementation of artistic style transfer with Wolfram Language. This is a slightly simplified version of the original method, as it uses a single VGG layer to extract the style features, but a full implementation is of course possible with minor modifications to the code. You can also find this example in the docs:

NetTrain >> Applications >> Computer Vision >> Style Transfer

Code

Create a new image with the content of a given image and in the style of another given image. This implementation follows the method described in Gatys et al., A Neural Algorithm of Artistic Style. An example content and style image:

To create the image which is a mix of both of these images, start by obtaining a pre-trained image classification network:

vggNet = NetModel["VGG-16 Trained on ImageNet Competition Data"];

Take a subnet that will be used as a feature extractor for the style and content images:

featureNet = Take[vggNet, {1, "relu4_1"}]

There are three loss functions used. The first loss ensures that the "content" is similar in the synthesized image and the content image:

contentLoss = NetGraph[{MeanSquaredLossLayer[]}, {1 -> NetPort["LossContent"]}]

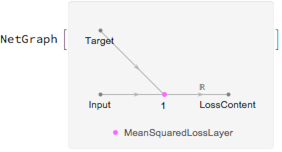
The second loss ensures that the "style" is similar in the synthesized image and the style image. Style similarity is defined as the mean-squared difference between the Gram matrices of the input and target:

gramMatrix = NetGraph[{FlattenLayer[-1], TransposeLayer[1 -> 2],   DotLayer[]}, {1 -> 3, 1 -> 2 -> 3}];

styleLoss = NetGraph[{gramMatrix, gramMatrix, MeanSquaredLossLayer[]},
{NetPort["Input"] -> 1, NetPort["Target"] -> 2, {1, 2} -> 3,  3 -> NetPort["LossStyle"]}]

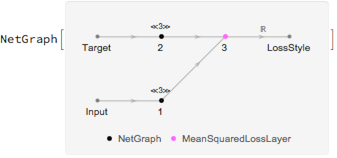
The third loss ensures that the magnitude of intensity changes across adjacent pixels in the synthesized image is small. This helps the synthesized image look more natural:

l2Loss = NetGraph[{ThreadingLayer[(#1 - #2)^2 &], SummationLayer[]}, {{NetPort["Input"], NetPort["Target"]} -> 1 -> 2}];

tvLoss = NetGraph[<|
   "dx1" -> PaddingLayer[{{0, 0}, {1, 0}, {0, 0}}, "Padding" -> "Fixed" ],
   "dx2" ->  PaddingLayer[{{0, 0}, {0, 1}, {0, 0}}, "Padding" -> "Fixed"],
   "dy1" ->  PaddingLayer[{{0, 0}, {0, 0}, {1, 0}}, "Padding" -> "Fixed" ],
   "dy2" ->  PaddingLayer[{{0, 0}, {0, 0}, {0, 1}}, "Padding" -> "Fixed"],
   "lossx" -> l2Loss, "lossy" -> l2Loss, "tot" -> TotalLayer[]|>,
 {{"dx1", "dx2"} -> "lossx", {"dy1", "dy2"} -> "lossy",
   {"lossx", "lossy"} -> "tot" -> NetPort["LossTV"]}]

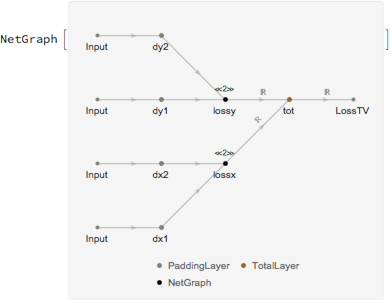
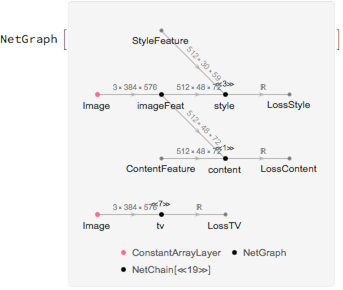
Define a function that creates the final training net for any content and style image. This function also creates a random initial image:

createTransferNet[net_, content_Image, styleFeatSize_] := Module[{dims = Prepend[3]@Reverse@ImageDimensions[content]},
NetGraph[<|
"Image" -> ConstantArrayLayer["Array" -> RandomReal[{-0.1, 0.1}, dims]],
"imageFeat" -> NetReplacePart[net, "Input" -> dims],
"content" -> contentLoss,
"style" -> styleLoss,
"tv" -> tvLoss|>,
{"Image" -> "imageFeat",
{"imageFeat", NetPort["ContentFeature"]} -> "content",
{"imageFeat", NetPort["StyleFeature"]} -> "style",
"Image" -> "tv"},
"StyleFeature" -> styleFeatSize   ] ]

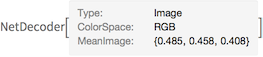
Define a NetDecoder for visualizing the predicted image:

meanIm = NetExtract[featureNet, "Input"][["MeanImage"]]

{0.48502, 0.457957, 0.407604}

decoder = NetDecoder[{"Image", "MeanImage" -> meanIm}]

The training data consists of features extracted from the content and style images. Define a feature extraction function:

extractFeatures[img_] := NetReplacePart[featureNet, "Input" ->NetEncoder[{"Image", ImageDimensions[img], 
 "MeanImage" ->meanIm}]][img];

Create a training set consisting of a single example of a content and style feature:

trainingdata = <|
  "ContentFeature" -> {extractFeatures[contentImg]},
   "StyleFeature" -> {extractFeatures[styleImg]}
  |>

Create the training net whose input dimensions correspond to the content and style image dimensions:

net = createTransferNet[featureNet, contentImg, 
   Dimensions@First@trainingdata["StyleFeature"]];

When training, the three losses are weighted differently to set the relative importance of the content and style. These values might need to be changed with different content and style images. Create a loss specification that defines the final loss as a combination of the three losses:

perPixel = 1/(3*Apply[Times, ImageDimensions[contentImg]]);
lossSpec = {"LossContent" -> Scaled[6.*10^-5], 
   "LossStyle" -> Scaled[0.5*10^-14], 
   "LossTV" -> Scaled[20.*perPixel]};

Optimize the image using NetTrain. LearningRateMultipliers are used to freeze all parameters in the net except for the ConstantArrayLayer. The training is best done on a GPU, as it will take up to an hour to get good results with CPU training. The training can be stopped at any time via Evaluation -> Abort Evaluation:

trainedNet = NetTrain[net,
  trainingdata, lossSpec,
  LearningRateMultipliers -> {"Image" -> 1, _ -> None},
  TrainingProgressReporting -> 
   Function[decoder[#Weights[{"Image", "Array"}]]],
  MaxTrainingRounds -> 300, BatchSize -> 1,
  Method -> {"ADAM", "InitialLearningRate" -> 0.05},
  TargetDevice -> "GPU"
  ]

Extract the final image from the ConstantArrayLayer of the trained net:

decoder[NetExtract[trainedNet, {"Image", "Array"}]]