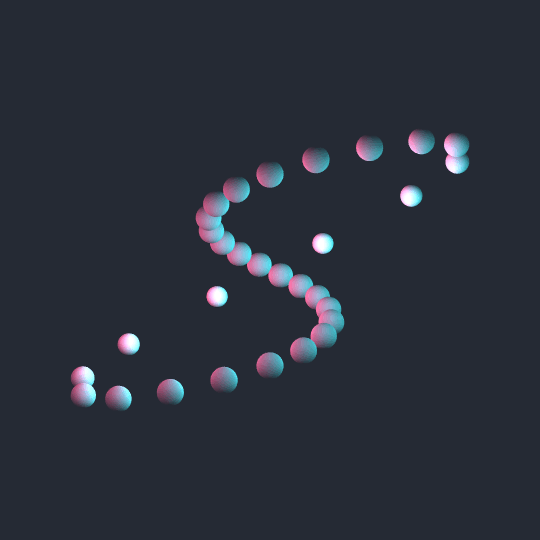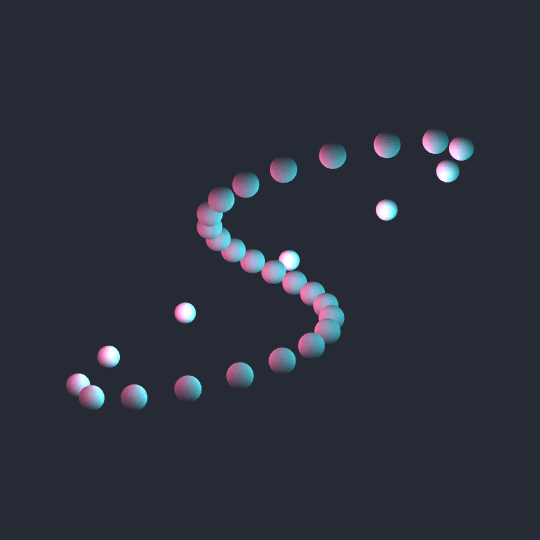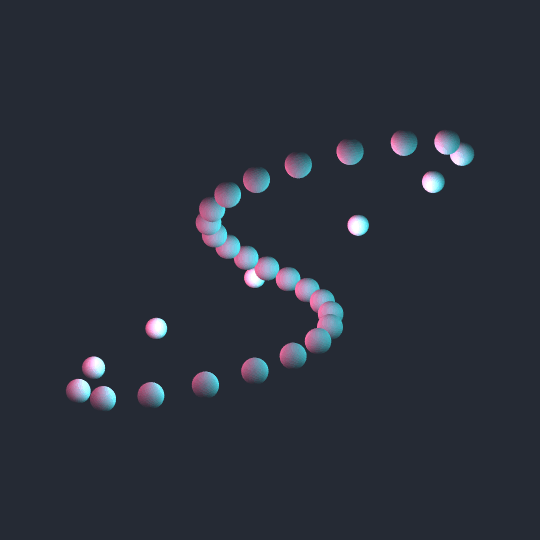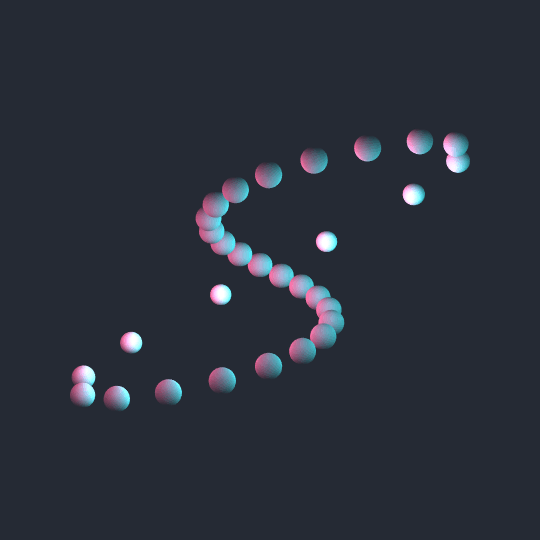
To Infinity
This one is very simple: just a $(2,1)$-torus knot (which of course is topologically an unknot) viewed from straight on (rather than above, which is the more common viewpoint for torus knots). I quite like the blending of colors on the spheres, which was achieved by placing a total of 16 point source lights on a grid in the scene.
The downside of using so many lights in Lighting is that it really slows things down. Just based on quick-and-dirty experimentation, it seems like everything slows to a crawl when you get above about 10 distinct light sources.
That being said, here's code using only 8 point lights (plus one ambient light source) that looks almost the same as the animation and is fast enough to Manipulate reasonably. If you really want to recreate the animation, use d=0.82 rather than d=0.8 and use {j, 0, n, α} rather than {j, 2, n, α}.
Stereo3D[{x1_, y1_, x2_, y2_}] := {x1/(1 - y2), y1/(1 - y2), x2/(1 - y2)};
pqtorus[t_, φ_, p_, q_] := 1/Sqrt[2] {E^(p I (t + φ/p)), E^(q I t)};
With[{viewpoint = {2, 0, 0}, d = .8, n = 3, α = 1, m = 30,
cols = RGBColor /@ {"#08D9D6", "#FF2E63", "#252A34"}},
Manipulate[
Graphics3D[
{Sphere[#, .1] & /@
Table[Stereo3D[Flatten[ReIm /@ pqtorus[t + φ, 0, 2, 1]]], {t, 0., 2 Pi, 2 Pi/m}]},
PlotRange -> 3, ViewPoint -> viewpoint, ViewVertical -> {1, 0, 0},
ViewAngle -> Pi/9, ViewCenter -> {.38, .5, .5}, Boxed -> False,
Background -> cols[[-1]], ImageSize -> 540,
Lighting ->
Append[Flatten[
Table[{"Point", Darker[Blend[Reverse@cols[[;; 2]], i/n], d], {3/2 (j - n/2), 3/2 (i - n/2), 0}},
{i, 0, n, α}, {j, 2, n, α}], 1],
{"Ambient", cols[[-1]], viewpoint}]],
{φ, 0., 2 Pi/m}]
]